贵州省遵义市2021-2022学年八年级上学期期末数学试试卷
试卷更新日期:2022-02-24 类型:期末考试
一、单选题
-
1. 若分式 有意义,则x的取值范围是( )A、 B、 C、 D、2. 三角形的内角和是( )A、60° B、90° C、180° D、360°3. 计算 的结果是( )A、 B、 C、 D、4. 若一个三角形的两条边的长为5和7,那么第三边的长可能是( )A、2 B、10 C、12 D、135. 如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
 A、∠BCA=∠F B、∠B=∠E C、BC∥EF D、∠A=∠EDF6. 若代数式 是一个完全平方式,那么k的值是( )A、1 B、2 C、3 D、47. 已知 , ,则 的值为( )A、8 B、9 C、10 D、128. 已知 的周长是16,且 ,又 ,D为垂足,若 的周长是12,则AD的长为( )A、7 B、6 C、5 D、49. 在计算 通分时,分母确定为( )A、 B、 C、 D、10. 若 , 则 的值是( )
A、∠BCA=∠F B、∠B=∠E C、BC∥EF D、∠A=∠EDF6. 若代数式 是一个完全平方式,那么k的值是( )A、1 B、2 C、3 D、47. 已知 , ,则 的值为( )A、8 B、9 C、10 D、128. 已知 的周长是16,且 ,又 ,D为垂足,若 的周长是12,则AD的长为( )A、7 B、6 C、5 D、49. 在计算 通分时,分母确定为( )A、 B、 C、 D、10. 若 , 则 的值是( )A.1 B. C.2 D.
A、1 B、-1 C、2 D、-211. 点D、E分别是等边三角形 的边 、 的中点, ,F是AD上一动点,则 的最小值是( ) A、6 B、7 C、8 D、912. 若 ,则 的值是( )A、 B、 C、 D、
A、6 B、7 C、8 D、912. 若 ,则 的值是( )A、 B、 C、 D、二、填空题
-
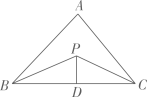
13. 点 关于y轴的对称点 的坐标为.14. 我们要“远离毒品,珍惜生命”,科学研究发现某种毒品的分子直径是 米,则数字 用科学记数法表示为.15. 如图,已知 的周长是22,PB、PC分别平分 和 , 于D,且 , 的面积是.
 16. 平面直角坐标系中有点 、 ,连接AB,以AB为直角边在第一象限内作等腰直角三角形 ,则点C的坐标是.
16. 平面直角坐标系中有点 、 ,连接AB,以AB为直角边在第一象限内作等腰直角三角形 ,则点C的坐标是.三、解答题
-
17.(1)、计算:(2)、解方程:18.(1)、计算:(2)、因式分解:19. 先化简,再求值: ,(其中 ).20. 在棋盘中建立如图所示的平面直角坐标系,A、O、B三颗棋子的位置如图所示,它们的坐标分别是 , , .
 (1)、如图添加棋子C,使A、O、B、C四颗棋子成为一个轴对称图形,请在图中画出该图形的对称轴.(2)、在其他格点(除点C外)位置添加一颗棋子P,使A、O、B、P四颗棋子成为一个轴对称图形,直接写出棋子P的位置坐标(写出2个即可).21. 如图:点E、F在BC上, , , ,AF与DE交于点G.过点G作 ,垂足为H.
(1)、如图添加棋子C,使A、O、B、C四颗棋子成为一个轴对称图形,请在图中画出该图形的对称轴.(2)、在其他格点(除点C外)位置添加一颗棋子P,使A、O、B、P四颗棋子成为一个轴对称图形,直接写出棋子P的位置坐标(写出2个即可).21. 如图:点E、F在BC上, , , ,AF与DE交于点G.过点G作 ,垂足为H.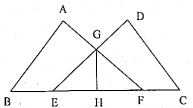 (1)、求证:(2)、求证:22. 如图: ,点P是 角平分线上一点,过点P作PC平行OA交OB于点C, 于点D,若 .
(1)、求证:(2)、求证:22. 如图: ,点P是 角平分线上一点,过点P作PC平行OA交OB于点C, 于点D,若 .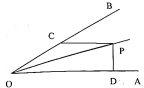 (1)、求证: 是等腰三角形.(2)、求 的长.23. 在2021年10月,遵义市汇川区确诊一例有甘肃等旅居史的新冠肺炎患者,疫情期间,某校根据政府防控要求用4000元购买了一批口罩,两天后,学校后勤人员发现口罩数量不多了,学校决定再次用5000元购买一批口罩作为备用,后勤人员发现这时每只口罩价格涨了 元,结果两次购买口罩的数量相同.(1)、学校两次购买口罩的单价分别是多少元?(2)、学校两次共购买口罩多少只?24. 在边长为8的等边三角形 中,点Q是BC上一点,点P是AB上一动点,点P以1个单位每秒的速度从点A向点B移动,设运动时间为t秒.
(1)、求证: 是等腰三角形.(2)、求 的长.23. 在2021年10月,遵义市汇川区确诊一例有甘肃等旅居史的新冠肺炎患者,疫情期间,某校根据政府防控要求用4000元购买了一批口罩,两天后,学校后勤人员发现口罩数量不多了,学校决定再次用5000元购买一批口罩作为备用,后勤人员发现这时每只口罩价格涨了 元,结果两次购买口罩的数量相同.(1)、学校两次购买口罩的单价分别是多少元?(2)、学校两次共购买口罩多少只?24. 在边长为8的等边三角形 中,点Q是BC上一点,点P是AB上一动点,点P以1个单位每秒的速度从点A向点B移动,设运动时间为t秒.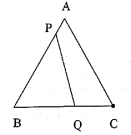
 (1)、如图1,若 ,当t取何值时 ?(2)、若点P从点A向点B运动,同时点Q以2个单位的速度从点B经点C向点A运动,当t为何值时, 为等边三角形(在图2中画出示意图).(3)、如图3,将边长为 的等边三角形 变换为AB,AC为腰,BC为底的等腰三角形,且 , ,点P运动到AB中点处静止后,点M,N分别为BC,AC上动点,点M以1个单位每秒的速度从点B向C运动,同时点N以a个单位每秒的速度从点C向A运动,当 , 全等时,直接写出a的值.
(1)、如图1,若 ,当t取何值时 ?(2)、若点P从点A向点B运动,同时点Q以2个单位的速度从点B经点C向点A运动,当t为何值时, 为等边三角形(在图2中画出示意图).(3)、如图3,将边长为 的等边三角形 变换为AB,AC为腰,BC为底的等腰三角形,且 , ,点P运动到AB中点处静止后,点M,N分别为BC,AC上动点,点M以1个单位每秒的速度从点B向C运动,同时点N以a个单位每秒的速度从点C向A运动,当 , 全等时,直接写出a的值.