贵州省铜仁市松桃苗族自治县2021-2022学年八年级上学期期末数学试卷

试卷更新日期：2022-02-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $\sqrt{{(\pm 2)}^{2}} = \pm 2$ C、 ${(\sqrt{2})}^{2} = 2$ D、 ${(- \sqrt{2})}^{2} = - 2$

查看试题解析
2. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片，该芯片的制造工艺达到了0.000000022米.用科学记数法表示0.000000022为（）

A、22×10^﹣10 B、2.2×10^﹣10 C、2.2×10^﹣9 D、2.2×10^﹣8

查看试题解析
3. 下列命题是真命题的个数为（）
①一个角的补角大于这个角.②三角形的内角和是180°.③若 $a^{2} = b^{2}$ ，则 $a = b$ .④相等的角是对顶角.⑤两点之间，线段最短.

A、2 B、3 C、4 D、5

查看试题解析
4. 使分式 $\frac{x^{2} - 1}{x + 1}$ 等于0的x的值是（）

A、1 B、 $- 1$ C、 $\pm 1$ D、不存在

查看试题解析
5. 人字梯中间一般会设计一“拉杆”，这样做的道理是（）

A、两点之间线段最短 B、三角形的稳定性 C、两点确定一条直线 D、垂线段最短

查看试题解析
6. 不等式 $\frac{x}{3} - \frac{x - 1}{2} \geq 1$ 的最大整数解是（）

A、0 B、 $- 1$ C、 $- 2$ D、 $- 3$

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ，AE是 $△ A B C$ 的外角 $∠ B A D$ 的平分线，BF平分 $∠ A B C$ 与AE的反向延长线相交于点F，则 $∠ B F E$ 为（）

A、35° B、40° C、45° D、50°

查看试题解析
8. 若关于x的分式方程 $\frac{x - 3}{x - 1} = \frac{m}{x - 1} + 2$ 产生增根，则m的值为（）

A、 $- 1$ B、 $- 2$ C、1 D、2

查看试题解析
9. 如图，△ABC是等边三角形，点E是AC的中点，过点E作EF⊥AB于点F，延长BC交EF的反向延长线于点D，若EF=1，则DF的长为（）

A、2 B、2.5 C、3 D、3.5

查看试题解析
10. 随着科技的进步，在很多城市都可以通过手机APP实时查看公交车到站情况.小聪同学想乘公交车，他走到A、B两站之间的C处，拿出手机查看了公交车到站情况，发现他与公交车的距离为700m（如图），此时他有两种选择：
①与公交车相向而行，到A公交站去乘车；
②与公交车同向而行，到B公交站去乘车.
假设公交车的速度是小聪速度的6倍，小聪无论选择哪站乘坐都不会错过这辆公交车，则A，B两公交站之间的距离最大为（）

A、240m B、260m C、280m D、300m

查看试题解析

二、填空题

11. 代数式 $\frac{\sqrt{x}}{x - 2}$ 有意义时，x应满足的条件为.

查看试题解析
12. 若 $x > y$ ，则 $3 - 5 x$ $3 - 5 y$ （填“＞”或“＝”或“＜”）.

查看试题解析
13. 若a，b为等腰 $△ A B C$ 的两边，且满足 $| a - 2 | + \sqrt{b - 4} = 0$ ，则 $△ A B C$ 的周长为.

查看试题解析
14. 如图，在等边三角形ABC中， $∠ A B C$ 的平分线与 $∠ A C B$ 的平分线相交于D，过点D作 $E F ∥ B C$ 交AB于E，交AC于F， $E F = 4$ ，则BC的长为.

查看试题解析
15. 观察数据并寻找规律： $\sqrt{2}$ ， $- 2$ ， $\sqrt{6}$ ， $- 2 \sqrt{2}$ ， $\sqrt{10}$ ……，则第2021个数是.

查看试题解析
16. 如图，在 △ABC 中，BE平分 ∠ABC ， AE⊥BE 于点E， △BCE 的面积为2，则 △ABC 的面积是.

查看试题解析

三、解答题

17. 计算：

(1)、 ${(\frac{1}{3})}^{- 2} - {(2 \sqrt{3})}^{2} + {(π - 3.14)}^{0} - \sqrt[3]{- 8}$ ；

(2)、 ${(\sqrt{6} - \sqrt{3})}^{2} + 6 \sqrt{\frac{2}{3}} \times \sqrt{3}$ .

查看试题解析
18. 先化简，再求值： $(\frac{x + 1}{x - 1} + \frac{1}{x^{2} - 2 x + 1}) \div \frac{x}{x - 1}$ ，然后从 $- 1 \leq x \leq 1$ 中，选择一个合适的整数作为x的值代入求值.

查看试题解析
19. 解分式方程： $\frac{1 - x}{x - 2} + 2 = \frac{1}{2 - x}$ ．

查看试题解析
20. 如图①： $△ A B C$ 中， $A C = B C$ ，延长AC到E，过点E作 $E F ⊥ A B$ 交AB的延长线于点F，延长CB到G，过点G作 $G H ⊥ A B$ 交AB的延长线于H，且 $E F = G H$ .

(1)、求证： $△ A E F$ ≌ $△ B G H$ ；

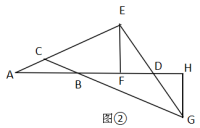(2)、如图②，连接EG与FH相交于点D，若 $A B = 4$ ，求DH的长.

查看试题解析
21. 先阅读下列材料，再解决问题：
阅读材料：数学上有一种根号内又带根号的数，它们能通过完全平方公式及二次根式的性质化去一层根号.

例如： $\sqrt{3 + 2 \sqrt{2}} = \sqrt{3 + 2 \times 1 \times \sqrt{2}} = \sqrt{1^{2} + 2 \times 1 \times \sqrt{2} + {(\sqrt{2})}^{2}}$

$= \sqrt{{(1 + \sqrt{2})}^{2}} = | 1 + \sqrt{2} | = 1 + \sqrt{2}$ .

解决问题：化简下列各式

(1)、 $\sqrt{7 + 4 \sqrt{3}}$ ；

(2)、 $\sqrt{9 - 4 \sqrt{5}}$ .

查看试题解析
22. 如图，在 $△ A B C$ 中， $∠ B A C = 30 °$ ，AB边的垂直平分线分别交AB于点E，交AC于点F，点D在EF上，且 $B D = C D$ ，G是AC的中点，连接DG.

(1)、求证： $D G ⊥ A C$ ；

(2)、判断 $△ B C D$ 是否是等边三角形，并说明理由.

查看试题解析
23. 生活垃圾处理是关系民生的基础性公益事业，加强生活垃圾分类处理，维护公共环境和节约资源是全社会共同的责任，某小区准备购进A型和B型两种垃圾桶，已知购买一个B型垃圾桶比购买一个A型垃圾桶多花20元，用250元购进A型垃圾桶的数量与用350元购进B型垃圾桶的数量相等.

(1)、求购买一个A型垃圾桶、一个B型垃圾桶各需多少元？

(2)、小区决定用不超过600元购进A、B两种型号的垃圾桶共10台，且A型垃圾桶的个数不多于B型垃圾桶的个数的2倍，问小区有几种购买方案？

查看试题解析
24. 在等边三角形ABC中，点D是BC的中点， $∠ E D F = 120 °$ ， $∠ E D F$ 的两边分别交直线AB，AC于点E，F.

(1)、问题发现：如图①，当点E，F分别在线段AB，AC上，且 $D E ⊥ A B$ ， $D F ⊥ A C$ 时，请直接写出线段DE与DF的数量关系：；

(2)、类比探究：如图②，当点E落在线段AB上，点F落在射线AC上时，（1）中的结论是否仍然成立？请结合图②说明理由：

(3)、拓展应用：如图③，当点E落在射线BA上，点F落在射线AC上时，若 $A E = 2$ ， $C F = 4$ ，请求出AB.

查看试题解析