贵州省毕节市2021-2022学年八年级上学期期末数学试卷
试卷更新日期:2022-02-24 类型:期末考试
一、单选题
-
1. 的算术平方根是( )A、 B、4 C、 D、22. 下列各图给出了变量x与y之间的对应关系,其中y是x的函数的是( )A、
 B、
B、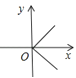 C、
C、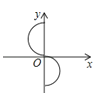 D、
D、 3. 若一组数据7,15,10,5,x,20的平均数是10,则这组数据的极差是( )A、10 B、13 C、15 D、174. 函数y= 中,自变量x的取值范围是( )A、x≤5 B、x<5 C、x≥5 D、x>55. 如图,已知点B、C、D在同一直线上, , ,则 ( )
3. 若一组数据7,15,10,5,x,20的平均数是10,则这组数据的极差是( )A、10 B、13 C、15 D、174. 函数y= 中,自变量x的取值范围是( )A、x≤5 B、x<5 C、x≥5 D、x>55. 如图,已知点B、C、D在同一直线上, , ,则 ( )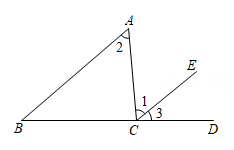 A、42° B、45° C、48° D、无法确定6. 已知点 在x轴上,点 在y轴上,则点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 下列计算正确的是( )A、 B、 C、 D、8. 直线 经过二、三、四象限,则直线 的图象只能是图中的( )A、
A、42° B、45° C、48° D、无法确定6. 已知点 在x轴上,点 在y轴上,则点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 下列计算正确的是( )A、 B、 C、 D、8. 直线 经过二、三、四象限,则直线 的图象只能是图中的( )A、 B、
B、 C、
C、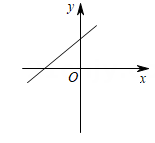 D、
D、 9. 下列命题中,是真命题的有( )
9. 下列命题中,是真命题的有( )①以1、 、 为边的三角形是直角三角形,则1、 、 是一组勾股数;
②若一直角三角形的两边长分别是5、12,则第三边长为13;
③二次根式 是最简二次根式;
④在实数0,﹣0.3333……, ,0.020020002, ,0.23456…, 中,无理数有3个;
⑤东经113°,北纬35.3°能确定物体的位置.
A、①②③④⑤ B、①②④⑤ C、②④⑤ D、④⑤10. 如图所示,一次函数 的图象经过点 ,则方程 的解是( ) A、 B、 C、 D、无法确定11. 已知 的三边分别为a、b、c,且 ,则 的面积为( )A、30 B、60 C、65 D、无法计算12. 在同一平面直角坐标系中,函数 的图象与函数 的图象互相平行,则下列各点在函数 的图象上的点是( )A、 B、 C、 D、13. 如图,在平面直角坐标系中, , ,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,点C表示的实数介于( )
A、 B、 C、 D、无法确定11. 已知 的三边分别为a、b、c,且 ,则 的面积为( )A、30 B、60 C、65 D、无法计算12. 在同一平面直角坐标系中,函数 的图象与函数 的图象互相平行,则下列各点在函数 的图象上的点是( )A、 B、 C、 D、13. 如图,在平面直角坐标系中, , ,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,点C表示的实数介于( ) A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间14. 若关于x、y的二元一次方程 的解,也是方程 的解,则m的值为( )A、-3 B、-2 C、2 D、无法计算15. 如图,元旦期间,某移动公司推出两种不同的收费标准:A种方式是月租20元,B种方式是月租0元,一个月本地网内打出时间t(分)与打出电话费s(元)的函数关系图象,当打出200分钟时,这两种方式的电话费相差( )
A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间14. 若关于x、y的二元一次方程 的解,也是方程 的解,则m的值为( )A、-3 B、-2 C、2 D、无法计算15. 如图,元旦期间,某移动公司推出两种不同的收费标准:A种方式是月租20元,B种方式是月租0元,一个月本地网内打出时间t(分)与打出电话费s(元)的函数关系图象,当打出200分钟时,这两种方式的电话费相差( ) A、15元 B、20元 C、25元 D、30元
A、15元 B、20元 C、25元 D、30元二、填空题
-
16. 某班甲、乙两个同学在5次模拟测试中,数学的平均成绩都是142分,方差分别是 , .在甲、乙两人中,成绩较稳定的是.17. 已知函数 是关于x的一次函数,则 .18. 如图,已知 中, ,BD平分 ,AD平分外角 ,则 度.
 19. 已知一个数的两个平方根分别是 和 ,则这个数的立方根是.20. 如图,在平面直角坐标系中,长方形AOBC的边OB、OA分别在x轴、y轴上,点D在边BC上,将该长方形沿AD折叠,点C恰好落在边OB上的E处.若点 ,点 ,则点D的坐标是.
19. 已知一个数的两个平方根分别是 和 ,则这个数的立方根是.20. 如图,在平面直角坐标系中,长方形AOBC的边OB、OA分别在x轴、y轴上,点D在边BC上,将该长方形沿AD折叠,点C恰好落在边OB上的E处.若点 ,点 ,则点D的坐标是.
三、解答题
-
21. 计算(1)、(2)、22. 解下列方程组(1)、 . (代入消元法)(2)、 (加减消元法)23. “双减”落实后,某校抽查了50名八年级学生的睡眠时间.并将统计结果绘制成了统计图.请根据图中的信息解答下列问题:
 (1)、该组数据的众数是 , 中位数是;(2)、求这50名学生的平均睡眠时间是多少小时?(保留整数)(3)、根据样本数据,估计该校八年级每位学生的睡眠时间是多少小时?24. 如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 , ,
(1)、该组数据的众数是 , 中位数是;(2)、求这50名学生的平均睡眠时间是多少小时?(保留整数)(3)、根据样本数据,估计该校八年级每位学生的睡眠时间是多少小时?24. 如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 , ,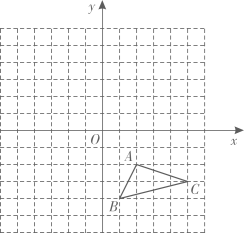 (1)、将 向上平移6个单位长度得到 ,请画出 ;(2)、请画出与 关于y轴对称的 ;(3)、请写出点 、 的坐标.25. 已知:如图,点D、E、F、G都在 的边上, ,且
(1)、将 向上平移6个单位长度得到 ,请画出 ;(2)、请画出与 关于y轴对称的 ;(3)、请写出点 、 的坐标.25. 已知:如图,点D、E、F、G都在 的边上, ,且 (1)、求证: ;(2)、若EF平分 , ,求 的度数.26. 为巩固拓展脱贫攻坚成果,开启乡村振兴发展之门,某村村民组长组织村民加工板栗并进行销售.根据现有的原材料,预计加工规格相同的普通板栗、精品板栗共4000件.某天上午的销售件数和所卖金额统计如下表:
(1)、求证: ;(2)、若EF平分 , ,求 的度数.26. 为巩固拓展脱贫攻坚成果,开启乡村振兴发展之门,某村村民组长组织村民加工板栗并进行销售.根据现有的原材料,预计加工规格相同的普通板栗、精品板栗共4000件.某天上午的销售件数和所卖金额统计如下表:普通板栗(件)
精品板栗(件)
总金额(元)
甲购买情况
2
3
350
乙购买情况
4
1
300
(1)、求普通板栗和精品板栗的单价分别是多少元.(2)、根据(1)中求出的单价,若普通板栗和精品板栗每件的成本分别为40元、60元,且加工普通板栗a件( ),则4000件板栗的销售总利润为w元.问普通板栗和精品板栗各加工多少件,所获总利润最多?最多总利润是多少?27. 如图,正比例函数 的图象与一次函数 的图象交于点 ,一次函数图象经过点 ,与y轴的交点为D,与x轴的交点为C.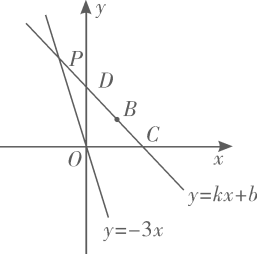 (1)、求一次函数表达式;(2)、求D点的坐标;(3)、求 的面积.(4)、不解关于x、y的方程组 ,直接写出方程组的解.
(1)、求一次函数表达式;(2)、求D点的坐标;(3)、求 的面积.(4)、不解关于x、y的方程组 ,直接写出方程组的解.