四川省眉山市青神县2021-2022学年七年级上学期期末数学试卷
试卷更新日期:2022-02-24 类型:期末考试
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 柳州市大力发展新能源汽车业,仅今年二月宏光MINIEV销量就达17000辆,用科学记数法将数据17000表示为( )A、 B、 C、 D、3. 一个两位数,个位上的数字是a,十位上的数字是b,用代数式表示这个两位数是( )A、ab B、ba C、10a+b D、10b+a4. 下列合并同类项正确的是( )A、 B、 C、 D、5. 在下面的四个几何体中,同一几何体的主视图与俯视图相同的是( )A、
 B、
B、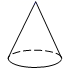 C、
C、 D、
D、 6. 下列各式中,与多项式 相等的是( )A、 B、 C、 D、7. 已知 , ,则 和 的值分别为( )A、-8和32 B、8和32 C、-8和-32 D、8和-328. 如图,在 中, , 平分 ,则 的度数为( )
6. 下列各式中,与多项式 相等的是( )A、 B、 C、 D、7. 已知 , ,则 和 的值分别为( )A、-8和32 B、8和32 C、-8和-32 D、8和-328. 如图,在 中, , 平分 ,则 的度数为( ) A、 B、 C、 D、9. 下列四种说法中,正确的是( )A、几个有理数相乘,同号得正,异号得负 B、任何数的偶次方都是正数 C、 是三次三项式 D、 的系数是 ,次数是310. 如图,点 在直线 上, .若 ,则 的大小为( )
A、 B、 C、 D、9. 下列四种说法中,正确的是( )A、几个有理数相乘,同号得正,异号得负 B、任何数的偶次方都是正数 C、 是三次三项式 D、 的系数是 ,次数是310. 如图,点 在直线 上, .若 ,则 的大小为( )
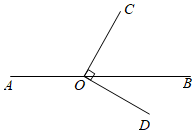 A、 B、 C、 D、11. 如图,AB∥CD∥EF,若∠ABC=130°,∠BCE=55°,则∠CEF的度数为( )
A、 B、 C、 D、11. 如图,AB∥CD∥EF,若∠ABC=130°,∠BCE=55°,则∠CEF的度数为( )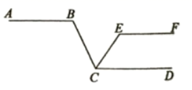 A、95° B、105° C、110° D、115°12. 按规律排列的一组数据: , ,□, , , ,…,其中□内应填的数是( )A、 B、 C、 D、
A、95° B、105° C、110° D、115°12. 按规律排列的一组数据: , ,□, , , ,…,其中□内应填的数是( )A、 B、 C、 D、二、填空题
-
13. 计算:(-1)2022=.14. 如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“迎”字一面的相对面上的字是.
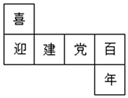 15. 如果∠α是直角的 ,则∠α的补角是度.16. 长方形的一边等于 ,另一边是 ,则这个长方形的周长是.17. 当 时,多项式 与 的和是.18. 实数 , 在数轴上对应的点的位置如图所示,则|a-b|-|b+a|=.
15. 如果∠α是直角的 ,则∠α的补角是度.16. 长方形的一边等于 ,另一边是 ,则这个长方形的周长是.17. 当 时,多项式 与 的和是.18. 实数 , 在数轴上对应的点的位置如图所示,则|a-b|-|b+a|=.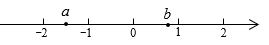 19. 将含30°角的三角板如图摆放,AB CD,若 =20°,则 的度数是.
19. 将含30°角的三角板如图摆放,AB CD,若 =20°,则 的度数是. 20. 下列各正方形中的四个数之间都有相同的规律,根据此规律,x的值为.
20. 下列各正方形中的四个数之间都有相同的规律,根据此规律,x的值为.
三、解答题
-
21.22.23.24.25. 先化简,再求值: ,其中 , .26. 如图,在方格纸中,每个小正方形的边长为一个长度单位,点A、B、C都在格点上.
 (1)、画出线段BC;(2)、将线段BC向上平移三个单位,得到线段DE,在图中画出线段DE;(3)、三角形ADE的面积= .27. 如图,AB与EF交于点B,CD与EF交于点D,根据图形,请补全下面这道题的解答过程.
(1)、画出线段BC;(2)、将线段BC向上平移三个单位,得到线段DE,在图中画出线段DE;(3)、三角形ADE的面积= .27. 如图,AB与EF交于点B,CD与EF交于点D,根据图形,请补全下面这道题的解答过程. (1)、∵∠1=∠2(已知)
(1)、∵∠1=∠2(已知)∴ CD()
∴∠ABD+∠CDB = ()
(2)、∵∠BAC =65°,∠ACD=115°,( 已知 )∴∠BAC+∠ACD=180° (等式性质)
∴AB CD ()
(3)、∵CD⊥AB于D,EF⊥AB于F,∠BAC=55°(已知)∴∠ABD=∠CDF=90°( 垂直的定义)
∴ (同位角相等,两直线平行)
又∵∠BAC=55°,(已知)
∴∠ACD = ( )
28. 已知:如图,AB CD EF,点G、H、M分别在AB、CD、EF上.求证: . 29. A、B两地果园分别有苹果30吨和40吨,C、D两地分别需要苹果20吨和50吨.已知从A地、B地到C地、D地的运价如下表:
29. A、B两地果园分别有苹果30吨和40吨,C、D两地分别需要苹果20吨和50吨.已知从A地、B地到C地、D地的运价如下表:到C地
到D地
从A地果园运出
每吨15元
每吨9元
从B地果园运出
每吨10元
每吨12元
(1)、若从A地果园运到C地的苹果为10吨,则从A地果园运到D地的苹果为吨,从B地果园运到C地的苹果为 吨,从B地果园运到D地的苹果为吨,总运输费用为元.(2)、若从A地果园运到C地的苹果为x吨,求从A、B两地将苹果运到C、D两地的运输总费用.(3)、能否设计一个运输方案,使得运费最少?如果能,请你写出你的方案,最少运费是多少?30. 观察下列等式:,将以上三个等式两边分别相加得: .
(1)、猜想并写出: ;(2)、 ;(3)、 .