河南省洛阳市嵩县2021-2022学年七年级上学期期末考试数学试卷
试卷更新日期:2022-02-24 类型:期末考试
一、单选题
-
1. 一个数的倒数是 ,则这个数是( )A、 B、 C、 D、22. 如图摆放的下列几何体中,左视图是圆的是( )A、
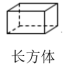 B、
B、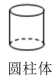 C、
C、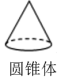 D、
D、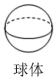 3. 如图,正方体的6个面上分别标有字母A,B,C,D,E,F,将该正方体按图示方式转动,根据图形可得,与字母F相对的是( )
3. 如图,正方体的6个面上分别标有字母A,B,C,D,E,F,将该正方体按图示方式转动,根据图形可得,与字母F相对的是( ) A、字母A B、字母B C、字母C D、字母E4.
A、字母A B、字母B C、字母C D、字母E4.如图,左面的平面图形绕轴旋转一周,可以得到的立体图形是( )
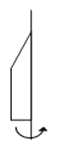 A、
A、 B、
B、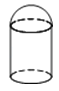 C、
C、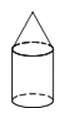 D、
D、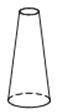 5. 周末小华从家出发,骑车去位于家南偏东35°方位的公园游玩,那么他准备回家时,他家位于公园的哪个方位( )A、北偏西55° B、北偏西35° C、南偏东55° D、南偏西35°6. 丁丁做了 道计算题:① ;② ;③ ;④ .请你帮他检查一下,他一共做对了( )A、 道 B、 道 C、 道 D、 道7. 若当 时, ,则当 时,多项式 的值为( )A、 B、 C、 D、8. 如图,在长方形 纸片中, , ,把纸片沿 折叠后,点 、 分别落在 、 的位置.若 ,则 等于( )
5. 周末小华从家出发,骑车去位于家南偏东35°方位的公园游玩,那么他准备回家时,他家位于公园的哪个方位( )A、北偏西55° B、北偏西35° C、南偏东55° D、南偏西35°6. 丁丁做了 道计算题:① ;② ;③ ;④ .请你帮他检查一下,他一共做对了( )A、 道 B、 道 C、 道 D、 道7. 若当 时, ,则当 时,多项式 的值为( )A、 B、 C、 D、8. 如图,在长方形 纸片中, , ,把纸片沿 折叠后,点 、 分别落在 、 的位置.若 ,则 等于( )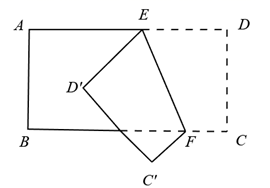 A、70° B、65° C、50° D、25°9. 计算 的值为( )A、 B、 C、 D、10. 如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )
A、70° B、65° C、50° D、25°9. 计算 的值为( )A、 B、 C、 D、10. 如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )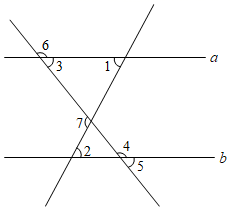 A、3个 B、4个 C、5个 D、6个
A、3个 B、4个 C、5个 D、6个二、填空题
-
11. 的相反数是.12. 七年级举行一次数学基本功大赛,某班 人全部参加,有 人获得一等奖, 人获得二等奖, 人获得三等奖,该班没有获得奖项的同学有人.(用含 、 的代数式表示)13. 将两个三角尺的直角顶点重合为如图所示的位置,若 ,则 .
 14. 生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD=°.
14. 生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD=°.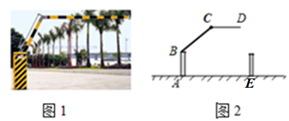 15. 如图, , 的平分线交 于点 , 是 上的一点, 的平分线交 于点 ,且 ,下列结论:
15. 如图, , 的平分线交 于点 , 是 上的一点, 的平分线交 于点 ,且 ,下列结论:① 平分 ;
② ;
③与 互余的角有 个;
④若 ,则 .
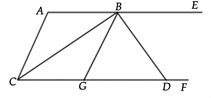
其中正确的是.(请把正确结论的序号都填上)
三、解答题
-
16. 如图,在数轴上有 、 、 这三个点.
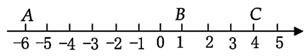
回答:(1)、 、 、 这三个点表示的数各是多少?:; :; :;
(2)、 、 两点间的距离是 , 、 两点间的距离是;(3)、应怎样移动点 的位置,使点 到点 和点 的距离相等?17. 如图,小海龟(头朝上)位于图中点 处,按下述口令移动:前进 格;向右转 ,前进 格;向左转 ,前进 格;向左转 ,前进 格;向右转 ,后退 格;最后向右转 ,前进 格;用粗线将小海龟经过的路线描出来,看一看是什么图形. 18. 如图,已知线段 长 ,点 、 、 、 顺次在 上,且 , 是 的中点, ,求 的长.
18. 如图,已知线段 长 ,点 、 、 、 顺次在 上,且 , 是 的中点, ,求 的长.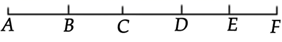 19. 国庆期间,云南即将进入旅游高峰,防疫不可忽视,为了满足景点对口罩的需求,某厂决定生产A、B两种款式的口罩,每天两种口罩的生产量共500包,两种口罩的成本和售价如下表:
19. 国庆期间,云南即将进入旅游高峰,防疫不可忽视,为了满足景点对口罩的需求,某厂决定生产A、B两种款式的口罩,每天两种口罩的生产量共500包,两种口罩的成本和售价如下表:口罩
成本(元/包)
售价(元/包)
A
5
8
B
7
9
设每天生产A种口罩x包.
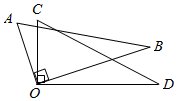
(1)、用含x的代数式表示该工厂每天的生产成本,并化简;(2)、当 时,求该工厂每天获得的利润.20. 补全下列推理过程:如图, , , ,试说明 .
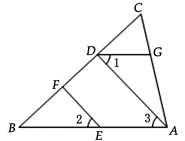
解: , (已知),
(垂直的定义).
( ).
( ).
(已知),
(等量代换).
( ).
21. 已知 , .(1)、当 时,求代数式 的值;(2)、试判断 、 的大小关系,并说明理由.22. 已知一角的两边与另一个角的两边分别平行,试探索这两个角之间的关系,并说明你的结论.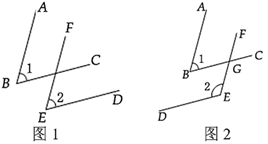 (1)、如图1所示, , ,则 与 的关系是;(2)、如图2所示, , ,则 与 的关系是 ;(3)、经过上述探索,我们可以得到一个结论(试用文字语言表述): ;(4)、若两个角的两边分别平行,且一个角比另一个角的 倍少 ,则这两个分别是多少度?23. 图1展示了光线反射定律:EF是镜面AB的垂线,一束光线m射到平面镜AB上,被AB反射后的光线为n,则入射光线m,反射光线n与垂线EF所夹的锐角 .
(1)、如图1所示, , ,则 与 的关系是;(2)、如图2所示, , ,则 与 的关系是 ;(3)、经过上述探索,我们可以得到一个结论(试用文字语言表述): ;(4)、若两个角的两边分别平行,且一个角比另一个角的 倍少 ,则这两个分别是多少度?23. 图1展示了光线反射定律:EF是镜面AB的垂线,一束光线m射到平面镜AB上,被AB反射后的光线为n,则入射光线m,反射光线n与垂线EF所夹的锐角 .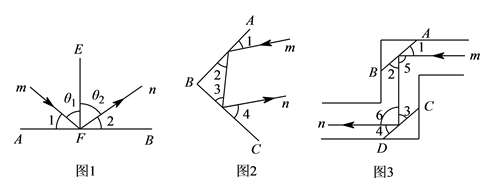 (1)、在图1中,证明:∠1=∠2.(2)、图2中,AB,BC是平面镜,入射光线m经过两次反射后得到反射光线n,已知 , ,判断直线m与直线n的位置关系,并说明理由.(3)、图3是潜望镜工作原理示意图,AB,CD是平行放置的两面平面镜.请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的?
(1)、在图1中,证明:∠1=∠2.(2)、图2中,AB,BC是平面镜,入射光线m经过两次反射后得到反射光线n,已知 , ,判断直线m与直线n的位置关系,并说明理由.(3)、图3是潜望镜工作原理示意图,AB,CD是平行放置的两面平面镜.请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的?