四川省遂宁市2021-2022学年高三上学期理数第一次诊断性考试试卷

试卷更新日期：2022-02-24 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合 $M = {x | x^{2} - 6 x + 5 < 0}$ ， $N = {x | \frac{1}{2} \leq x \leq 3}$ 则 $M \cap N$ 等于（）

A、 ${x | \frac{1}{2} \leq x < 1}$ B、 ${x | 1 < x \leq 3}$ C、 ${x | 1 < x < 5}$ D、 ${x | \frac{1}{2} \leq x < 5}$

查看试题解析
2. i为虚数单位，若 $\frac{3 + b i}{1 + i}$ 是实数，则实数b的值为（）

A、3 B、 $\frac{3}{2}$ C、 $- \frac{3}{2}$ D、-3

查看试题解析
3. 某高中学校学生人数和近视情况分别如图①和图②所示.为了解该学校学生近视形成原因，在近视的学生中按年级用分层抽样的方法抽取部分学生进行问卷调查，已知抽取到的高中一年级的学生36人，则抽取到的高三学生数为（）

A、32 B、45 C、64 D、90

查看试题解析
4. 下列函数中为奇函数且在 $(0 ， + \infty)$ 单调递增的是（）

A、 $y = x^{2} - 1$ B、 $y = 3 x - x^{3}$ C、 $y = x + \sin x$ D、 $y = x + \cos x$

查看试题解析
5. 在 ${(2 \sqrt{x} - \frac{1}{x})}^{5}$ 的展开式中，x的系数为（）

A、160 B、80 C、-80 D、-160

查看试题解析
6. 执行如图所示的程序框图，输出 $S =$ （）

A、19 B、24 C、26 D、33

查看试题解析
7. 若 $α \in (0 ， \frac{π}{2})$ ， $s i n 2 α = c o s^{2} α$ ，则 $c o s 2 α$ 的值为（）

A、 $- \frac{3}{5}$ B、 $- \frac{1}{2}$ C、0 D、 $\frac{3}{5}$

查看试题解析
8. 已知 $A$ ， $F$ 分别是椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左顶点和右焦点， $P$ 是椭圆上一点，直线 $A P$ 与直线 $l ： x = \frac{a^{2}}{c}$ 相交于点 $Q$ .且 $△ A F Q$ 是顶角为120°的等腰三角形，则该椭圆的离心率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
9. 当某种药物的浓度大于100mg/L（有效水平）时才能治疗疾病，且最高浓度不能超过1000mg/L（安全水平）．从实验知道该药物浓度以每小时按现有量14%的速度衰减．若治疗时首次服用后的药物浓度约为600mg/L，当药物浓度低于有效水平时再次服用，且每次服用剂量相同，在以下给出的服用间隔时间中，最合适的一项为（）
（参考数据： $\lg 2 \approx 0.301$ ， $\lg 3 \approx 0.477$ ， $\lg 86 \approx 1.935$ ）

A、4小时 B、6小时 C、8小时 D、12小时

查看试题解析
10. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点P是线段 $B C_{1}$ 上的一个动点，有下列三个结论：
① $A_{1} P ∥$ 面 $A C D_{1}$ ；② $B_{1} D ⊥ A_{1} P$ ；③面 $A_{1} P B ⊥$ 面 $B_{1} C D$ ．

其中所有正确结论的序号是（）

A、①②③ B、②③ C、①③ D、①②

查看试题解析
11. 已知F是抛物线C： $y^{2} = 2 p x (p > 0)$ 的焦点，过点F的直线l与抛物线交于P，Q两点，直线l与抛物线的准线 $l_{1}$ 交于点M，若 $\vec{P M} = 2 \vec{F P}$ ，则 $\frac{| F Q |}{| P Q |} =$ （）

A、 $\frac{1}{3}$ B、 $\frac{3}{4}$ C、 $\frac{4}{3}$ D、3

查看试题解析
12. 已知函数 $f (x) = {\begin{array}{l} \frac{x}{e \ln x} ， x > 1 \\ x^{3} - 3 x + 4 ， x \leq 1 \end{array}$ ，若函数 $y = {[f (x)]}^{2} + 1$ 与 $y = (4 a - 2) f (x)$ 的图象恰有5个不同公共点，则实数a的取值范围是（）

A、 $[\frac{9}{8} ， \frac{49}{24})$ B、 $(1 ， \frac{49}{24})$ C、 $(1 ， \frac{9}{8}]$ D、 $[\frac{9}{8} ， + \infty)$

查看试题解析

二、填空题

13. 已知实数 $x$ ， $y$ 满足约束条件 ${\begin{array}{l} x - y - 2 \leq 0 ， \\ 2 x + y \leq 0 ， \\ x + 1 \geq 0 ， \end{array}$ 则 $z = 2 x - y$ 的最小值为.

查看试题解析
14. 早在公元前1100年，我国数学家商高就已经知道“勾三股四弦五”，如图，在△ABC中， $B C = 3$ ， $A C = 4$ ， $A B = 5$ ，点D是CB延长线上任意一点，则 $\vec{A C} \cdot \vec{A D}$ 的值为．

查看试题解析
15. 定义运算“★”： $a ★ b = \sin a \cdot \sin b$ ．设函数 $f (x) = [(2 x) ★ (\frac{π}{6})] + [(2 x + \frac{π}{2}) ★ (\frac{π}{3})]$ ，给出下列四个结论：① $π$ 是 $f (x)$ 的最小正周期；② $f (x)$ 在 $[0 ， π]$ 有2个零点；③ $f (x)$ 在 $[0 ， \frac{π}{6}]$ 上是单调递增函数；④ $f (x)$ 的图象可以由 $y = \sin 2 x$ 的图象向右平移 $\frac{π}{6}$ 个单位长度得到．其中所有正确结论的序号是．

查看试题解析
16. 如图，AB是 $⊙ O$ 的直径，PA垂直于 $⊙ O$ 所在的平面，C是圆周上不同于A，B的任意一点， $A B = 2 A P$ ，三棱锥P-ABC体积的最大值为 $\frac{8}{3}$ ，则当△PBC的面积最大时，线段AC的长度为．

查看试题解析

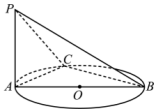
三、解答题

17. 第七次全国人口普查是对中国特色社会主义进入新时代开展的重大国情国力调查．某地区通过摸底了解到，某小区户数有1000户，在选择自主填报或人户登记的户数与户主年龄段（45岁以上和45岁及以下）分布如下2×2列联表所示：

	入户登记	自主填报	合计
户主45岁以上		200
户主45岁及以下	240		640
合计			1000

(1)、将题中列联表补充完整；通过计算判断，有没有95%的把握认为户主选择自主填报与年龄段有关系？

(2)、根据（1）中列联表的数据，在自主填报的户数中按照户主年龄段用分层抽样的方法抽取了6户．若从这6户中随机抽取3户进行进一步复核，记所抽取的3户中“户主45岁及以下”的户数为

ξ

，求

ξ

的分布列和数学期望．

附表及公式：

$P (K^{2} \geq k_{0})$	0.15	0.10	0.05	0.025	0.010
$k_{0}$	2.072	2.706	3.841	5.024	6.635

其中， $n = a + b + c + d$ ．

查看试题解析

18. 如图，已知 $O A = 10$ ，点 $B$ 是以 $O$ 为圆心，5为半径的半圆上一动点.

(1)、当 $∠ A O B = 120 °$ 时，求线段 $A B$ 的值；

(2)、若 $△ A B C$ 为正三角形，求四边形 $O A C B$ 面积的最大值.

查看试题解析
19. 设 $n \in N^{*}$ ，有以下三个条件：
① $a_{n}$ 是2与 $S_{n}$ 的等差中项；② $a_{1} = 2$ ， $S_{n + 1} = a_{1} (S_{n} + 1)$ ；③ ${a_{n}}$ 为正项等比数列， $S_{2} = 6$ ， $S_{3} = 14$ ．在这三个条件中任选一个，补充在下列问题的横线上，再作答（如果选择多个条件分别作答，按第一个解答计分）．

若数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 ${a_{n} b_{n}}$ 是以1为首项，1为公差的等差数列，求数列 ${b_{n}}$ 的前n项和 $T_{n}$ ．

查看试题解析
20. 如图，四棱锥P-ABCD中，侧面 $P A D ⊥$ 底面ABCD，底面ABCD为梯形， $A B / / D C$ ，且 $A P = P D = C D =$ $2 A B = 2 \sqrt{3}$ ， $∠ A P D = ∠ A D C = 60 °$ ．作 $P H ⊥ A D$ 交AD于点H，连结AC，BD交于点F．

(1)、设G是线段PH上的点，试探究：当G在什么位置时，有 $G F / /$ 平面PAB；

(2)、求平面PAD与平面PBC所成二面角的正弦值．

查看试题解析
21. 已知函数 $f (x) = a x \ln x + x^{2}$ ．

(1)、讨论 $f (x)$ 的零点个数；

(2)、若 $0 < a \leq 1$ ，求证： $f (x) < e^{x} - \sin x + 1$ ．

查看试题解析
22. 平面直角坐标系中，曲线 $C$ 的参数方程为 ${\begin{array}{l} x = 2 \cos φ ， \\ y = \sin φ \end{array}$ （ $φ$ 为参数）.以坐标原点为极点， $x$ 轴的非负半轴为极轴建立极坐标系，射线 $l$ 的极坐标方程为 $θ = α (0 < α < \frac{π}{2})$ ，将射线 $l$ 绕极点逆时针旋转 $\frac{π}{4}$ 后得到射线 $l_{1}$ .设 $l$ 与曲线 $C$ 相交于点 $A$ ， $l_{1}$ 与曲线 $C$ 交于点 $B$ .

(1)、求曲线 $C$ 的极坐标方程；

(2)、若 $2 \sqrt{| O A |^{2} + | O B |^{2}} = \sqrt{5} | O A | \cdot | O B |$ ，求 $α$ 的值.

查看试题解析
23. 已知函数 $f (x) = | 2 x - 4 | + | x + 1 |$ .

(1)、解不等式 $f (x) \leq 7 - x$ ；

(2)、设 $f (x)$ 的最小值为 $M$ ，正实数 $a$ ， $b$ ， $c$ 满足 $a + b = M$ ，求证： $\frac{a^{2} + 1}{a} + \frac{b^{2}}{b + 1} \geq 3$ .

查看试题解析