江苏省扬州市邗江区2021-2022学年九年级上学期期末数学试卷

试卷更新日期：2022-02-24 类型：期末考试

进入出卷网下载

一、单选题

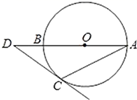
1. 下列方程中，是关于x的一元二次方程的为（）

A、 $x^{2} + \frac{1}{x^{2}} = 0$ B、x²-x-1=0 C、 $3 x^{2} - 2 x y = 0$ D、 $4 - y^{2} = 0$

查看试题解析
2. 已知 $△ A B C ∽ △ D E F$ ，且相似比为 $1 ： 2$ ，则 $△ A B C$ 与 $△ D E F$ 的周长比为（）

A、 $1 ： 4$ B、 $4 ： 1$ C、 $1 ： 2$ D、 $2 ： 1$

查看试题解析
3. 某篮球运动员在连续7场比赛中的得分（单位：分）依次为20，18，23，17，20，20，18，则这组数据的众数与中位数分别是（）

A、18分，17分 B、20分，17分 C、20分，19分 D、20分，20分

查看试题解析
4. 已知圆锥的底面半径为2cm，母线长为3cm，则其侧面积为（）cm.

A、3π B、6π C、12π D、18π

查看试题解析
5. 如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A=20°，则∠D等于（）

A、20° B、30° C、50° D、40°

查看试题解析
6. 函数y＝﹣x²﹣2x+m的图象上有两点A（1，y₁），B（2，y₂），则（）

A、y₁＜y₂ B、y₁＞y₂ C、y₁＝y₂ D、y₁、y₂的大小不确定

查看试题解析
7. 如图，在 $△$ ABC中，DE $∥$ BC，EF $∥$ AB，下列等式成立的是（）

A、 $\frac{A D}{D B} = \frac{B F}{F C}$ B、 $\frac{A D}{D B} = \frac{E C}{A E}$ C、 $\frac{A D}{D B} = \frac{D E}{B C}$ D、 $\frac{A D}{D B} = \frac{E F}{A B}$

查看试题解析
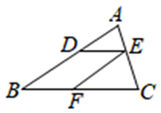8. 如图，在平面直角坐标系xOy中，已知点A（1，0），B（3，0），C为平面内的动点，且满足∠ACB=90°，D为直线y=x上的动点，则线段CD长的最小值为（）

A、1 B、2 C、 $\sqrt{2} - 1$ D、 $\sqrt{2} + 1$

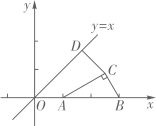查看试题解析

二、填空题

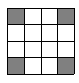
9. 一组数据6，2，–1，5的极差为.

查看试题解析
10. 若关于 $x$ 的一元二次方程 $x^{2} - 2 x + m = 0$ 有两个不相等的实数根，则实数 $m$ 的取值范围是.

查看试题解析
11. 如果在比例尺为1：1000000的地图上，A、B两地的图上距离是7.8cm，那么A、B两地的实际距离是km.

查看试题解析
12. 一只自由飞行的小鸟，如果随意落在如图所示的方格地面上（每个小方格形状完全相同），那么小鸟落在阴影方格地面上的概率是．

查看试题解析
13. 某种植基地2016年蔬菜产量为80吨，2018年蔬菜产量达到100吨，求蔬菜产量的年平均增长率，设蔬菜产量的年平均增长率为x，则可列方程为.

查看试题解析
14. 如图是二次函数y=-x²+bx+c的部分图象，若 $y \geq 0$ ，则x的取值范围是.

查看试题解析
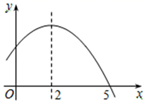15. 用半径为4，圆心角为90°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为.

查看试题解析
16. 已知抛物线y=2x²-x-1，与 $x$ 轴的一个交点为（m， 0），则代数式-4m²+2m+2022的值为.

查看试题解析
17. 如图，在△ABC中， $∠ A C B = 2 ∠ B$ ，CD平分 $∠ A C B$ .若AD＝2，BD＝3，AC的长为.

查看试题解析
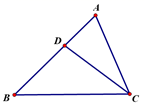18. 二次函数y＝ax²+bx+c（a，b，c是常数，a≠0）的自变量x与函数值y的部分对应值如下表：

x

…

-1

0

1

2

$\sqrt{5}$

…

y＝ax²+bx+c

…

m

-1

-1

n

t

…

当x= $- \frac{1}{2}$ 时，与其对应的函数值 $y > 0$ .有下列结论：①abc>0；②当x>1时，y随x的增大而减小；③关于x的方程ax²+bx+c＝t的两个根是 $\sqrt{5}$ 和 $1 - \sqrt{5}$ ；④ $m + n > \frac{11}{3}$ .其中，正确的结论是.

查看试题解析

三、解答题

19. 解方程：

(1)、（x+2）²﹣9＝0；

(2)、x²﹣2x﹣3＝0.

查看试题解析
20. 已知函数y＝x²-2kx＋k²+1.

(1)、求证：不论k取何值，函数y>0；

(2)、若函数图象与y轴的交点坐标为（0，10），求函数图象的顶点坐标.

查看试题解析
21. 一个不透明的口袋里装有分别标有汉字“书”、“ 香”、“ 历”、“ 城”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀．

(1)、若从中任取一个球，球上的汉字刚好是 “书”的概率为.

(2)、从中任取一球，不放回，再从中任取一球，请用树状图或列表的方法，求取出的两个球上的汉字能组成“历城”的概率．

查看试题解析
22. 已知关于x的一元二次方程kx²-4x+2=0有实数根.

(1)、求k的取值范围；

(2)、若△ABC中，AB=AC=2，AB、BC的长是方程kx²-4x+2=0的两根，求BC的长.

查看试题解析

23. 某中学九年级学生开展踢毽子活动，每班派5名学生参加，按团体总分排列名次，在规定时间内每人踢100个以上（含100）为优秀.下表是成绩最好的甲班和乙班5名学生的比赛成绩（单位：个）

	1号	2号	3号	4号	5号	总数
甲班	100	98	110	89	103	500
乙班	90	97	101	113	99	500

经统计发现两班5名学生踢毽子的总个数相等，此时有学生建议，可以通过考查数据中的其他信息为参考，请你回答下列问题：

(1)、甲班比赛数据的中位数为，乙班比赛数据的平均数为；

(2)、计算两班比赛数据的方差；

(3)、根据以上信息，你认为应该把冠军奖状发给哪一个班？简述理由.

查看试题解析

24. 如图，在矩形ABCD中，E是BC的中点，DF⊥AE，垂足为F.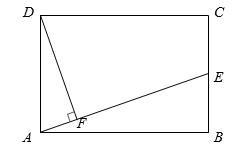

(1)、求证△ADF∽△EAB；

(2)、若AB＝12，BC＝10，求DF的长.

查看试题解析
25. 如图，在Rt $△$ ABC中，∠C＝90°，点D在AB上，以AD为直径的⊙O与BC相交于点E，与AC相交于点F，AE平分∠BAC.

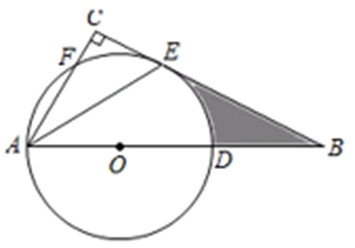(1)、求证：BC是⊙O的切线.

(2)、若∠EAB＝30°，OD＝5，求图中阴影部分的周长.

查看试题解析
26. 2022年冬奥会即将在北京召开，某网络经销商销售以冬奥会为主题的文化衫，平均每天可售出30件，每件盈利40元.为了尽快减少库存、增加盈利，该经销商采取了降价措施，经过一段时间的销售发现，销售单价每降低1元，平均每天可多售出3件.

(1)、若降价x元，则平均每天销售数量为件（用含x的代数式表示）；

(2)、若该经销商每天获得利润1800元，则每件商品应降价多少元？

(3)、若每件盈利不少于24元，不多于36元，求该经销商每天获得的最高利润和最低利润分别为多少？

查看试题解析
27. 如图1， $△$ ABC中，AC＝BC＝4，∠ACB＝90°，过点C任作一条直线CD，将线段BC沿直线CD翻折得线段CE，直线AE交直线CD于点F.直线BE交直线CD于G点.

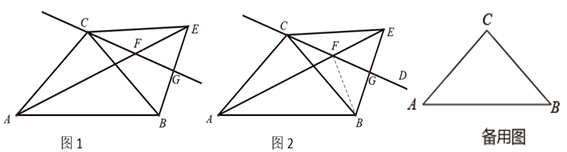(1)、小智同学通过思考推得当点E在AB上方时，∠AEB的角度是不变的，请按小智的思路帮助小智完成以下推理过程：
∵AC＝BC＝EC，

∴A、B、E三点在以C为圆心以AC为半径的圆上，

∴∠AEB＝ ∠ACB，（填写数量关系）

∴∠AEB＝ °.

(2)、如图2，连接BF，求证A、B、F、C四点共圆；

(3)、线段AE最大值为，若取BC的中点M，则线段MF的最小值为 .

查看试题解析

28. 在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程.我们对函数

y = \frac{a x}{{(x - 1)}^{2} + b}

图象与性质进行探究，下表是该函数y与自变量x的几组对应值，请解答下列问题：

…

$- 3$

$- \frac{5}{2}$

$- 2$

$- \frac{3}{2}$

$- 1$

$- \frac{1}{2}$

$\frac{1}{2}$

$1$

$\frac{3}{2}$

$2$

$\frac{5}{2}$

$3$

…

$\frac{18}{17}$

$\frac{60}{53}$

$\frac{36}{29}$

$\frac{6}{5}$

$\frac{12}{13}$

$- \frac{12}{5}$

$- 6$

$- \frac{36}{5}$

$- \frac{60}{13}$

$- \frac{18}{5}$

…

(1)、求该函数的解析式，并写出自变量x的取值范围.

(2)、表中m的值为， n的值为.

(3)、在如图所示的平面直角坐标系中，画出该函数的图象；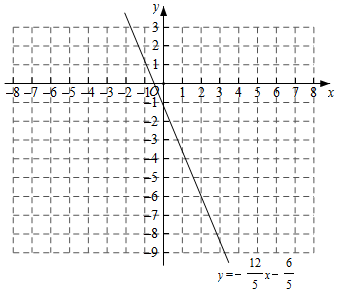

(4)、结合上述研究：①写出方程

\frac{a x}{{(x - 1)}^{2} + b} = - \frac{12}{5} x - \frac{6}{5}

的解 .

②直接写出关于x的不等式 $\frac{a x}{{(x - 1)}^{2} + b} \leq - \frac{12}{5} x - \frac{6}{5}$ 的解集是 .

查看试题解析