江苏省南京市联合体2021-2022学年九年级上学期期末数学试卷

试卷更新日期：2022-02-24 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程x²＝－2x的解是（）

A、x₁＝x₂＝0 B、x₁＝x₂＝2 C、x₁＝0，x₂＝2 D、x₁＝0，x₂＝－2

查看试题解析
2. 不透明的布袋内装有形状、大小、质地完全相同的1个白球，2个红球，3个黑球，若随机摸出一个球恰是黑球的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
3. 小明根据演讲比赛中9位评委所给的分数制作了如下表格：

平均数

中位数

众数

方差

8.0

8.2

8.3

0.2

如果去掉一个最高分和一个最低分，那么表格中数据一定不发生变化的是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
4. 如图，在△ABC中，DE∥BC， $\frac{D E}{B C}$ ＝ $\frac{1}{3}$ ，则下列结论中正确的是（）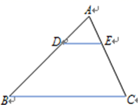

A、 $\frac{A E}{E C} = \frac{1}{3}$ B、 $\frac{A D}{A B} = \frac{1}{2}$ C、 $\frac{Δ A D E 的周长}{Δ A B C 的周长} = \frac{1}{3}$ D、 $\frac{Δ A D E 的面积}{Δ A B C 的面积} = \frac{1}{3}$

查看试题解析
5. 如图，在矩形ABCD中，E，F，G分别在AB，BC，CD上，DE⊥EF，EF⊥FG，BE＝3，BF＝2，FC＝6，则DG的长是（）

A、4 B、 $\frac{13}{3}$ C、 $\frac{14}{3}$ D、5

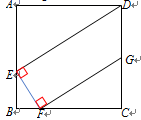查看试题解析
6. 如图，在平面直角坐标系中，将函数y＝x²－2x的图象先沿x轴翻折，再向上平移5个单位长度，得到的抛物线所对应的函数表达式是（）

A、 $y = - x^{2} + 2 x + 5$ B、 $y = - x^{2} + 2 x - 5$ C、 $y = - x^{2} - 2 x + 5$ D、 $y = - x^{2} - 2 x - 5$

查看试题解析

二、填空题

7. 若 $\frac{a}{b}$ ＝ $\frac{3}{4}$ ，则 $\frac{a + b}{b}$ ＝.

查看试题解析
8. 设x₁ ， x₂是方程x²－3x－1＝0的两个根，则x₁＋x₂＝， x₁x₂＝.

查看试题解析
9. 二次函数y＝x²－2x＋2图象的顶点坐标是.

查看试题解析
10. 已知B是线段AC的黄金分割点，AB＞BC，若AC＝6，则AB的长为.（结果保留根号）

查看试题解析
11. 如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠D＝110°，则 $\overset{⌢}{A C}$ 的长为.

查看试题解析
12. 在阳光下，身高1.6米的小明在地面上的影长为0.4米，同一时刻旗杆的影长为6米，则旗杆的高度为米.

查看试题解析
13. 如图，l₁∥l₂∥l₃ ，若AB＝2，BC＝3，AD＝1，CF＝4，则BE的长为.

查看试题解析
14. 如图，在⊙O中，AB是⊙O的内接正六边形的一边，BC是⊙O的内接正十边形的一边，则∠ABC＝°.

查看试题解析
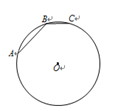15. 已知二次函数y＝ax²＋bx＋c的图象的顶点坐标为（1，m），与y轴的交点为（0，m－2），则a的值为.

查看试题解析
16. 如图，在⊙O中， $\overset{⌢}{A B}$ ＝ $\overset{⌢}{A C}$ ，AB＝10，BC＝12，D是 $\overset{⌢}{B C}$ 上一点，CD＝5，则AD的长为.

查看试题解析

三、解答题

17. 解方程：

(1)、x²－2x－3＝0；

(2)、x （x－2）－x＋2＝0.

查看试题解析
18. 从1名男生和3名女生中随机抽取参加2022年北京冬季奥运会的志愿者.

(1)、抽取2名，求恰好都是女生的概率；

(2)、抽取3名，恰好都是女生的概率是.

查看试题解析

19. 甲、乙两班各10名同学参加“国防知识”比赛，其预赛成绩如下表：

	6分	7分	8分	9分	10分
甲班	1人	2人	4人	2人	1人
乙班	2人	3人	1人	1人	3人

(1)、填写下表：

	平均数	中位数	众数
甲班	8	8
乙班			7和10

(2)、利用方差判断哪个班的成绩更加稳定？

查看试题解析

20. 如图，在Rt△ABC中，∠ACB＝90°，点D在AB上，且 $\frac{A D}{A C}$ ＝ $\frac{A C}{A B}$ .

(1)、求证 △ACD∽△ABC；

(2)、若AD＝3，BD＝2，求CD的长.

查看试题解析
21. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，F为AB延长线上一点，连接CF，DF.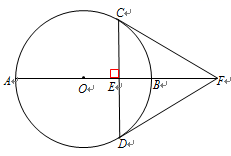

(1)、若OE＝3，BE＝2，求CD的长；

(2)、若CF与⊙O相切，求证DF与⊙O相切.

查看试题解析
22. 如图，AD和BG是△ABC的高，连接GD.

(1)、求证△ADC∽△BGC；

(2)、求证△CDG∽△CAB.

查看试题解析
23. 如图，二次函数的图象经过点（1，0），顶点坐标为（－1，－4）.

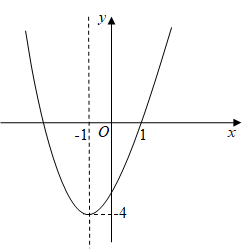(1)、求这个二次函数的表达式；

(2)、当－5＜x＜0时，y的取值范围为；

(3)、直接写出该二次函数的图象经过怎样的平移恰好过点（3，4），且与x轴只有一个公共点.

查看试题解析
24. 某超市销售一种饮料，每瓶进价为6元.当每瓶售价为10元时，日均销售量为160瓶.经市场调查表明，每瓶售价每增加0.5元，日均销售量减少10瓶.

(1)、当每瓶售价为11元时，日均销售量为瓶；

(2)、当每瓶售价为多少元时，所得日均总利润为700元？

(3)、当每瓶售价为多少元时，所得日均总利润最大？最大日均总利润为多少元？

查看试题解析
25. 如图，在⊙O中，弦AC与弦BD交于点P，AC＝BD.

(1)、求证AP＝BP；

(2)、连接AB，若AB＝8，BP＝5，DP＝3，求⊙O的半径.

查看试题解析
26. 已知函数y₁＝x＋1和y₂＝x²＋3x＋c（c为常数）.

(1)、若两个函数图象只有一个公共点，求c的值；

(2)、点A在函数y₁的图象上，点B在函数y₂的图象上，A，B两点的横坐标都为m.若A，B两点的距离为3，直接写出满足条件的m值的个数及其对应的c的取值范围.

查看试题解析
27. （数学认识）
数学是研究数量关系的一门学科，在初中几何学习的历程中，常常把角与角的数量关系转化为边与边的数量关系，把边与边的数量关系转化为角与角的数量关系.

（构造模型）

(1)、如图①，已知△ABC，在直线BC上用直尺与圆规作点D，使得∠ADB＝ $\frac{1}{2}$ ∠ACB.
（不写作法，保留作图痕迹）

(2)、如图②，若r＝5，AB＝8，求c的取值范围.

(3)、如图③，已知线段MN，AB是⊙O一条定长的弦，用直尺与圆规作点C，使得c＝MN.（不写作法，保留作图痕迹）

查看试题解析

平均数	中位数	众数	方差
8.0	8.2	8.3	0.2