江苏省连云港市海州区2021-2022学年九年级上学期期末数学试卷
试卷更新日期：2022-02-24 类型：期末考试
一、单选题
-
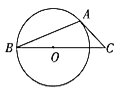
1. 在平面直角坐标系中，抛物线y=﹣（x﹣1）2+2的顶点坐标是（ ）A、（﹣1，2） B、（1，2） C、（2，﹣1） D、（2，1）2. 一个不透明的口袋里有红、黄、蓝三种颜色的小球共9个，这些球除颜色外完全相同，其中有3个黄球，2个蓝球.则随机摸出一个红球的概率为（ ）A、 B、 C、 D、3. 九年级（1）班学生在引体向上测试中，第一小组6名同学的测试成绩如下（单位：个）：4，5，6，7，7，8，这组数据的中位数与众数分别是（ ）A、7，7 B、6，7 C、6.5，7 D、5，64. 二次函数y=x2﹣x+1的图象与x轴的交点个数是（ ）A、0个 B、1个 C、2个 D、不能确定5. 如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心。若∠C=50°，则∠B的大小等于（ ）
A、20° B、25° C、40° D、50°6. 如图，在平面直角坐标中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为 ，点A，B，E在x轴上，若正方形BEFG的边长为6，则C点坐标为（ ）
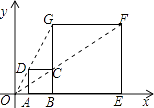A、（3，2） B、（3，1） C、（2，2） D、（4，2）7. 如图，已知△ABC与△ADE中，∠C=∠AED=90°，点E在AB上，那么添加下列一个条件后，仍无法判定△ABC∽△DAE的是（ ）
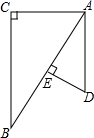A、 B、 C、 D、8. 如图所示，四边形ABCD是矩形，过点D作对角线BD的垂线，交BC的延长线于点E，取BE的中点F，连接DF，DF＝5，设AB＝x，AD＝y，则x2+（y﹣5）2的值为（ ）
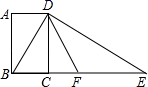A、10 B、25 C、50 D、75二、填空题
-
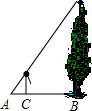
9. 函数y＝ax2（a＞0）中，当x＜0时，y随x的增大而.10. 已知 ，则 的值为 .11. 已知线段a、b、c，其中c是a、b的比例中项，若a＝2cm，b＝8cm，则线段c＝cm.12. 如图，身高为1.5米的某学生想测量一棵大树的高度，她沿着树影BA由B向A走去当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC＝3米，CA＝1米，则树的高度为米.
13. 如图，在梯形ABCD中，AD∥BC，AC与BD相交于点O，如果BC＝2AD，那么S△AOD：S△BOC的值为.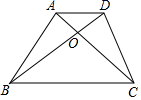
14. 如图，M是AC的中点，AB＝8，AC＝10，当AN＝时，△ABC∽△AMN.
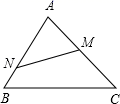15. 某一型号飞机着陆后滑行的距离y（单位：m）与滑行时间x（单位：s）之间的函数关系式是y＝﹣1.2x2+48x，该型号飞机着陆后需滑行m才能停下来.16. 如图，在矩形ABCD中，E，F分别为边AB，AD的中点，BF与EC、ED分别交于点M，N.已知AB＝4，BC＝6，则MN的长为.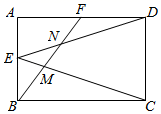
三、解答题
-
17. 解方程：x2﹣6x+8＝0．18. 如图，在矩形ABCD中，E是BC的中点，DF⊥AE，垂足为F.
(1)、求证：△ABE∽△DFA；(2)、若AB＝10，BC＝4，求DF的长.19. 已知二次函数y＝x2﹣2x﹣3
(1)、直接写出函数图象顶点坐标，并在直角坐标系中画出该二次函数的大致图象；(2)、当函数值y为正数时，自变量x的取值范围；(3)、将该函数图象向右平移一个单位，再向上平移四个单位后，所得图象的函数表达式是.20. 不透明的袋子里装有小丽刚买的红白两种色彩的手套各一双（除颜色外其余都相同）.(1)、小丽再看不见的情况下随机摸出一只手套，恰好是红色的概率是；(2)、利用画树状图或列表的方法，求小丽再看不见的情况下随机一次摸出两只手套，恰好是同色的概率.21. 如图，某公路隧道横截面为抛物线，其最大高度6米，底部宽度OM为12米，现以O点为原点，OM所在的直线为x轴建立直角坐标系.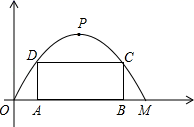
(1)、求这条抛物线的解析式；(2)、若要搭建一个由AD﹣DC﹣CB组成的矩形“支撑架”，已知支架的高度为4米，则这个“支撑架”总长是多少米？22. 如图，等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，使AE＝CF，连接AF，BE相交于点P.
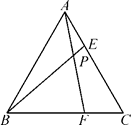(1)、求证：AF＝BE，并求∠APB的度数；(2)、若AE＝2，试求AP·AF的值.23. 因疫情防控需要，消毒用品需求量增加.某药店新进一批桶装消毒液，每桶进价50元，每天销售量y（桶）与销售单价x（元）之间满足一次函数关系，其图象如图所示.
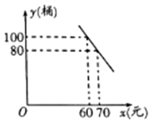(1)、求y与x之间的函数表达式；(2)、每桶消毒液的销售价定为多少元时，药店每天获得的利润最大，最大利润是多少元？（利润=销售价-进价）24. 如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PB、AB，∠PBA＝∠C.
(1)、求证：PB是⊙O的切线；(2)、连接OP，若OP∥BC，且OP＝8，⊙O的半径为3，求BC的长.25. 如图，△ABC中，∠C＝90°，AC＝3，BC＝4，在线段AB上，动点M从点A出发向点B做匀速运动，同时动点N从B出发向点A做匀速运动，当点M、N其中一点停止运动时，另一点也停止运动，分别过点M、N作AB的垂线，分别交两直角边AC，BC所在的直线于点D、E，连接DE，若运动时间为t秒，在运动过程中四边形DENM总为矩形（点M、N重合除外）.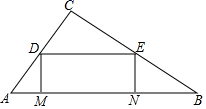
(1)、写出图中与△ABC相似的三角形；(2)、如图，设DM的长为x，矩形DENM面积为S，求S与x之间的函数关系式；当x为何值时，矩形DENM面积最大？最大面积是多少？(3)、在运动过程中，若点M的运动速度为每秒1个单位长度，求点N的运动速度.求t为多少秒时，矩形DEMN为正方形？26. 如图所示，抛物线y＝ax2+bx﹣3与x轴相交于A（-1，0）、B（3，0）两点，与y轴相交于点C，点M为抛物线的顶点.
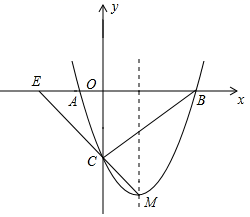(1)、求抛物线的函数关系式.(2)、若点D是抛物线对称轴上的动点，点G是抛物线上的动点，是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在，求出点G的坐标；若不存在，试说明理由.(3)、直线CM交x轴于点E，若点P是线段EM上的一个动点，是否存在以点P、E、O为顶点的三角形与△ABC相似.若存在，求出点P的坐标；若不存在，请说明理由.