2021-2022学年浙教版数学七下3.4 乘法公式同步练习

试卷更新日期：2022-02-24 类型：同步测试

进入出卷网下载

一、单选题

1. 计算下列各式，其结果为a²-1的是（）

A、（a-1）² B、（-a-1）（a+1） C、（-a+1）（-a+1） D、（-a+1）（-a-1）

查看试题解析
2. 计算（x-y）（-y-x）的结果是（）

A、-x²+y² B、-x²-y² C、x^2-y² D、x²+y²

查看试题解析
3. 已知x，y满足方程组 ${\begin{cases} x + 2 y = - 1 \\ x - 2 y = 5 \end{cases}$ ，则x^2-4y²的值为（）

A、-5 B、4 C、5 D、25

查看试题解析
4. 下列各式中，不能运用平方差公式进行运算的是（）

A、（3x+7y）（3x-7y） B、（5m-n）（n-5m） C、（-0.2x-0.3）（-0.2x+0.3） D、（-3n-mn）（3n-mn）

查看试题解析
5. 下列运算正确的是（）

A、(x+y)² =x²+y² B、(x-y)²=x²+2xy+y² C、(x+y)² =x²+y² +2xy D、(x-y)²=x²-xy+y²

查看试题解析
6. 在下列各式中，一定能用平方差公式因式分解的是（）．

A、 $- a^{2} - 9$ B、 $a^{2} - 9$ C、 $a^{2} - 4 b$ D、 $a^{2} + 9$

查看试题解析
7. 已知两个不等于0的实数 $a$ 、 $b$ 满足 $a + b = 0$ ，则 $\frac{b}{a} + \frac{a}{b}$ 等于（）

A、-2 B、-1 C、1 D、2

查看试题解析
8. 如果x+y＝6，x²-y²=24，那么y-x的值为（）

A、﹣4 B、4 C、﹣6 D、6

查看试题解析
9. 若 $(2 a + 3 b) () = 9 b^{2} - 4 a^{2}$ ，则括号内应填的代数式是（）．

A、 $- 2 a - 3 b$ B、 $2 a + 3 b$ C、 $2 a - 3 b$ D、 $3 b - 2 a$

查看试题解析
10. 下列各式中：① $x^{2} - 2 x y + y^{2}$ ；② $\frac{1}{2} a^{2} + a b + \frac{1}{2} b^{2}$ ；③ $- 4 a b - a^{2} + 4 b^{2}$ ；④ $4 x^{2} + 9 y^{2} - 12 x y$ ；⑤ $3 x^{2} - 6 x y + 3 y^{2}$ ．能用完全平方公式分解的个数有（）

A、5个 B、4 个 C、3 个 D、2个

查看试题解析

二、填空题

11. $(a + 2) (a - 2) =$ ．

查看试题解析
12. 若x²-2xy+y²=4，则x-y的值为.

查看试题解析
13. 计算 ${(a - 3)}^{2}$ 的结果为

查看试题解析
14. 已知a﹣b＝7，ab＝2，则（a+b）²＝．

查看试题解析
15. 计算（2a + 3b）²=.

查看试题解析
16. 计算（a－b）²－（a＋b）²的结果是.

查看试题解析

三、解答题

17. 已知a，b，c是 $△ A B C$ 的三边长，且满足 $a^{2} + b^{2} - 4 a - 8 b + 20$ ＝ $0$ ， $c$ ＝ $3 c m$ ，求 $△ A B C$ 的周长．

查看试题解析
18. 先化简，再求值： $(2 + x) (2 - x) + (x - 1) (x + 5)$ ，其中 $x = \frac{3}{2}$ ．

查看试题解析
19. 先化简，再求值：（2x+1）（2x﹣1）﹣3x（x+1）﹣（x﹣1）² ，当x=﹣1．

查看试题解析
20. 数学课上老师出一道题，用简便方法计算 $296^{2}$ 的值，喜欢数学的小亮举手做出了这道题，他的解题过程如下：
$296^{2} = {(300 - 4)}^{2}$ 第一步

$= 300^{2} - 2 \times 300 \times (- 4) + 4^{2}$ 第二步

$= 90000+2400+16$ 第三步

$= 92416$ 第四步

老师表扬小亮积极发言的同时，也指出了解题中的不正确.

(1)、你认为小亮的解题过程中，从第步开始出错.

(2)、请你写出正确的解题过程.

查看试题解析
21. 乘法公式的探究及应用：

(1)、如图，可以求出阴影部分的面积是（写成两数平方差的形式）；

(2)、如图，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是，长是，面积是（写成多项式乘法的形式）；

(3)、比较左、右两图的阴影部分面积，可以得到乘法公式：（用式子表达）；

(4)、运用你所得到的公式，计算下列式子：（2m+n﹣p）（2m﹣n+p）

查看试题解析
22. 图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．

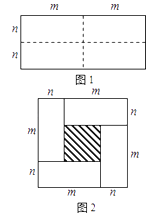
(1)、请写出图2中阴影部分的面积；

(2)、观察图2你能写出下列三个代数式之间的等量关系吗？
代数式：（m+n）² ，（m﹣n）² ， mn；

(3)、根据（2）中的等量关系，解决如下问题：若a+b=7，ab=5，求（a﹣b）²的值．

查看试题解析
23. 已知代数式6x²+bx﹣y+5﹣2ax²+x+5y﹣1的值与字母x的取值无关

(1)、求a、b的值；

(2)、求a²﹣2ab+b²的值．

查看试题解析
24. 探索代数式a²﹣b²与代数式（a+b）（a﹣b）的关系.

(1)、当a=5，b=2时,分别计算两个代数式的值．

(2)、当a=7，b=﹣13时,分别计算两个代数式的值．

(3)、你发现了什么规律?

(4)、利用你发现的规律计算：889²﹣111² ．

查看试题解析