2021-2022学年浙教版数学七下第二章二元一次方程组单元检测卷

试卷更新日期：2022-02-23 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列方程：①x+y=1；②2x- $\frac{y}{2}$ =1；③x²+y²=1；④5（x+y）=7（x-y）；⑤x²=1；⑥x+ $\frac{1}{2}$ =4，其中是二元一次方程的是（）

A、① B、①③ C、①②④ D、①②④⑥

查看试题解析
2. 二元一次方程3x+2y=18的正整数解有（）

A、1组 B、2组 C、3组 D、4组

查看试题解析
3. 解方程组 ${\begin{cases} 3 x - y + 2 z = 3 \\ 2 x + y - 4 z = 11 \\ 7 x + y - 5 z = 1 \end{cases}$ ，若要使运算简便，消元的方法应选取（）

A、先消去x B、先消去y C、先消去z D、以上说法都不对

查看试题解析
4. 已知方程2x^m+1+3y²ⁿ=5是二元一次方程，则m，n的值分别为（）

A、-1，0 B、0，1 C、0， $\frac{1}{2}$ D、-1， $\frac{1}{2}$

查看试题解析
5. 已知x=2，y=﹣1是方程ax+y=3的一组解，则a的值为（）

A、2 B、1 C、﹣1 D、﹣2

查看试题解析
6. 若方程组 ${\begin{array}{l} 5 x - 3 y = 7 \\ 7 x - 5 y = 3 \end{array}$ 的解为 ${\begin{array}{l} x = 6.5 \\ y = 8.5 \end{array}$ ，则方程组 ${\begin{array}{l} 5 (x - 13) - 3 (y + 1) = 7 \\ 7 (x - 13) - 5 (y + 1) = 3 \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 19.5 \\ y = 9.5 \end{array}$ B、 ${\begin{array}{l} x = 19.5 \\ y = 7.5 \end{array}$ C、 ${\begin{array}{l} x = - 6.5 \\ y = 9.5 \end{array}$ D、 ${\begin{array}{l} x = - 6.5 \\ y = 7.5 \end{array}$

查看试题解析
7. 二元一次方程组 ${\begin{array}{l} 3 x + 2 y = 13 \\ 8 x - 2 y = 20 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 5 \\ y = - 1 \end{array}$ B、 ${\begin{array}{l} x = 4 \\ y = \frac{1}{2} \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = - 2 \end{array}$

查看试题解析
8. 佳佳坐在匀速行驶的车上，将每隔一段时间看到的里程碑上的数描述如下：
时刻
12：00
13：00
14：00
里程碑上的数
是一个两位数，数字之和为7
十位数字和个位数字与12：00时看到的刚好相反
比12：00看到的两位数中间多了个0
则12：00时看到的两位数是（）

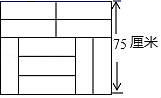
A、16 B、25 C、34 D、52

查看试题解析
9. 如图，8块相同的小长方形地砖拼成一个大长方形，设每块小长方形地砖的长为x cm，宽为y cm，下列方程组正确的是（）

A、 ${\begin{array}{l} 2 x = 80 \\ x = 2 y \end{array}$ B、 ${\begin{array}{l} 2 x = 80 \\ 2 x = x + 3 y \end{array}$ C、 ${\begin{array}{l} x + y = 80 \\ 2 x = x + 3 y \end{array}$ D、 ${\begin{array}{l} x + y = 80 \\ x = 2 y \end{array}$

查看试题解析
10. 为确保信息安全，信息需要加密传输，发送方由明文→密文（加密），接收方由密文→明文（解密），已知加密规则为：明文a，b，c对应密文a+1，-a+2b+4，b+3c+9，如果接收方收到密文7，12，22，则解密得到的明文为（）

A、6，2，7 B、2，6，7 C、6，7，2 D、7，2，6

查看试题解析

二、填空题

11. 已知二元一次方程 $\frac{x}{4}$ + $\frac{y}{2}$ =1，用含x的代数式表示y，则y= ，用含y的代数式表示x，则x=.

查看试题解析
12. 实数x，y，z满足2x+y-3z=5，x+2y+z=-4，请用含x的代数式表示z，即.

查看试题解析
13. 为了保护环境，某校环保小组成员小明收集废电池，第一天收集1号电池4节，5号电池5节，总质量为460克；第二天收集1号电池2节，5号电池3节，总质量为240克，则1号电池每节重为克，5号电池每节重为克.

查看试题解析
14. 若关于x、y 的二元一次方程组 ${\begin{array}{l} x - y = 2 m + 1 \\ x + 3 y = 3 \end{array}$ 的解满足x+y=1，则m的值为．

查看试题解析
15. 关于x，y的二元一次方程组 ${\begin{cases} 2 x + 3 y = m \\ x + y = 2 \end{cases}$ 的解是正整数，则整数m的值为正整数，则整数m的值为.

查看试题解析
16. 动物园有一群鸵鸟和长颈鹿，它们共有30只眼睛和44只脚，则鸵鸟有只，长颈鹿有只.

查看试题解析

三、解答题

17. 已知关于x，y的方程（m²-4）x²+（m+2）x+3y=5

(1)、当m取何值时，这个方程是一元一次方程？

(2)、当m取何值时，这个方程是二元一次方程？

查看试题解析
18. 阅读下列材料，解答下面的问题：我们知道方程 $2 x + 3 y = 12$ 有无数个解，但在实际问题中往往只需求出其正整数解.例：由 $2 x + 3 y = 12$ ，得： $y = \frac{12 - 2 x}{3} = 4 - \frac{2}{3} x$ （ $x$ 、 $y$ 为正整数）.要使 $y = 4 - \frac{2}{3} x$ 为正整数，则 $\frac{2}{3} x$ 为正整数，可知： $x$ 为3的倍数，从而 $x = 3$ ，代入 $y = 4 - \frac{2}{3} x = 2$ .所以 $2 x + 3 y = 12$ 的正整数解为 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ .问题：

(1)、请你直接写出方程 $3 x + 2 y = 8$ 的正整数解.

(2)、若 $\frac{6}{x - 3}$ 为自然数，则求出满足条件的正整数 $x$ 的值.

(3)、关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} x + 2 y = 9 \\ 2 x + k y = 10 \end{array}$ 的解是正整数，求整数 $k$ 的值.

查看试题解析
19. 某厂用如图甲所示的长方形和正方形纸板做成如图乙所示的A，B，两种长方体形状的无盖纸盒.现有正方形纸板140张，长方形纸板360张，刚好全部用完，问能做成多少个A型盒子？多少个B型盒子？

(1)、根据题意，甲和乙两同学分别列出的方程组如下：甲： ${\begin{matrix} x + 2 y = 140 \\ 4 x + 3 y = 360 \end{matrix}$ ，
乙： ${\begin{matrix} x + y = 140 \\ 4 x + \frac{3}{2} y = 360 \end{matrix}$ ，根据两位同学所列的方程组，请你分别指出未知数 $x ， y$ 表示的意义：甲： $x$ 表示， $y$ 表示；乙： $x$ 表示， $y$ 表示.

(2)、求出做成的A型盒子和B型盒子分别有多少个?

查看试题解析
20. 在等式y=ax²+bx+c中，当x=-1时，y=4；当x=2时，y=4；当x=1时，y=2.

(1)、求a，b，c的值；

(2)、当x=-2时，求y的值.

查看试题解析
21.

(1)、 $\frac{x + 1}{2} = x - 1$

(2)、 ${\begin{array}{l} \frac{x}{2} - \frac{y + 1}{3} = 1 \\ 3 x + 2 y = 4 \end{array}$

查看试题解析
22. 某同学在解关于x，y的方程组 ${\begin{array}{l} a x + b y = 2 \\ c x - 7 y = 8 \end{array}$ 时，本应解出 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ ，由于看错了系数c，而得到 ${\begin{array}{l} x = - 2 \\ y = 2 \end{array}$ ，求 $a + b - c$ 的值.

查看试题解析
23. 如图，用 10 块相同的小长方形地砖拼成一个宽是 75 厘米的大长方形，用列方程或方程组的方法，求每块小长方形地砖的长和宽分别是多少厘米？

查看试题解析
24. 阅读理解.
小聪在解方程组 ${\begin{cases} 2 x + 5 y = 3 ① \\ 4 x + 11 y = 5 ② \end{cases}$ 时，发现方程组中①和②之间存在一定的关系，他发现了一种“整体代换”法，具体解法如下：

解：将方程②变形为4x+10y+y=5，

即2（2x+5y）+y=5，③

把方程①代入方程③，得2×3+y=5，解得y=-1把y=-1

代入方程①，得x=4

∴方程组的解是 ${\begin{cases} x = 4 \\ y = - 1 \end{cases}$

(1)、仿照小聪的解法，解方程组 ${\begin{cases} 3 x - 2 y = 5 ① \\ 9 x - 4 y = 19 ② \end{cases}$

(2)、已知x，y满足方程组 ${\begin{cases} 3 x^{2} - 2 x y + 12 y^{2} = 47 ① \\ 2 x^{2} + x y + 8 y^{2} = 36 ② \end{cases}$
（i）求x²+4y²的值；

（ⅱ）求3xy的值.

查看试题解析

时刻	12：00	13：00	14：00
里程碑上的数	是一个两位数，数字之和为7	十位数字和个位数字与12：00时看到的刚好相反	比12：00看到的两位数中间多了个0

2021-2022学年浙教版数学七下第二章二元一次方程组 单元检测卷

一、单选题

二、填空题

三、解答题

2021-2022学年浙教版数学七下第二章二元一次方程组单元检测卷