人教版数学八年级下册第十七章勾股定理
试卷更新日期:2022-02-23 类型:同步测试
一、单选题
-
1. 在平面直角坐标系中,点 到原点的距离是( )A、 B、 C、 D、2. 在直角三角形中,若两边长分别为3和4,则第三边的平方为( )A、25或7 B、25 C、7 D、53. 我国汉代的赵爽在注释《周髀算经》时给出了勾股定理的无字证明,人们称它为“赵爽弦图”,“赵爽弦图”指的是( )A、
 B、
B、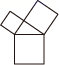 C、
C、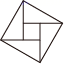 D、
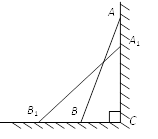
D、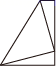 4. 已知一个直角三角形的两直角边长分别为5和12,则第三边长是( )A、13 B、14 C、15 D、165. 下列四组数据为三角形的三边,其中能构成直角三角形的是( )A、 ; B、 ; C、 ; D、 .6. 如图,在△ 中,∠ ,∠ , ;以点 为圆心, 为半径画弧交 于点 ,再以点 为圆心, 为半径画弧交 于点 ,则 的长等于( )
4. 已知一个直角三角形的两直角边长分别为5和12,则第三边长是( )A、13 B、14 C、15 D、165. 下列四组数据为三角形的三边,其中能构成直角三角形的是( )A、 ; B、 ; C、 ; D、 .6. 如图,在△ 中,∠ ,∠ , ;以点 为圆心, 为半径画弧交 于点 ,再以点 为圆心, 为半径画弧交 于点 ,则 的长等于( ) A、 B、 C、 D、17. 我国古代数学著作《九章算术》记载了一道有趣的问题,原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设水深为x尺,根据题意,可列方程为( )
A、 B、 C、 D、17. 我国古代数学著作《九章算术》记载了一道有趣的问题,原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设水深为x尺,根据题意,可列方程为( ) A、 B、 C、 D、8. △ABC中∠A、∠B、∠C的对边分别是a、b、c,下列命题为真命题的( )A、如果∠A=2∠B=3∠C,则△ABC是直角三角形 B、如果∠A:∠B:∠C=3:4:5,则△ABC是直角三角形 C、如果a:b:c=1:2:2,则△ABC是直角三角形 D、如果a:b;c=3:4: ,则△ABC是直角三角形9. 如图,分别以直角三角形各边为一边向三角形外部作正方形,其中两个小正方形的面积分别为9和25,则正方形A的面积是( )
A、 B、 C、 D、8. △ABC中∠A、∠B、∠C的对边分别是a、b、c,下列命题为真命题的( )A、如果∠A=2∠B=3∠C,则△ABC是直角三角形 B、如果∠A:∠B:∠C=3:4:5,则△ABC是直角三角形 C、如果a:b:c=1:2:2,则△ABC是直角三角形 D、如果a:b;c=3:4: ,则△ABC是直角三角形9. 如图,分别以直角三角形各边为一边向三角形外部作正方形,其中两个小正方形的面积分别为9和25,则正方形A的面积是( ) A、16 B、32 C、34 D、6410. 1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边 , 在一条直线上,证明中用到的面积相等关系是( )
A、16 B、32 C、34 D、6410. 1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边 , 在一条直线上,证明中用到的面积相等关系是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
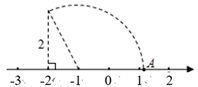
11. 如图,在数轴上点A表示的实数是 .
 12. 一木杆在离地面3米处折断,木杆顶端落在离木杆底端4米处,木杆折断之前高米.13. 图中阴影部分是一个正方形,则此正方形的面积为cm2.
12. 一木杆在离地面3米处折断,木杆顶端落在离木杆底端4米处,木杆折断之前高米.13. 图中阴影部分是一个正方形,则此正方形的面积为cm2. 14. 直角三角形的直角边长分别为 , ,斜边长为 ,则 .15. 生活经验表明:靠墙摆放梯子时,若梯子底端离墙约为梯子长度的 时,则梯子比较稳定.现有一长度为9 m的梯子,当梯子稳定摆放时,它的顶端能到达8.5 m高的墙头吗?(填“能”或“不能”).16. 如图,一棵大树在一次强台风中于离地面 处折断倒下,树干顶部在距离根部 处,这棵大树在折断前的高度为 .
14. 直角三角形的直角边长分别为 , ,斜边长为 ,则 .15. 生活经验表明:靠墙摆放梯子时,若梯子底端离墙约为梯子长度的 时,则梯子比较稳定.现有一长度为9 m的梯子,当梯子稳定摆放时,它的顶端能到达8.5 m高的墙头吗?(填“能”或“不能”).16. 如图,一棵大树在一次强台风中于离地面 处折断倒下,树干顶部在距离根部 处,这棵大树在折断前的高度为 .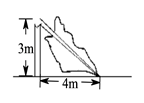
三、解答题
-
17. 如图,每个小正方形的边长是1
 (1)、在图①中画出一个面积为2的直角三角形;
(1)、在图①中画出一个面积为2的直角三角形;
(2)、在图②中画出一个面积是2的正方形.18. 一个零件的形状如图所示,已知AC=3 ,AB=4 ,BD=12 求CD的长.