陕西省宝鸡市2022届高三上学期理数高考模拟检测试卷（一）

试卷更新日期：2022-02-23 类型：高考模拟

进入出卷网下载

一、单选题

1. 集合 $M = {x | x^{2} - x - 2 = 0}$ ， $N = {- 2 ， - 1 ， 0 ， 1 ， 2}$ ，则 $M ∩ N =$ （）

A、 ${- 1 ， 2}$ B、 ${- 2 ， 1}$ C、{-2} D、{2}

查看试题解析
2. 复数 $z = \frac{2}{1 + i}$ 的模为（）

A、1 B、2 C、 $\sqrt{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
3. 某乡镇实现脱贫目标后，在奔小康的道路上，继续大步前进，依托本地区苹果种植的优势，经过3年的发展，苹果总产量翻了一番，统计苹果的品质得到了如下饼图：70，80是指苹果的外径，则以下说法中不正确的是（）

A、80以上优质苹果所占比例增加 B、经过3年的努力，80以上优质苹果产量实现翻了一番的目标 C、70~80的苹果产量翻了一番 D、70以下次品苹果产量减少了一半

查看试题解析
4. 下边程序框图的算法思想源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“ $m$ MOD $n$ ”表示 $m$ 除以 $n$ 的余数），若输入的 $m$ ， $n$ 分别为297，57，则输出的 $m =$ （）

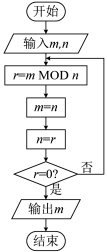A、3 B、6 C、9 D、12

查看试题解析
5. 已知函数 $f (x) = {\begin{array}{l} x + 2 ， (x \leq 0) ， \\ x + \frac{1}{x} ， (x > 0) ， \end{array}$ 则 $f (f (a)) = 2$ ，则 $a =$ （）

A、0或1 B、-1或1 C、0或-2 D、-2或-1

查看试题解析
6. 某机构通过抽样调查，利用 $2 \times 2$ 列联表和 $K^{2}$ 统计量研究患肺病是否与吸烟有关，计算得 $K^{2} = 3.305$ ，经查对临界值表知 $P (K^{2} \geq 2.706) \approx 0.10$ ， $P (K^{2} \geq 3.841) \approx 0.05$ ，现给出四个结论，其中正确的是（）

A、因为 $K^{2} ＞ 2.706$ ，故有90%的把握认为“患肺病与吸烟有关" B、因为 $K^{2} < 3.841$ ，故有95%的把握认为“患肺病与吸烟有关” C、因为 $K^{2} ＞ 2.706$ ，故有90%的把握认为“患肺病与吸烟无关” D、因为 $K^{2} < 3.841$ ，故有95%的把握认为“患肺病与吸烟无关”

查看试题解析
7. 函数 $f (x) = s i n x - c o s x$ 的图像可以由函数 $g (x) = s i n x + c o s x$ 的图像（）

A、向右平移 $\frac{π}{4}$ 单位得到 B、向左平移 $\frac{π}{4}$ 单位得到 C、向右平移 $\frac{π}{2}$ 单位得到 D、向左平移 $\frac{π}{2}$ 单位得到

查看试题解析
8. $α$ ， $β$ 是两个不同的平面， $m$ ， $n$ 是两条不同的直线，则下列命题中真命题的个数为（）
①若 $m ∥ n$ ， $α ∥ β$ ，则 $m$ 与 $α$ 所成的角等于 $n$ 与 $β$ 所成的角；②若 $m \subset$ $α$ ， $n ∩ α = A$ ， $A \notin m$ ，则 $m$ 与 $n$ 是异面直线；③若 $m$ $\subset α$ ， $n \subset$ $β$ ， $α ∥ β$ ，则 $m ∥ n$ ；④若 $α ⊥ β$ ， $α ∩ β = m$ ， $n ⊥ m$ ，则 $n ⊥ α$

A、1 B、2 C、3 D、4

查看试题解析
9. 已知 $F_{1}$ ､ $F_{2}$ 是双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左､右焦点，过 $F_{1}$ 的直线 $l$ 与双曲线的左支交于点 $A$ ，与右支交于点 $B$ ，若 $| A F_{1} | = 2 a$ ，且 $| A B | = | A F_{2} |$ ，则双曲线的离心率为（）

A、 $\frac{\sqrt{7}}{2}$ B、 $\sqrt{7}$ C、 $\sqrt{5}$ D、 $\frac{5}{3}$

查看试题解析
10. 已知抛物线 $C ： y^{2} = 16 x$ ，直线 $l ： x = 4$ 与 $C$ 交于 $A$ ， $B$ 两点， $M$ 是射线 $B A$ 上异于 $A$ ， $B$ 的动点，圆 $C_{1}$ 与圆 $C_{2}$ 分别是 $△ O M A$ 和 $△ O M B$ 的外接圆（ $O$ 为坐标原点），则圆 $C_{1}$ 与圆 $C_{2}$ 面积的比值（）

A、小于1 B、大于1 C、等于1 D、与 $M$ 点的位置有关

查看试题解析
11. 已知定点 $A (0 ， 1)$ ， $P$ 是圆 $C ： {(x - 2)}^{2} + {(y - m)}^{2} = 1 (m \in R)$ 上的动点，则“ $m = 1$ ”是“ $∠ P A C$ 的最大值为30°”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
12. 已知 $a > 1$ ， $b > 1$ ，则下列关系式不可能成立的是（）

A、 $e^{b} l n a \leq a b$ B、 $e^{b} l n a \geq a b$ C、 $a e^{b} \geq b l n a$ D、 $a e^{b} \leq b l n a$

查看试题解析

二、填空题

13. 已知平面向量 $\vec{a} = (- 1 ， m)$ ， $\vec{b} = (2 ， 3 - m)$ ，若 $\vec{a} ∥ \vec{b}$ ，则 $m =$ .

查看试题解析
14. ${(1 - x)}^{2} {(1 + x)}^{4}$ 展开式中 $x^{2}$ 的系数为.

查看试题解析
15. 已知 $α$ ､ $β$ 均为锐角，且 $c o s (α + β) = \frac{1}{7}$ ， $s i n (β - \frac{π}{6}) = \frac{1}{2}$ ，则 $c o s α =$ .

查看试题解析
16. 已知正三棱锥 $S - A B C$ 的底面边长为 $3 \sqrt{2}$ ， $P$ ， $Q$ ， $R$ 分别是棱 $S A$ ， $A B$ ， $A C$ 的中点，若 $△ P Q R$ 是等腰直角三角形，则该三棱锥的外接球的表面积为．

查看试题解析

三、解答题

17. 已知 ${a_{n}}$ 是等差数列， $a_{1} + a_{2} + a_{3} = 12$ ， $a_{4} = 8$ .

(1)、求 ${a_{n}}$ 的通项公式；

(2)、若对于任意 $n \in N_{+}$ ，点 $A_{n} (a_{n} ， b_{n})$ 都在曲线 $y = 2^{x}$ 上，过 $A_{n}$ 作 $x$ 轴的垂线，垂足为 $B_{n}$ ，记 $△ O A_{n} B_{n}$ 的面积为 $S_{n}$ ，求数列 ${S_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
18. 如图，四棱锥 $P - A B C D$ 的底面为正方形， $P A ⊥$ 平面 $A B C D$ ， $M$ 是 $P C$ 的中点， $P A = A B$ .

(1)、求证： $A M ⊥$ 平面 $P B D$ ；

(2)、求二面角 $P - B D - M$ 的余弦值.

查看试题解析
19. “ $X$ 病毒”给人类社会带来了极大的危害，我国政府和人民认识到对抗“ $X$ 病毒”是一项长期而艰巨的任务，为了加强后备力量的培养，某地政府组织卫生､学校等部门，开展了一次“ $X$ 病毒”检测练兵活动.活动组织者把3份不同的“X病毒”咽拭子随机分到3个组，并根据份额，增加不含“ $X$ 病毒”的正常咽拭子，使每组有20份咽拭子.规定每组先混合检测，即将20份咽拭子分别取样混合在一起检验，若结果为阴性，则这20份咽拭子全为阴性，只需检验一次就够了；若检验结果为阳性，为了明确这20份咽拭子究竟哪份为阳性，就需要对这20份再逐一检验，此时这20份咽拭子的检验次数总共为21次.三组样本检验规则相同，每次检测费为60元.

(1)、求检测次数为23次的概率；

(2)、设本次活动检测总费用为 $Y$ 元，求 $Y$ 的分布列及数学期望.

查看试题解析
20. 椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 经过点 $P (1 ， \frac{\sqrt{2}}{2})$ ，且两焦点与短轴的两个端点的连线构成一个正方形.

(1)、求椭圆 $C$ 的方程；

(2)、设 $M (\frac{5}{4} ， 0)$ ，过椭圆 $C$ 的右焦点 $F$ 作直线 $l$ 交 $C$ 于 $A$ 、 $B$ 两点，试问： $\vec{M A} \cdot \vec{M B}$ 是否为定值？若是，求出这个定值；若不是，请说明理由.

查看试题解析
21. 已知函数 $f (x) = (x - a) l n x + x^{2}$

(1)、当 $a = 2$ 时，求函数 $f (x)$ 在区间 $[1 ， e]$ 上最大值和最小值；

(2)、令 $g (x) = f (x) - x^{2} + x$ ，当函数 $g (x)$ 恰有两个极值点时，求实数 $a$ 的取值范围.

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，直线 $l$ 的参数方程为 ${\begin{array}{l} x = t \\ y = k t \end{array}$ （ $t$ 为参数），曲线 $C$ 的参数方程为 ${\begin{array}{l} x = 2 + c o s φ \\ y = s i n φ \end{array}$ （ $ϕ$ 为参数），以坐标原点为极点， $x$ 轴的非负半轴为极轴建立极坐标系．

(1)、求直线 $l$ 的普通方程和曲线 $C$ 的极坐标方程；

(2)、若直线 $l$ 和曲线 $C$ 交于 $A$ ， $B$ 两点，且 $\vec{O A} = 3 \vec{A B}$ ，求实数 $k$ 的值．

查看试题解析
23. 关于 $x$ 的不等式 $| a x - 3 | \leq x$ 的解集为 $[1 ， b]$ ，其中 $a > 1$ ．

(1)、求实数 $a$ ， $b$ 的值；

(2)、若正数 $m$ ， $n$ 满足 $m + \frac{2}{n} = a$ ，求 $\frac{2}{m} + n$ 的最小值．

查看试题解析