山西省吕梁市2022届高三上学期理数第一次模拟考试试卷
试卷更新日期:2022-02-23 类型:高考模拟
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 若 , 则( )A、 B、 C、 D、3. 函数的零点个数为( )A、1 B、2 C、3 D、44. 如图正三棱柱的各棱长相等,为的中点,则异面直线与所成的角为( )
 A、 B、 C、 D、5. 函数的大致图象为( )A、
A、 B、 C、 D、5. 函数的大致图象为( )A、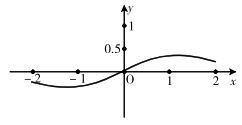 B、
B、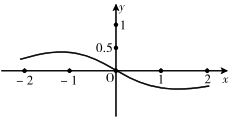 C、
C、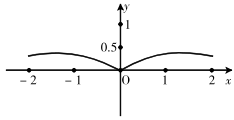 D、
D、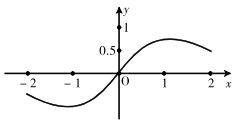 6. 如图,在正方形网格中有向量 , , , 若 , 则( )
6. 如图,在正方形网格中有向量 , , , 若 , 则( )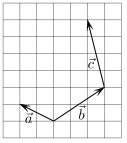 A、 , B、 , C、 D、7. “”是“函数在处有极大值”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件8. 过双曲线:的右焦点作圆的一条切线,切点为B,交y轴于D,若 , 则双曲线C的离心率为( )A、 B、 C、2 D、9. 在△中,D为BC的中点, , , EF与AD交于G, , 则( )
A、 , B、 , C、 D、7. “”是“函数在处有极大值”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件8. 过双曲线:的右焦点作圆的一条切线,切点为B,交y轴于D,若 , 则双曲线C的离心率为( )A、 B、 C、2 D、9. 在△中,D为BC的中点, , , EF与AD交于G, , 则( ) A、 B、 C、 D、10. 摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.如图,某摩天轮最高点距离地面高度为120m,转盘直径为110m,设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要30min.游客甲坐上摩天轮的座舱,开始转动tmin后距离地面的高度为Hm,如图以轴心O为原点,与地面平行的直线为x轴建立直角坐标系,在转动一周的过程中,H关于t的函数解析式为( )
A、 B、 C、 D、10. 摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.如图,某摩天轮最高点距离地面高度为120m,转盘直径为110m,设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要30min.游客甲坐上摩天轮的座舱,开始转动tmin后距离地面的高度为Hm,如图以轴心O为原点,与地面平行的直线为x轴建立直角坐标系,在转动一周的过程中,H关于t的函数解析式为( )
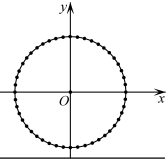 A、 , B、 , C、 , D、 ,11. 已知为数列的前n项和,且 , , 则( )A、 B、 C、 D、12. 若 , 则( )A、 B、 C、 D、
A、 , B、 , C、 , D、 ,11. 已知为数列的前n项和,且 , , 则( )A、 B、 C、 D、12. 若 , 则( )A、 B、 C、 D、二、填空题
-
13. 已知为椭圆的左焦点,P为椭圆上一点,则的取值范围为 .14. 已知函数的图象和直线有三个交点,则 .15. 已知P为圆C:上一动点,点Q的坐标为 , 若 , 则(O为坐标原点)的最小值为 .16. 公园,旅游景点的护栏顶部常常用“半正多面体”装饰.半正多面体是由两种或两种以上的正多边形围成的多面体,半正多面体体现了数学的对称美.如图是一个棱数为24的半正多面体,其棱长为 , 则该半正多面体的表面积为 , 体积为 .

三、解答题
-
17. 已知数列满足: , , 且 .(1)、求证:数列为等差数列;(2)、若数列满足 , 求数列的通项公式.18. 在中,a,b,c分别为角A,B,C所对的边,已知 , .(1)、求角A及的值;(2)、若D为AB边上一点,且 , , 求的面积.19. 已知函数 .(1)、讨论函数的单调性;(2)、若函数有两个零点,求a的取值范围.20. 如图,在四棱锥中,底面ABCD为菱形,点E在SD上,且 .
 (1)、若M,N分别为SA,SC的中点,证明:平面平面ACE;(2)、若 , , , 平面ABCD,求直线BS与平面ACE所成角的正弦值.
(1)、若M,N分别为SA,SC的中点,证明:平面平面ACE;(2)、若 , , , 平面ABCD,求直线BS与平面ACE所成角的正弦值.