广东省东莞市十校联考2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-02-23 类型:期末考试
一、单选题
-
1. 在以下永洁环保、绿色食品、节能、绿色环保四个标志中,是轴对称图形是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,不正确的选法是( )
2. 如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,不正确的选法是( ) A、∠ADB=∠ADC B、∠B=∠C C、DB=DC D、AB=AC3. 若式子有意义,则x的取值范围为( )A、x≥2 B、x≠3 C、x≤2或x≠3 D、x≥2且x≠34. 下列各式由左边到右边的变形中,是因式分解的是( )A、10x2﹣5x=5x(2x﹣1) B、x2﹣4x+4=x(x﹣4)+4 C、a(x+y)=ax+ay D、x2﹣16+3x=(x+4)(x﹣4)+3x5. 已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( )
A、∠ADB=∠ADC B、∠B=∠C C、DB=DC D、AB=AC3. 若式子有意义,则x的取值范围为( )A、x≥2 B、x≠3 C、x≤2或x≠3 D、x≥2且x≠34. 下列各式由左边到右边的变形中,是因式分解的是( )A、10x2﹣5x=5x(2x﹣1) B、x2﹣4x+4=x(x﹣4)+4 C、a(x+y)=ax+ay D、x2﹣16+3x=(x+4)(x﹣4)+3x5. 已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( ) A、4对 B、3对 C、2对 D、1对6. 如果等腰三角形的两边长分别为2和5,则它的周长为( )
A、4对 B、3对 C、2对 D、1对6. 如果等腰三角形的两边长分别为2和5,则它的周长为( )
A、9 B、7 C、12 D、9或127. 使分式的值为零的x的值是( )A、x=2 B、x=±2 C、x=﹣2 D、x=﹣2或x=﹣18. 到三角形三边距离相等的点是( )A、三边垂直平分线的交点 B、三条高所在直线的交点 C、三条角平分线的交点 D、三条中线的交点9. 张老师和李老师同时从学校出发,步行15千米去县城购买书籍,张老师比李老师每小时多走1千米,结果比李老师早到半小时,两位老师每小时各走多少千米?设李老师每小时走x千米 ,依题意,得到的方程是( )A、 B、 C、 D、10. 如图,在边长为a的正方形中挖掉一个边长为b的小正方形 , 把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )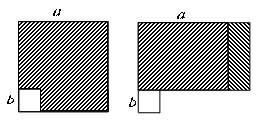 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: -9= .12. 三角形的三边长分别为5,1+2x,8,则x的取值范围是.13. 等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为 .14. 如图,点P关于OA,OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,若CD=18cm,则△PMN的周长为cm.
 15. 如图:在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为;
15. 如图:在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为; 16.
16.如图,边长为m+4的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形,若拼成的矩形一边长为4,则另一边长为 .
 17. 若一个整数能表示成a2+b2(a,b是整数)的形式,则称这个数为“完美数”.
17. 若一个整数能表示成a2+b2(a,b是整数)的形式,则称这个数为“完美数”.例如,因为5=22+12 , 所以5是一个“完美数”.
(1)、请你再写一个大于10且小于20的“完美数”;(2)、已知M是一个“完美数”,且M=x2+4xy+5y2﹣12y+k(x,y是两个任意整数,k是常数),则k的值为 .三、解答题
-
18. 解分式方程:=3.19. 先化简,再求值:已知 , 求的值.20. 如图,在△ABC中,AB=AC,AD⊥BC,∠BAD=40°,AD=AE,求∠CDE的度数.
 21. 如图,某市有一块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
21. 如图,某市有一块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像. (1)、试用含a,b的代数式表示绿化的面积是多少平方米?(2)、若a=3,b=2,请求出绿化面积.22. 如图,在Rt△ABC中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P点作PF⊥AD交BC的延长线于点F,交AC于点H.
(1)、试用含a,b的代数式表示绿化的面积是多少平方米?(2)、若a=3,b=2,请求出绿化面积.22. 如图,在Rt△ABC中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P点作PF⊥AD交BC的延长线于点F,交AC于点H. (1)、∠APB的度数为°;(2)、求证:△ABP≌△FBP;(3)、求证:AH+BD=AB.23. 某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的3倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需10天.(1)、这项工程的规定时间是多少天?(2)、已知甲队每天的施工费用为6500元,乙队每天的施工费用为3900元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?24. 如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE.
(1)、∠APB的度数为°;(2)、求证:△ABP≌△FBP;(3)、求证:AH+BD=AB.23. 某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的3倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需10天.(1)、这项工程的规定时间是多少天?(2)、已知甲队每天的施工费用为6500元,乙队每天的施工费用为3900元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?24. 如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE. (1)、若点D是AC的中点,如图1,求证:AD=CE(2)、若点D不是AC的中点,如图2,试判断AD与CE的数量关系,并证明你的结论:(提示:过点D作DF∥BC , 交AB于点F)25. 如图
(1)、若点D是AC的中点,如图1,求证:AD=CE(2)、若点D不是AC的中点,如图2,试判断AD与CE的数量关系,并证明你的结论:(提示:过点D作DF∥BC , 交AB于点F)25. 如图 (1)、如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,线段EF、BE、FD之间的关系是;(不需要证明)(2)、如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.(3)、如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
(1)、如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,线段EF、BE、FD之间的关系是;(不需要证明)(2)、如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.(3)、如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.