上海市宝山区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-02-23 类型:期末考试
一、填空题
-
1. 用代数式表示:x和y的平方和 .2. 多项式中的常数项是 .3. 计算: .4. 计算:(a3)2= .5. 计算: .6. 分解因式: .7. 如果分式有意义,那么的取值范围是 .8. 将写成不含分母的形式,其结果为 .9. 1秒是1微秒的1000000倍,那么3微秒可以用科学记数法记作秒.10. 计算: .11. 如果关于x的方程2+3x-m=0无解,那么m的取值范围是 .12. 如图,是由通过平移得到,且点在同一条直线上,如果 , . 那么这次平移的距离是 .
 13. 长方形纸片按图中方式折叠,其中为折痕,如果折叠后在一条直线上,那么的大小是度.
13. 长方形纸片按图中方式折叠,其中为折痕,如果折叠后在一条直线上,那么的大小是度.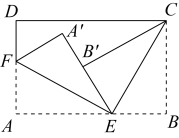 14. 如图,已知的三个角, , , , 将绕点顺时针旋转得到 , 如果 , 那么 .
14. 如图,已知的三个角, , , , 将绕点顺时针旋转得到 , 如果 , 那么 . 15. 计算: .
15. 计算: .二、单选题
-
16. 下列运算正确的是( )A、 B、 C、 D、17. 已知分式的值为 , 如果把分式中的同时扩大为原来的3倍,那么新得到的分式的值为( )A、 B、 C、 D、18. 下列说法正确的是( )A、轴对称图形是由两个图形组成的 B、等边三角形有三条对称轴 C、两个等面积的图形一定轴对称 D、直角三角形一定是轴对称图形19. 顺次连接正六边形的三个不相邻的顶点得到如图的图形,该图形( )
 A、既是轴对称图形也是中心对称图形 B、是轴对称图形但并不是中心对称图形 C、是中心对称图形但并不是轴对称图形 D、既不是轴对称图形也不是中心对称图形20. 已知并排放置的正方形和正方形如图,其中点在直线上,那么的面积和正方形的面积的大小关系是( )
A、既是轴对称图形也是中心对称图形 B、是轴对称图形但并不是中心对称图形 C、是中心对称图形但并不是轴对称图形 D、既不是轴对称图形也不是中心对称图形20. 已知并排放置的正方形和正方形如图,其中点在直线上,那么的面积和正方形的面积的大小关系是( ) A、 B、 C、 D、
A、 B、 C、 D、三、解答题
-
21. 计算:22. 分解因式:23. 分解因式:24. 解方程:25. 计算:(计算结果不含负指数)26. 小明在进行两个多项式的乘法运算时,不小心把乘错抄成除以 , 结果得到 , 如果小明没有错抄题目,并且计算依然符合题意,那么得到的结果应该是什么?27. 如图,在4×4的方格中,的三个顶点都在格点上.
 (1)、在图1中画出与关于点中心对称的;(2)、在图2中画出与关于直线轴对称的;(3)、在图3中画出绕着点按顺时针方向旋转后的 .28. 先化简,再求值: , 其中为满足 .29. 如果的三边长满足等式 , 试判断此的形状并写出你的判断依据.30. 元旦,小红和弟弟小杰两人以包馄饨来庆祝成长,两人实际所包的馄饨数之比是5:3(小红:小杰),调皮的弟弟小杰从小红包好的馄饨里拿了2个放入自己的成果行列后,宣称自己和姐姐包好的馄饨数之比是2:3,求两人一共所包的馄饨数.(列分式方程解应用题)31. 数学兴趣小组的同学发现:一些复杂的图形运动是由若干个图形基本运动组合形成的,如一个图形沿一条直线翻折后再沿这条直线的方向平移,这样的一种图形运动,大家讨论后把它称为图形的“翻移运动”,这条直线则称为(这次运动的)“翻移线”如图1,就是由沿直线1翻移后得到的.(先翻折,然后再平移)
(1)、在图1中画出与关于点中心对称的;(2)、在图2中画出与关于直线轴对称的;(3)、在图3中画出绕着点按顺时针方向旋转后的 .28. 先化简,再求值: , 其中为满足 .29. 如果的三边长满足等式 , 试判断此的形状并写出你的判断依据.30. 元旦,小红和弟弟小杰两人以包馄饨来庆祝成长,两人实际所包的馄饨数之比是5:3(小红:小杰),调皮的弟弟小杰从小红包好的馄饨里拿了2个放入自己的成果行列后,宣称自己和姐姐包好的馄饨数之比是2:3,求两人一共所包的馄饨数.(列分式方程解应用题)31. 数学兴趣小组的同学发现:一些复杂的图形运动是由若干个图形基本运动组合形成的,如一个图形沿一条直线翻折后再沿这条直线的方向平移,这样的一种图形运动,大家讨论后把它称为图形的“翻移运动”,这条直线则称为(这次运动的)“翻移线”如图1,就是由沿直线1翻移后得到的.(先翻折,然后再平移)

 (1)、在学习中,兴趣小组的同学就“翻移运动”对应点(指图1中的与 , 与…)连线是否被翻移线平分发生了争议.对此你认为如何?(直接写出你的判断)(2)、如图2,在长方形中, , 点分别是边中点,点在边延长线上,联结 , 如果是经过“翻移运动”得到的三角形.请在图中画出上述“翻移运动”的“翻移线”直线;联结 , 线段和直线交于点 , 若的面积为3,求此长方形的边长的长.(3)、如图3,是(2)中的长方形边上一点,如果 , 先按(2)的“翻移线”直线翻折,然后再平移2个单位,得到 , 联结线段 , 分别和“翻移线”交于点和点 , 求四边形的面积.
(1)、在学习中,兴趣小组的同学就“翻移运动”对应点(指图1中的与 , 与…)连线是否被翻移线平分发生了争议.对此你认为如何?(直接写出你的判断)(2)、如图2,在长方形中, , 点分别是边中点,点在边延长线上,联结 , 如果是经过“翻移运动”得到的三角形.请在图中画出上述“翻移运动”的“翻移线”直线;联结 , 线段和直线交于点 , 若的面积为3,求此长方形的边长的长.(3)、如图3,是(2)中的长方形边上一点,如果 , 先按(2)的“翻移线”直线翻折,然后再平移2个单位,得到 , 联结线段 , 分别和“翻移线”交于点和点 , 求四边形的面积.