山东省济宁市高新区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个图形中，不是轴对称图形的为（　　）

A、 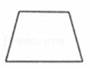B、 C、 D、

查看试题解析
2. （﹣ $\frac{1}{4}$ ）²的平方根是（　　）

A、﹣ $\frac{1}{4}$ B、 $\frac{1}{4}$ C、± $\frac{1}{4}$ D、± $\frac{1}{2}$

查看试题解析
3. 下列长度的三条线段能组成三角形的是（）

A、3，6，9 B、5，6，8 C、1，2，4 D、5，6，15

查看试题解析
4. 已知函数y＝（m﹣2） $x^{m^{2} - 3}$ ＋1是一次函数，则m的值为（）

A、± $\sqrt{3}$ B、 $\sqrt{3}$ C、±2 D、﹣2

查看试题解析
5. 一次函数y＝kx+b的图象如图所示，则点（k，﹣b）在第（）象限内．

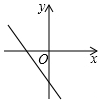A、一 B、二 C、三 D、四

查看试题解析
6. 已知点（﹣1，y₁），（4，y₂）在一次函数y＝3x+a的图象上，则y₁ ， y₂的大小关系是（）

A、y₁＜y₂ B、y₁＝y₂ C、y₁＞y₂ D、不能确定

查看试题解析
7. 点P（m+3，m-1）；在y轴上，则点P的坐标为（）

A、（0，-4） B、（5，0） C、（0，5） D、（-4，0）

查看试题解析
8. 如图，以 $R t △ A B C$ 的三边为直径分别向外作半圆，若斜边 $A B = 3$ ，则图中阴影部分的面积为（）

A、 $9 π$ B、 $\frac{9}{2} π$ C、 $\frac{9}{4} π$ D、 $3 π$

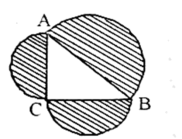查看试题解析
9. A、B两地相距80km，甲、乙两人沿同一条路从A地到B地．l₁ ， l₂分别表示甲、乙两人离开A地的距离s（km）与时间t（h）之间的关系．对于以下说法：①乙车出发1.5小时后甲才出发；②两人相遇时，他们离开A地20km；③甲的速度是40km/h，乙的速度是 $\frac{40}{3}$ km/h；④当乙车出发2小时时，两车相距13km．其中正确的结论是（）

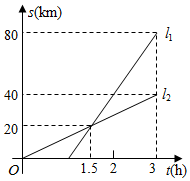A、①③ B、①④ C、②③ D、②④

查看试题解析
10. 对于实数a、b，定义min{a，b}的含义为：当a＜b时，min{a，b}＝a；当a＞b时，min{a，b}＝b，例如：min{1，﹣2}＝﹣2.已知min{ $\sqrt{30}$ ，a}＝a，min{ $\sqrt{30}$ ，b}＝ $\sqrt{30}$ ，且a和b为两个连续正整数，则2a﹣b的值为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11.
小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形？应该带第块．

查看试题解析
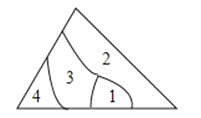12. 如图，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”，踩伤了花草．则他们仅仅少走了步路．（假设2步为1米）

查看试题解析
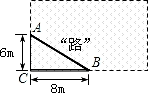13. 如图，△ABC中，DE垂直平分边AC，若BC＝8，AB＝10，则△EBC的周长为．

查看试题解析
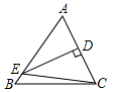14. 已知a是 $\sqrt{10}$ 的整数部分，b是它的小数部分，则 ${(- a)}^{3} + {(b + 3)}^{2}$ = ．

查看试题解析
15. 将一次函数 $y = 3 x + 2$ 的图象进行上下平移，使得平移之后的图象经过点 $A (4 ， 3)$ ，则平移之后图象的解析式为．

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt{25} - \sqrt[3]{64} - {(- 1)}^{2021}$ ；

(2)、 $| \sqrt{3} - 2 | - \sqrt{{(- 3)}^{2}} - \sqrt[3]{- 27}$ .

查看试题解析
17. 已知x+1的平方根是±2，2x+y﹣2的立方根是2，求x²+y²的算术平方根．

查看试题解析
18. 如图，在△ABC 和△DBC 中，∠ACB＝∠DBC＝90°，点 E 是 BC 的中点，DE⊥AB 于点F，且 AB＝DE．

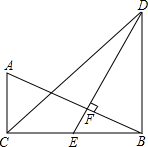(1)、求证：△ACB≌△EBD；

(2)、若 DB＝12，求 AC 的长．

查看试题解析
19. 一架云梯长25m，如图那样斜靠在一面墙上，云梯顶端离地面24m．

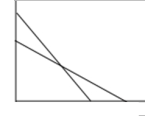(1)、这架云梯的底端距墙角有多远?

(2)、如果云梯的顶端下滑了4m，那么它的底部在水平方向滑动了多少m？

查看试题解析
20. 如图，在平面直角坐标系中，已知点A（2，﹣2），点P是x轴上的一个动点．

(1)、A₁ ， A₂分别是点A关于原点的对称点和关于y轴对称的点，直接写出点A₁ ， A₂的坐标，并在图中描出点A₁ ， A₂ ．

(2)、求使△APO为等腰三角形的点P的坐标．

查看试题解析
21. 某电信公司手机通讯有两种收费方式：（A）计时制：0.5元/min；（B）包月制：月租12元，另外通话费按0.2元/min．

(1)、写出两种方式每月应缴费用y（元）与通话时间x（min）之间的关系式．

(2)、某手机用户平均每个月通话时间为60min，他采用哪种方式较合算？为什么？

(3)、如果该用户本月预缴了100元的话费，按包月制算，该用户本月可通话多长时间？

查看试题解析
22. 如图，已知直线y＝﹣ $\frac{3}{4}$ x+3与x轴、y轴分别相交于点A、B，将△AOB沿直线CD折叠，使点A与点B重合．折痕CD与x轴交于点C，与AB交于点D．

(1)、点A的坐标为，点B的坐标为；

(2)、求OC的长度，并求出此时直线BC的表达式；

(3)、过点B作直线BP与x轴交于点P，且使OP＝ $\frac{1}{2}$ OA，求△ABP的面积．

查看试题解析