山东省济南市长清区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-23 类型：期末考试

进入出卷网下载

一、单选题

1. －5的相反数是（）

A、－5 B、－ $\frac{1}{5}$ C、5 D、1

查看试题解析
2. 如图所示的几何体，它的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 12月9日从北京冬奥委组获悉，北京2022年冬奥会和冬残奥会志愿者全球招募启动以来，报名非常踊跃，报名人数已达463000，数字463000用科学记数法表示为（）

A、 $4.63 \times 1 0^{2}$ B、 $4.63 \times 1 0^{3}$ C、 $4.63 \times 1 0^{4}$ D、 $4.63 \times 1 0^{5}$

查看试题解析
4. 下列调查中，适合用抽样调查的是（）

A、调查一批防疫口罩的质量情况 B、对乘坐高铁的乘客进行安检 C、对新研发导弹的零部件进行检查 D、防疫期间对进入校园的人员进行体温检测

查看试题解析
5. 已知- $5 x^{a} y^{3}$ 与 $2 x^{2} y^{b}$ 为同类项，则 $a^{b}$ 的值为（）

A、2 B、4 C、6 D、8

查看试题解析
6. 下列运算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $3 a b - a b = 2$ C、 $3 a b^{2} - 5 a b^{2} = - 2 a b$ D、 $3 a - 2 a = a$

查看试题解析
7. 已知x＝3是关于x的方程3x+2a＝1的解，那么a的值为（）

A、﹣4 B、4 C、﹣5 D、5

查看试题解析
8. 如图，两块三角板的直角顶点O重合在一起， $∠ B O D = 35 °$ ，则 $∠ A O C$ 的度数为（）

A、 $35 °$ B、 $45 °$ C、 $55 °$ D、 $65 °$

查看试题解析
9. 党的十八大以来，我国实施精准扶贫精准脱贫，全面打响了脱贫攻坚战，扶贫工作取得了决定性进展．如图的统计图反映了我国五年来农村贫困人口的相关情况，其中“贫困发生率”是指贫困人口占目标调查人口的百分比．根据统计图提供的信息，下列推断中不合理的是（）

A、与2018年相比，2019年年末全国农村贫困人口减少了1109万人 B、 $2015 ~ 2019$ 年年末，与上一年相比，全国农村贫困人口的减少量均超过1000万 C、 $2015 ~ 2019$ 年年末，与上一年相比，全国农村贫困发生率逐年下降 D、 $2015 ~ 2019$ 年年末，与上一年相比，全国农村贫困发生率下降均不少于 $1.2 %$

查看试题解析
10. 《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数，物价各几何？“译文：“几个人一起去购买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱，问有多少人，物品的价格是多少？”设有x人，可列方程为（）

A、 $8 x - 3 = 7 x + 4$ B、 $8 x - 3 = 7 x - 4$ C、 $8 x + 3 = 7 x + 4$ D、 $8 x + 3 = 7 x - 4$

查看试题解析
11. 一个商标图案如图中阴影部分，在长方形ABCD中，AB＝4cm，BC＝2cm，以点A为圆心，AD为半径作圆与BA的延长线相交于点F，则商标图案的面积是（）

A、 $(π + 2) c m^{2}$ B、 $(π + 4) c m^{2}$ C、 $(2 π + 4) c m^{2}$ D、 $(3 π + 6) c m^{2}$

查看试题解析
12. 如图所示的数码叫“莱布尼茨调和三角形”，它们是由整数的倒数组成的，第 $n$ 行有 $n$ 个数，且两端的数均为 $\frac{1}{n}$ ，每个数是它下一行左右相邻两数的和，则第9行第3个数(从左往右数)为（）

A、 $\frac{1}{60}$ B、 $\frac{1}{168}$ C、 $\frac{1}{252}$ D、 $\frac{1}{280}$

查看试题解析

二、填空题

13. －|－3|＝．

查看试题解析
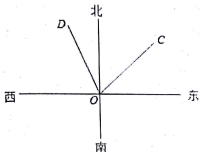
14. 过某个多边形的一个顶点的所有对角线，将这个多边形分成6个三角形，这个多边形是边形．

查看试题解析
15. 若 $a - b = - 1$ ，则 $3 a - 3 b + 1$ 的值是．

查看试题解析
16. 如图，已知点C在点O的北偏东 $4 5^{∘}$ 方向，点D在点O的北偏西 $2 0^{∘}$ 方向，那么∠COD为度．

查看试题解析
17. 一件衬衫按进价提高50%后进行标价，后因季节原因要按标价的8折出售，每件以72元卖出，则这批衬衫的进价是每件元．

查看试题解析
18. 如图，长方形ABCD点E，F分别在边AB，CD上，连接EF将∠BEF对折，点B落在直线EF上的点 $B$ 处，得折痕EM；将∠AEF对折，点A落在直线EF上的点 $A$ 处，得折痕EN，点G在CD上， $∠ N E G = 2 ∠ M E G ， ∠ F E G = 3 ∠ A E N$ ，则∠BEM为度．

查看试题解析

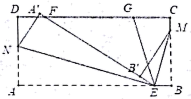
三、解答题

19. 计算题

(1)、 $(- \frac{1}{3}) - 15 + (- \frac{2}{3})$

(2)、 $- 1^{2} + 6 \div (- 2) \times (- \frac{1}{3})$

查看试题解析
20. 如图，已知四点A，B，C，D，请用直尺按要求完成作图，

(1)、作射线AD；

(2)、作直线BC；

(3)、连接BD，请在BD上确定点P，使 $A P + C P$ 的值最小，依据是．

查看试题解析
21. 已知：如图，点A、B、C、D四点共线，AC＝2BC，BC＝3，D为AB中点，求CD的长．

查看试题解析
22. 化简

(1)、化简： $3 a + 2 b - (5 a - b$ ）

(2)、先化简、再求值： $- 2 (4 x^{2} - 2 x + 8) - (4 x - 1)$ ，其中 $x = 1$ ．

查看试题解析
23. 解方程：

(1)、 $5 x - 2 = 7 x + 8$

(2)、 $\frac{2 x - 1}{3} = \frac{x + 2}{2} - 1$

查看试题解析
24. 本学期某学校开展以“庆百年建党”为主题的研学活动，组织120名学生参观山东省党史馆和济南战役纪念馆，每一名学生只能参加其中一项活动，学校租车一次性支付车票2200元．车票信息如下：
地点
票价
山东省党史馆
20元/人
济南战役纪念馆
16元/人

(1)、请问参观山东省党史馆和济南战役纪念馆的人数各是多少人？

(2)、若学生都去参观济南战役纪念馆，则能节省车票票款多少元？

查看试题解析
25. 为进一步提高课后服务质量，将“双减”政策落地，某校利用课外活动时间开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程．为了解八年级学生对每类课程的选择情况，随机抽取了八年级若干名学生进行调查（每人必选且只选一类最喜欢的课程），将调查结果绘制成如图所示的两幅不完整的统计图．
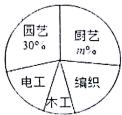
请根据统计图提供的信息，解答下列问题：

(1)、本次共调查了名学生；

(2)、补全条形统计图：

(3)、扇形统计图中，m的值为；“编织”所对应的圆心角的度数为；

(4)、若该校八年级共有1000名学生，请估计该校八年级学生选择“电工”劳动课的人数．

查看试题解析
26. 如图，以直线AB上一点O为端点作射线OC，使 $∠ B O C = 70 °$ ，将一个直角三角形的直角顶点放在点O处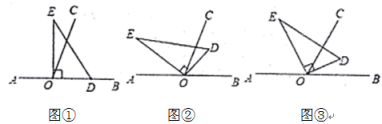， $∠ D O E = 90 °$ ．

(1)、如图①，若直角三角板DOE的一边OD放在射线OB上，则∠COE＝；

(2)、如图②，将直角三角板DOE绕点O逆时针方向转动到某个位置，若OC恰好平分∠BOE，求∠COD的度数；

(3)、如图③，将直角三角板DOE绕点O转动，如果OD始终在∠BOC的内部，试猜想∠BOD和∠COE有怎样的数量关系？并说明理由．

查看试题解析
27. 在数轴上，点M、N表示的数分别为m、n，那么M、N两点之间的距离为 $M N = | m - n |$ ；反过来，式子 $| m - n |$ 的几何意义是：数轴上表示数m的点和表示数n的点之间的距离．
已知点A在数轴上表示的数是a，点B表示的数为b，且满足 $| a + 3 | + {(b - 5)}^{2} = 0$ ．

(1)、a＝， b＝， AB＝．（直接写出结果）

(2)、如图1，点P是数轴上一点，点P到点A的距离是点P到点B的距离的3倍（即PA＝3PB），求点P在数轴上表示的数；

(3)、如图2，点M，N分别从点O，B同时出发，分别以 $v_{1}$ ， $v_{2}$ 的速度沿数轴负方向运动（M在O，A之间，N在O，B之间），运动时间为t秒，点Q为O，N之间一点，且点Q到N的距离是点A到N的距离的一半（即 $Q N = \frac{1}{2} A N$ ），若M，N运动过程中Q到M的距离（即QM）总为一个固定的值，写出 $v_{1}$ 与 $v_{2}$ 的数量关系，并说明理由．

查看试题解析

地点	票价
山东省党史馆	20元/人
济南战役纪念馆	16元/人