江西省宜春市2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-23 类型：期末考试

进入出卷网下载

一、单选题

1. 2021的相反数是（）

A、 $- 2021$ B、 $- \frac{1}{2021}$ C、2021 D、 $\frac{1}{2021}$

查看试题解析
2. 下列运算正确的是（）

A、 $3 a - 2 a = 1$ B、 $2 a^{2} + 3 a^{3} = 5 a^{5}$ C、 $7 a^{3} - 3 a^{3} = 4 a^{3}$ D、 $2^{2021} - 2^{2020} = 2$

查看试题解析
3. 上午8：30时，时针和分针所夹锐角的度数是（）

A、75° B、80° C、70° D、67.5°

查看试题解析
4. 一个立体图形由若干个完全相同的正方体构成，如图是分别从正面、左面、上面观察这个图形得到的视图这个立体图形由多少个正方体组成？（）

A、8 B、9 C、10 D、无法判断

查看试题解析
5. 若方程 $(m - 1) x^{| m - 2 |} - 8 = 0$ 是关于x的一元一次方程，则 $m =$ （）

A、1 B、2 C、3 D、1或3

查看试题解析
6. 将一副三角板如图①的位置摆放，其中30°直角三角板的直角边与等腰直角三角板的斜边重合，30°直角三角板直角顶点与等腰直角三角板的锐角顶点重合（为点O）．现将30°的直角三角板绕点O顺时针旋转至如图②的位置，此时 $∠ 1 = 20 °$ ，则 $∠ 2 =$ （）

A、30° B、25° C、20° D、15°

查看试题解析

二、填空题

7. 如果单项式 $3 x^{m} y$ 与 $- 5 x^{3} y^{n}$ 的和仍是单项式，那么 $m + n =$ .

查看试题解析
8. 第七次全国人口普查结果公布，宜春市常住人口总数大约为501万人，把数字501万用科学记数法表示为

查看试题解析
9. 一个角比它的补角的3倍多40°，则这个角的度数为．

查看试题解析
10. 七年级部分学生去某处旅游，如果每辆汽车坐30人，那么有15个学生没有座位；如果每辆汽车坐45人，那么空出1辆汽车．若设有x辆汽车，则可列方程为．

查看试题解析
11. 按一般规律排列的一列数依次为： $\frac{1}{2}$ ， $\frac{1}{3}$ ， $\frac{1}{10}$ ， $\frac{1}{15}$ ， $\frac{1}{26}$ ， $\frac{1}{35}$ ……，按此规律排列下去，这列数中的第2021个数是．

查看试题解析
12. 已知线段AC，点D为AC的中点，B是直线AC的一点，且 $B C = \frac{1}{3} A B$ ， $B D = 2 c m$ ，则 $A C =$ ．

查看试题解析

三、解答题

13.

(1)、 $- 1^{2} - [2 - {(- 3)}^{2}] \times | - \frac{1}{7} | \div (- \frac{1}{10})$

(2)、如图，OB，OE是 $∠ A O C$ 内的两条射线， $O D$ 平分 $∠ A O B$ ， $∠ B O E = \frac{1}{2} ∠ E O C$ ，若 $∠ D O E = 55 °$ ， $∠ A O C = 140 °$ ，求 $∠ E O C$ 的度数．

查看试题解析
14. 解方程：1 $- \frac{x - 13}{3} = \frac{9 - 3 x}{2} +$ x ．

查看试题解析
15. 按照下列语句画出图形．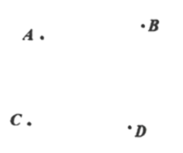

(1)、画直线AB；

(2)、画射线 $B D$ ；

(3)、连接BC；

(4)、反向延长线段CD至E，使 $D E = 2 C D$ ．

查看试题解析
16. 已知 $| a + 1 | + {(b - 2)}^{2} = 0$ ，先化简，再求值： $(2 a^{3} - 2 b^{2}) - 3 (a^{3} b^{2} + a^{3}) + 2 (b^{2} + b^{2} a^{3})$ ．

查看试题解析
17. 如图，有理数a，b，c在数轴上的对应点分别是A，B，C，原点为点O．

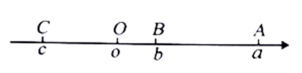(1)、化简： $| a - c | + | c - b | - | b - a |$ ．

(2)、若B为线段AC的中点， $O A = 8$ ， $O A = 4 O B$ ，求c的值．

查看试题解析
18. 定义新运算“@”与“ $\oplus$ ”： $a @ b = \frac{a + b}{2}$ ， $a \oplus b = \frac{a - b}{2}$

(1)、计算 $3@ (- 2) - (- 2) \oplus (- 1)$ 的值；

(2)、若 $A = 3 b @ (- a) + a \oplus (2 - 3 b) ， B = a @ (- 3 b) + (- a) \oplus (- 2 - 9 b)$ ，比较A和B的大小

查看试题解析
19. 开学发新书，两摞规格相同的数学新课本如图所示，整齐地叠放在课桌上，请根据图中所给的数据信息，解答下列问题：

(1)、每本数学新课本的厚度为厘米；

(2)、当数学新课本数为x（本）时，请直接写出同样叠放在桌面上的一摞数学新课本最上面高出地面的距离（用含x的代数式表示）；

(3)、如果有一个班级的学生每人要领取1本数学新课本，全班的数学新课本放在桌面上，班级中 $\frac{2}{3}$ 的学生领取后，桌上剩余的数学新课本整齐地摆放成一摞，课本最上面高出地面的距离为96.8厘米，你能从中知道该班学生的人数吗？请说出理由.

查看试题解析
20. 某商店对甲、乙两种商品在进价的基础上提高50%作为标价出售．春节期间，该商店对甲、乙两种商品开展促销活动，活动方案如下：
商品
甲
乙
标价（元/件）
150
225
春节期间每件商品出售的价格
按标价降价10%
按标价降价a%

(1)、商品乙降价后的售价为元（用含a的代数式表示）；

(2)、不考虑其他成本，在春节期间商店卖出商品甲20件，商品乙10件，获得总利润1000元，试求a的值．

查看试题解析
21. 已知 $∠ A O B$ 和 $∠ C O D$ 是直角．

(1)、如图1，当射线 $O B$ 在 $∠ C O D$ 内部时，请探究 $∠ A O D$ 和 $∠ B O C$ 之间的关系，并总明理由．

(2)、如图2，当射线 $O A$ ， $O B$ 都在 $∠ C O D$ 的外部时，过点 $O$ 作射线 $O E$ ， $O F$ ，满足 $∠ B O E = \frac{1}{4} ∠ B O C$ ， $∠ D O F = \frac{3}{4} ∠ A O D$ ，求 $∠ E O F$ 的度数．

(3)、在（2）的条件下，在平面内是否存在射线 $O G$ ，使得 $∠ G O F ： ∠ G O E = 3 ： 7$ ？若存在，请直接写出 $∠ G O F$ 的度数；若不存在，请说明理由．

查看试题解析

商品	甲	乙
标价（元/件）	150	225
春节期间每件商品出售的价格	按标价降价10%	按标价降价a%