广东省中山市2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-02-23 类型:期末考试
一、单选题
-
1. ﹣2的相反数是( )A、﹣ B、 C、2 D、﹣22. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.根据刘徽的这种表示法,图1表示的数值为:(+1)+(﹣1)=0,则可推算图2表示的数值为( )
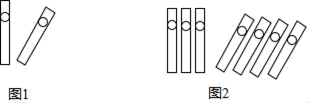 A、7 B、﹣1 C、1 D、±13. “一带一路”建设将促进我国与世界一些国家的互利合作,“一带一路”地区复盖总人口约为4400000000人,这个数用科学记数法表示为( )A、4.4×109 B、44×108 C、0.44×1010 D、440×1074. 下列四个数中,最小的数是( )A、﹣3 B、|﹣7| C、﹣(﹣1) D、﹣5. 下列各组式子中是同类项的是( )A、2x3与3x2 B、12ax与8bx C、x4与a4 D、23与326. 某商店促销的方法是将原价x元的衣服以(0.8x﹣10)元出售,意思是( )A、原价减去10元后再打8折 B、原价打8折后再减去10元 C、原价减去10元后再打2折 D、原价打2折后再减去10元7. 下列各式变形正确的是( )A、由得 B、由得 C、由得 D、由得8. 下列平面展开图是由5个大小相同的正方形组成,其中沿正方形的边不能折成无盖小方盒的是( )A、
A、7 B、﹣1 C、1 D、±13. “一带一路”建设将促进我国与世界一些国家的互利合作,“一带一路”地区复盖总人口约为4400000000人,这个数用科学记数法表示为( )A、4.4×109 B、44×108 C、0.44×1010 D、440×1074. 下列四个数中,最小的数是( )A、﹣3 B、|﹣7| C、﹣(﹣1) D、﹣5. 下列各组式子中是同类项的是( )A、2x3与3x2 B、12ax与8bx C、x4与a4 D、23与326. 某商店促销的方法是将原价x元的衣服以(0.8x﹣10)元出售,意思是( )A、原价减去10元后再打8折 B、原价打8折后再减去10元 C、原价减去10元后再打2折 D、原价打2折后再减去10元7. 下列各式变形正确的是( )A、由得 B、由得 C、由得 D、由得8. 下列平面展开图是由5个大小相同的正方形组成,其中沿正方形的边不能折成无盖小方盒的是( )A、 B、
B、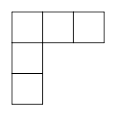 C、
C、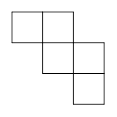 D、
D、 9. 下列说法正确的是( )A、线段AB和线段BA表示的不是同一条线段 B、射线AB和射线BA表示的是同一条射线 C、若点P是线段AB的中点,则PA=AB D、线段AB叫做A、B两点间的距离10. 如图,数轴上点A表示的有理数为a,下列各数中在0,1之间的是( )
9. 下列说法正确的是( )A、线段AB和线段BA表示的不是同一条线段 B、射线AB和射线BA表示的是同一条射线 C、若点P是线段AB的中点,则PA=AB D、线段AB叫做A、B两点间的距离10. 如图,数轴上点A表示的有理数为a,下列各数中在0,1之间的是( ) A、a B、﹣a C、|a|﹣1 D、a+1
A、a B、﹣a C、|a|﹣1 D、a+1二、填空题
-
11. 若∠α=70°,则它的补角是.12. 已知关于x的方程2x+a﹣9=0的解是x=2,则a的值为 .13. 已知a2+2a﹣3=0,则代数式2a2+4a﹣3的值是 .14. 用符号max(a,b)表示a,b两数中的较大者,用符号min(a,b)表示a,b两数中的较小者,则maxmin的值为 .15. 如图,点C在线段AB上,D是线段AC的中点,若CB=2,CD=3CB,则线段AB的长 .
 16. 我国《洛书》中记载着世界上最古老的一个幻方:将1~9这九个数字填入3×3的方格内,使每一行、每一列、两条对角线上的三个数之和都相等.如图的幻方中,m= .
16. 我国《洛书》中记载着世界上最古老的一个幻方:将1~9这九个数字填入3×3的方格内,使每一行、每一列、两条对角线上的三个数之和都相等.如图的幻方中,m= . 17. 我们知道,无限循环小数可以转化为分数,例如转化为分数时,可设=x,则=10x,两式相减得3=9x,解得 , 即 , 则转化为分数是 .
17. 我们知道,无限循环小数可以转化为分数,例如转化为分数时,可设=x,则=10x,两式相减得3=9x,解得 , 即 , 则转化为分数是 .三、解答题
-
18. 计算: .19. 先化简,再求值: 其中20. 解方程: =1.21. 如图,已知平面上有四个村庄,用四个点A,B,C,D表示.
 (1)、连接AB,作射线AD,作直线BC与射线AD交于点E;(2)、若要建一供电所M,向四个村庄供电,要使所用电线最短,则供电所M应建在何处?请画出点M的位置并说明理由.22. 小奇借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=ab+2a.(1)、求的值;(2)、若⊕x=x⊕3,求x的值.23. 仔细观察下列三组数:
(1)、连接AB,作射线AD,作直线BC与射线AD交于点E;(2)、若要建一供电所M,向四个村庄供电,要使所用电线最短,则供电所M应建在何处?请画出点M的位置并说明理由.22. 小奇借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=ab+2a.(1)、求的值;(2)、若⊕x=x⊕3,求x的值.23. 仔细观察下列三组数:第一组:1,﹣4,9,﹣16,25,……
第二组:0,﹣5,8,﹣17,24,……
第三组:0,10,﹣16,34,﹣48,……
根据它们的规律,解答下列问题:
(1)、取每组数的第10个数,计算它们的和;(2)、取每组数的第n个数,它们的和能否是﹣1,说明理由.24. 如表是某校七~九年级某月课外兴趣小组活动时间统计表,已知各年级同一兴趣小组每次活动时间相同,文艺小组每次活动时间比科技小组每次活动时间多0.5小时.请根据表中信息解答:年级
文艺小组与科技小组活动总时间(小时)
文艺小组活动次数
科技小组活动次数
七年级
12.5
4
3
八年级
10.5
3
a
九年级
7
m
n
(1)、求文艺小组每次活动的时间;(2)、求a的值;(3)、直接写出结果:m=;n= .25. 如图1,已知∠AOB=150°,∠COE与∠EOD互余,OE平分∠AOD. (1)、在图1中,若∠COE=32°,求∠BOD的度数;(2)、在图1中,设∠COE=α,∠BOD=β,请探索α与β之间的数量关系;(3)、已知条件不变,当∠COD绕点O逆时针转动到如图2的位置时,(2)中α与的数量关系是否仍然成立?若成立,请说明理由;若不成立,请探索α与β之间的数量关系.
(1)、在图1中,若∠COE=32°,求∠BOD的度数;(2)、在图1中,设∠COE=α,∠BOD=β,请探索α与β之间的数量关系;(3)、已知条件不变,当∠COD绕点O逆时针转动到如图2的位置时,(2)中α与的数量关系是否仍然成立?若成立,请说明理由;若不成立,请探索α与β之间的数量关系.