广东省佛山市南海区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-02-23 类型:期末考试
一、单选题
-
1. 比-1小的数是( )A、0 B、 C、-0.5 D、-22. 若气温升高时,记作 , 则气温下降时,记作( )A、 B、 C、 D、3. 下列各式,正确的是( )A、2a+3b=5ab B、x+2x=3x C、2(a+b)=2a+b D、-(m-n)=-m+n4. 下列调查最适合用普查的是( )A、了解七年级1班每位学生身高情况 B、检测一款新手机的待机时长 C、了解全国中学生最喜爱的图书种类 D、调查全市人民对政府服务的满意程度5. 一个多边形从一个顶点引出的对角线条数是4条,这个多边形的边数是( )A、5 B、6 C、7 D、86. 若x=1是关于x的方程2x+a=0的解,则a的值为( )A、﹣1 B、﹣2 C、1 D、27. 如图, , , 平分 ,则 的度数为( )
 A、 B、 C、 D、8. 下列说法正确的是( )A、0是最小的有理数 B、若有理数m>n,则数轴上表示m的点一定在表示n的点的左边 C、一个有理数在数轴上表示的点离原点越远,这个有理数就越大 D、既没有最小的正数,也没有最大的负数.9. 下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
A、 B、 C、 D、8. 下列说法正确的是( )A、0是最小的有理数 B、若有理数m>n,则数轴上表示m的点一定在表示n的点的左边 C、一个有理数在数轴上表示的点离原点越远,这个有理数就越大 D、既没有最小的正数,也没有最大的负数.9. 下面四个图形中,经过折叠能围成如图所示的几何图形的是( ) A、
A、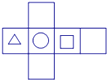 B、
B、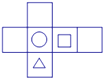 C、
C、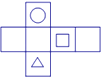 D、
D、 10. 如图,用同样大小的棋子按以下规律摆放,若第n个图中有2022枚棋子,则n的值是( )
10. 如图,用同样大小的棋子按以下规律摆放,若第n个图中有2022枚棋子,则n的值是( ) A、675 B、674 C、673 D、672
A、675 B、674 C、673 D、672二、填空题
-
11. 数轴上,将表示 的点向右移动3个单位后,对应点表示的数是 .12. 若方程和方程的解相同,则 .13. 用一个平面去截一个几何体,得到的截面是一个三角形,这个几何体可能是(写出一个即可);14. 如果3x2myn与﹣5x4y3是同类项,则代数式m-n的值为 .15. 计算: .16. 如图,把一张边长为的正方形纸板的四个角各剪去一个同样大小的正方形,再折成一个无盖的长方体盒子(纸板的厚度忽略不计),当剪去的正方形边长从变为后,长方体纸盒容积变小了 .
 17. 如图,点C是线段上任意一点(不与端点重合),点M是中点,点P是中点,点Q是中点,则下列说法:①;②;③;④ . 其中正确的是 .
17. 如图,点C是线段上任意一点(不与端点重合),点M是中点,点P是中点,点Q是中点,则下列说法:①;②;③;④ . 其中正确的是 .
三、解答题
-
18. 计算:19. 如图,是由6个大小相同的小立方体块搭建的几何体,请你在下方的指定方格中画出这个几何体从不同方向分别看到的图形:
 20. 解方程21. 先化简,再求值: , 其中 .22. 某校调查学生对“社会主义核心价值观”的内容了解情况,随机抽取部分学生进行问卷调查,问卷共设置“非常了解”、“比较了解”、“一般了解“不了解”四个选项,分别记为 , 根据调查结果绘制了如图尚不完整的统计图.
20. 解方程21. 先化简,再求值: , 其中 .22. 某校调查学生对“社会主义核心价值观”的内容了解情况,随机抽取部分学生进行问卷调查,问卷共设置“非常了解”、“比较了解”、“一般了解“不了解”四个选项,分别记为 , 根据调查结果绘制了如图尚不完整的统计图.
请解答下列问题:
(1)、本次问卷共随机调查了名学生,扇形统计图在D对应的圆心角为度.(2)、请补全条形统计图.(3)、若该校有1800名学生,估计该校选择“非常了解”的学生约有多少人?23. 为弘扬爱国主义精神,某校组织七年级学生以班级为单位观看电影《长津湖》,票价为每张40元,701班班长问售票员买团体票是否可以优惠,售票员说:“40人以上的团体票有两个优惠方案可选择,方案一:全体人员打8折;方案二:5人免票,其他人员打9折.”(1)、702班有41名学生,选择哪个方案更优惠?(2)、701班班长思考了一会儿说:“我们班无论选择哪种方案,要付的钱是一样多的.”请问701班有多少名学生?24. 某工厂计划用100张白板纸制作某种型号的长方体纸箱.如图,每张白板纸可以用三种方法中的一种剪裁,其中方法A:一张白板纸裁成5个侧面;方法B:一张白板纸裁成4个侧面与3个底面;方法C:一张白板纸裁成3个侧面与6个底面.且四个侧面和两个底面恰好能做成一个纸箱.设按方法A剪裁的有x张白板纸,按方法B剪裁的有y张白板纸. (1)、按方法C剪裁的有张白板纸.(用含的代数式表示)(2)、将100张白板纸裁剪完后,一共可以裁出多少个侧面与多少个底面?(用含的代数式表示,结果要化简)(3)、当时,最多可以制作该种型号的长方体纸箱多少个?25. 如图1,正方形和长方形的周长相等,且各有一条边在数轴上,点对应的数分别是 . 正方形以每秒2个单位长度的速度向右移动,同时长方形以每秒1个单位长度的速度向左移动.设正方形和长方形重叠部分的面积为S,移动时间为t.
(1)、按方法C剪裁的有张白板纸.(用含的代数式表示)(2)、将100张白板纸裁剪完后,一共可以裁出多少个侧面与多少个底面?(用含的代数式表示,结果要化简)(3)、当时,最多可以制作该种型号的长方体纸箱多少个?25. 如图1,正方形和长方形的周长相等,且各有一条边在数轴上,点对应的数分别是 . 正方形以每秒2个单位长度的速度向右移动,同时长方形以每秒1个单位长度的速度向左移动.设正方形和长方形重叠部分的面积为S,移动时间为t.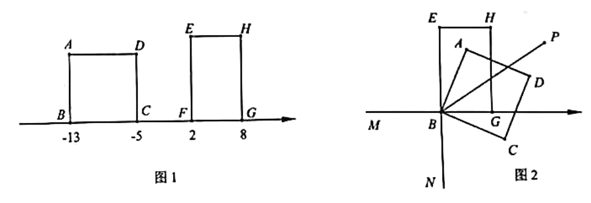 (1)、长方形的面积是 .(2)、当S是长方形面积的一半时,求t的值.(3)、如图2,当正方形和长方形运动到点B和点F重合时,停止运动,将正方形绕点B顺时针旋转,旋转角度为 , 点分别在线段、线段的延长线上,平分 , 判断和之间的数量关系,用等式表示,并说明理由.
(1)、长方形的面积是 .(2)、当S是长方形面积的一半时,求t的值.(3)、如图2,当正方形和长方形运动到点B和点F重合时,停止运动,将正方形绕点B顺时针旋转,旋转角度为 , 点分别在线段、线段的延长线上,平分 , 判断和之间的数量关系,用等式表示,并说明理由.