北京市燕山区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-02-23 类型：期末考试

进入出卷网下载

一、单选题

1. 2022的相反数是（）

A、2022 B、-2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 根据《北京市“十四五”信息通信行业发展规划》，预计到2025年末，北京市将建成并开通5G基站63000个，基本实现对城市、乡镇、行政村和主要道路的连续覆盖．将63000用科学记数法表示应为（）

A、63×10³ B、6.3×10³ C、6.3×10⁴ D、0.63×10⁵

查看试题解析
3. 已知x＝1是关于x的一元一次方程x＋2a＝0的解，则a的值是（）

A、－2 B、2 C、 $\frac{1}{2}$ D、－ $\frac{1}{2}$

查看试题解析
4. 下列各组中的两个单项式是同类项的是（）

A、－3与 $a$ B、 $2 a^{2} b$ 与 $- 3 a^{2} b$ C、 $3 a^{3}$ 与 $2 a^{2}$ D、 $a^{3} b^{2}$ 与 $\frac{1}{2} a^{2} b^{3}$

查看试题解析
5. 有理数a在数轴上的对应点的位置如图所示，若有理数b满足 $| b | < a$ ，则b的值不可能是（）

A、－3 B、－1 C、0 D、2

查看试题解析
6. 已知∠A与∠B互余，∠A＝ $56 ° 15$ ，则∠B＝（）

A、 $34 ° 45$ B、 $33 ° 45$ C、 $124 ° 45$ D、 $123 ° 45$

查看试题解析
7. 下面的框图表示解方程 $\frac{x + 1}{2} ＝ \frac{8 - x}{4}$ 的流程，其中第①步和第⑤步变形的依据相同，这两步变形的依据是（）

A、乘法分配律 B、分数的基本性质 C、等式的两边加（或减）同一个数，结果仍相等 D、等式的两边乘同一个数，或除以同一个不为0的数，结果仍相等

查看试题解析
8. 我国明朝数学家程大位所著的《算法统宗》中介绍了一种计算乘法的方法，称为“铺地锦”．例如，如图1所示，计算31×47，首先把乘数31和47分别写在方格的上面和右面，然后以31的每位数字分别乘以47的每位数字，将结果计入对应的格子中（如3×4＝12的12写在3下面的方格里，十位1写在斜线的上面，个位2写在斜线的下面），再把同一斜线上的数相加，结果写在斜线末端，最后把得数依次写下来是1457，即31×47＝1457．
如图2，用“铺地锦”的方法表示两个两位数相乘，则a的值是（）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

9. 请写出一个比－1小的有理数：．

查看试题解析
10. 燕山总工会开展“健步迎冬奥，一起向未来”职工健步走活动，职工每天健康走路6000步即为达标．某天，小王走了8105步，记为＋2105步；小李走了5700步，记为步．

查看试题解析
11. 用四舍五入法将3.594精确到0.01，所得到的近似数是．

查看试题解析
12. 下列几何体的展开图中，能围成圆锥的是．

查看试题解析
13. 如图，点C在线段AB上，点D是线段AB的中点，AB＝10cm，AC＝7cm，则CD＝cm．

查看试题解析
14. 如图，射线OC在∠AOB内部，要使OC是∠AOB的平分线，需要添加的一个条件是：．

查看试题解析
15. 图中的四边形均为长方形，请用含x的代数式表示出图中阴影部分的面积．

查看试题解析
16. 周末，小康一家和姑姑一家（共6人）相约一起去观看电影《长津湖》．小康用手机查到家附近两家影城的票价和优惠活动如下：
影城
票价（元）
优惠活动
时光影城
48
学生票半价
遇见影城
50
网络购票，总价打八折
小康利用网络给所有人都购了票，他发现在两家影城购票的总费用相同，则购票的总费用是元，两家共有学生．

查看试题解析

三、解答题

17. 计算：

(1)、|－5|＋（＋3）－（－2）；

(2)、 $- 3^{3}$ ×（ $\frac{1}{9}$ ＋ $\frac{1}{3}$ ）－（－4）÷（－2）．

查看试题解析
18. 化简：

(1)、 $5 a - 3 b - 2 a + 4 b$ ；

(2)、 $3 (2 a^{2} - a + 1) - 2 (a^{2} + 2 a) - 3$ ．

查看试题解析
19. 解方程：

(1)、 $5 x - 3 = 11 - 2 x$ ；

(2)、 $\frac{x - 1}{2} = 1 - \frac{x}{3}$ ．

查看试题解析
20. 求代数式 $\frac{1}{3} (x^{2} + 4 y) - \frac{2}{3} (3 + 2 y - x^{2}) - 2 y^{2}$ 的值，其中x＝2，y＝－1．

查看试题解析
21. 如图，已知∠MON＝60°，点A在射线OM上，点B在射线ON下方．请选择合适的画图工具按要求画图并回答问题．（要求：不写画法，保留画图痕迹）

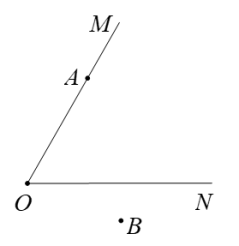(1)、过点A作直线l，使直线l只与∠MON的一边相交；

(2)、在射线ON上取一点C，使得OC＝OA，连接AC，度量∠OAC的大小为 °；（精确到度）

(3)、在射线ON上作一点P，使得AP＋BP最小，作图的依据是．

查看试题解析
22. 列一元一次方程解应用题：“共和国勋章”获得者，“杂交水稻之父”袁隆平院士一生致力于提高水稻的产量，为解决人类温饱问题做出了巨大贡献．某农业基地现有A，B两块试验田各20亩，A块种植普通水稻，B块种植杂交水稻，两块试验田单次共收获水稻33600千克．已知杂交水稻的亩产量是普通水稻亩产量的1.8倍．求杂交水稻的亩产量是多少千克？

查看试题解析
23. 如图，数轴上点A，B，M，N表示的数分别为－1，5，m，n，且AM＝ $\frac{2}{3}$ AB，点N是线段BM的中点，求m，n的值．

查看试题解析
24. 如图，点O在直线AB上，∠COD＝60°，射线OE在∠COD内部，且∠AOE＝2∠DOE．

(1)、如图1，若OD是∠BOC的平分线，求∠COE的度数；
下面是小宇同学的解答过程，请帮小宇补充完整．
解：如图1，
∵OD是∠BOC的平分线，
∴∠BOD＝∠  ▲   ＝60°，
∴∠AOD＝180°－∠BOD＝120°．
∵∠AOD＝∠AOE＋∠DOE，∠AOE＝2∠DOE，
∴∠AOD＝3∠  ▲   ，
∴∠DOE＝ $\frac{1}{3}$ ∠AOD＝40°，
∴∠COE＝∠  ▲  －∠DOE＝20°．

(2)、如图2，小宇发现当∠BOD的大小发生变化时，∠COE与∠BOD的数量关系保持不变，请你用等式表示出∠COE与∠BOD的数量关系，并说明理由．

查看试题解析
25. 我们规定：使得 $a - b = a b$ 成立的一对数a，b为“积差等数对”，记为（a，b）．例如，因为1.5－0.6＝1.5×0.6，（－2）－2＝（－2）×2，所以数对（1.5，0.6），（－2，2）都是“积差等数对”．

(1)、下列数对中，是“积差等数对”的是；
① （2， $\frac{2}{3}$ ）；② （1.5，3）；③（－ $\frac{1}{2}$ ，－1）．

(2)、若（k，－3）是“积差等数对”，求k的值；

(3)、若（m，n）是“积差等数对”，求代数式 $4 [3 m n - m - 2 (m n - 1)] - 2 (3 m^{2} - 2 n) + 6 m^{2}$ 的值．

查看试题解析

影城	票价（元）	优惠活动
时光影城	48	学生票半价
遇见影城	50	网络购票，总价打八折