上海市松江区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-02-23 类型:期末考试
一、填空题
-
1. 化简:= .2. 一元二次方程的根是 .3. 在实数范围内分解因式:2x2﹣4= .4. 函数的定义域为 .5. 若关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是 .6. 正比例函数图像经过点(1,-1),那么k= .7. 已知 , 化简= .8. 不等式的解集是 .9. 已知反比例函数的图象位于第二、四象限,则k的取值范围是 .10. 已知两个定点A、B的距离为4厘米,那么到点A、B距离之和为4厘米的点的轨迹是 .11. 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,AD=4,CD=2,那么∠A=度.
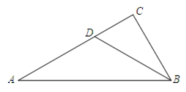 12. 如图, 垂直平分 , 垂直平分 ,若 ,则 °.
12. 如图, 垂直平分 , 垂直平分 ,若 ,则 °. 13. 在△ABC中,AD是BC边上的中线,AD⊥AB,如果AC=5,AD=2,那么AB的长是 .14. 如图,长方形ABCD中,BC=5,AB=3,点E在边BC上,将△DCE沿着DE翻折后,点C落在线段AE上的点F处,那么CE的长度是 .
13. 在△ABC中,AD是BC边上的中线,AD⊥AB,如果AC=5,AD=2,那么AB的长是 .14. 如图,长方形ABCD中,BC=5,AB=3,点E在边BC上,将△DCE沿着DE翻折后,点C落在线段AE上的点F处,那么CE的长度是 .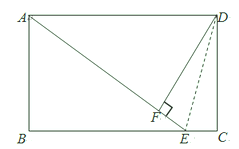
二、单选题
-
15. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、16. 已知正比例函数的图像经过点(2,4)、(1,)、(1,),那么与的大小关系是( )A、 B、 C、 D、无法确定17. 某果园今年栽种果树 棵,现计划扩大种植面积,使今后两年的栽种量都比前一年增长一个相同的百分数,这样三年(包括今年)的总栽种量为 棵.若这个百分数为 ,则由题意可列方程为( )A、 B、 C、 D、18. 下列命题中,假命题是( )A、三角形三条边的垂直平分线的交点到三角形三个顶点的距离相等 B、三角形三个内角的平分线的交点到三角形三条边的距离相等 C、两腰对应相等的两个等腰三角形全等 D、一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等
三、解答题
-
19. 计算: .20. 用配方法解方程: .21. 如图,在△ABC中,∠B=45°,∠C=30°,边AC的垂直平分线分别交边BC、AC于点D、E,DC=6.求AB的长.
 22. 小王上午8时自驾小汽车从家里出发,到“番茄农庄”游玩,小汽车离家的距离s(千米)与对应的时刻t(时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:
22. 小王上午8时自驾小汽车从家里出发,到“番茄农庄”游玩,小汽车离家的距离s(千米)与对应的时刻t(时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题: (1)、“番茄农庄”离小王家千米;(2)、小王在“番茄农庄”游玩了小时;(3)、在去“番茄农庄”的过程中,小汽车的平均速度是千米/小时;(4)、小王回到家的时刻是时分.23. 已知 , 与x成正比例,与x成反比例,且当时,;当时, .(1)、求y关于x的函数解析式;(2)、当时,求y的值.24. 如图,在四边形ABCD中,AB=AD,BC>CD,AC平分∠BCD,过点A作AE⊥BC,垂足为点E.
(1)、“番茄农庄”离小王家千米;(2)、小王在“番茄农庄”游玩了小时;(3)、在去“番茄农庄”的过程中,小汽车的平均速度是千米/小时;(4)、小王回到家的时刻是时分.23. 已知 , 与x成正比例,与x成反比例,且当时,;当时, .(1)、求y关于x的函数解析式;(2)、当时,求y的值.24. 如图,在四边形ABCD中,AB=AD,BC>CD,AC平分∠BCD,过点A作AE⊥BC,垂足为点E.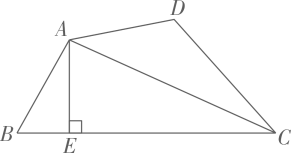 (1)、求证:CE=CD+BE;(2)、如果CE=3BE,求的值.25. 如图,在直角坐标平面内,正比例函数的图像与一个反比例函数图象在第一象限内的交点为点A,过点A作AB⊥x轴,垂足为点B,AB=3.
(1)、求证:CE=CD+BE;(2)、如果CE=3BE,求的值.25. 如图,在直角坐标平面内,正比例函数的图像与一个反比例函数图象在第一象限内的交点为点A,过点A作AB⊥x轴,垂足为点B,AB=3.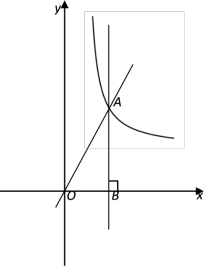 (1)、求反比例函数的解析式;(2)、在直线AB上是否存在点C,使点C到直线OA的距离等于它到点B的距离?若存在,求点C的坐标;若不存在,请说明理由;(3)、已知点P在直线AB上,如果△AOP是等腰三角形,请直接写出点P的坐标.26. 如图,在Rt△ABC中,∠ABC=90°,∠C=30°,AB=1,点D是边AC上一点(不与点 A、C重合),EF垂直平分BD,分别交边AB、BC于点E、F,联结DE、DF.
(1)、求反比例函数的解析式;(2)、在直线AB上是否存在点C,使点C到直线OA的距离等于它到点B的距离?若存在,求点C的坐标;若不存在,请说明理由;(3)、已知点P在直线AB上,如果△AOP是等腰三角形,请直接写出点P的坐标.26. 如图,在Rt△ABC中,∠ABC=90°,∠C=30°,AB=1,点D是边AC上一点(不与点 A、C重合),EF垂直平分BD,分别交边AB、BC于点E、F,联结DE、DF.

 (1)、如图1,当BD⊥AC时,求证:EF=AB;(2)、如图2,设CD=x,CF=y,求y与x的函数解析式,并写出函数的定义域;(3)、当BE=BF时,求线段CD的长.
(1)、如图1,当BD⊥AC时,求证:EF=AB;(2)、如图2,设CD=x,CF=y,求y与x的函数解析式,并写出函数的定义域;(3)、当BE=BF时,求线段CD的长.