山东省潍坊安丘市、高密市2021-2022学年八年级上学期期末考试数学试题

试卷更新日期：2022-02-23 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 $\frac{a - 1}{a} + \frac{1}{a}$ 的结果为（　　）

A、1 B、﹣1 C、 $\frac{a + 2}{a}$ D、 $\frac{a - 2}{a}$

查看试题解析
2. 如图所示，四边形ABCD是平行四边形，点E在线段BC的延长线上，若∠DCE＝128°，则∠A＝（　　）

A、32° B、42° C、52° D、62°

查看试题解析
3. 15名学生演讲赛的成绩各不相同，若某选手想知道自己能否进入前8名，则他不仅要知道自己的成绩，还应知道这15名学生成绩的（）

A、平均数 B、众数 C、方差 D、中位数

查看试题解析
4. 分式方程 $\frac{2 - x}{x - 3} - \frac{1}{3 - x} = 1$ 的解为（　　）

A、x＝2 B、无解 C、x＝3 D、x＝﹣3

查看试题解析
5. 两个直角三角板如图摆放，其中∠BAC＝∠EDF＝90°，∠F＝45°，∠B＝60°，AC与DE交于点M．若BC∥EF，则∠DMC的大小为（　　）

A、100° B、105° C、115° D、120°

查看试题解析
6. 已知两个不等于0的实数a、b满足 $a + b = 0$ ，则 $\frac{b}{a} + \frac{a}{b}$ 等于（）

A、 $- 2$ B、 $- 1$ C、1 D、2

查看试题解析
7. 如图，OA平分∠BOD，AC⊥OB于点C，且AC=2，已知点A到y轴的距离是3，那么点A关于x轴对称的点的坐标为（　　）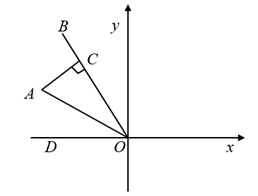

A、(2，3) B、(3，2) C、(-2，-3) D、(-3，-2)

查看试题解析
8. 为了解学生的睡眠状况，调查了一个班50名学生每天的睡眠时间，绘成睡眠时间条形统计图如图所示，则所调查学生睡眠时间的众数，中位数分别为（　　）

A、7h，7h B、8h，7.5h C、7h，7.5h D、8h，8h

查看试题解析

二、多选题

9. 下列命题是真命题的是（　　）

A、过线段中点的直线是线段的垂直平分线 B、对角线互相平分且相等的四边形是矩形 C、三角形的中位线将三角形的面积分成1：2两部分 D、对角线互相垂直的矩形是正方形

查看试题解析
10. 下列运算正确的是（　　）

A、 $\frac{2 b}{9 a} \cdot \frac{3 a}{4 b^{2}} = \frac{1}{6 b}$ B、 $(a - \frac{1}{b}) \div (\frac{1}{a} - b) = - \frac{a}{b}$ C、 $\frac{1}{2 a} + \frac{1}{a} = \frac{1}{3 a}$ D、 $\frac{1}{3 a b} \div \frac{2 b}{3 a^{2}} = \frac{a}{2 b}$

查看试题解析
11. 如图，已知在△ABC中，∠ABC＜90°，AB≠BC，BE是AC边上的中线．按下列步骤作图：①分别以点B，C为圆心，大于线段BC长度一半的长为半径作弧，相交于点M，N；②过点M，N作直线MN，分别交BC，BE于点D，O；③连接CO，DE．则下列结论正确的是（　　）

A、OB＝OC B、∠BOD＝∠COD C、DB＝DE D、AB=2DE

查看试题解析
12. 如图，四边形ABCD为菱形，BF $∥$ AC，DF交AC的延长线于点E，交BF于点F，且CE：AC＝1：2．则下列结论正确的有（）

A、△CBE≌△CDE B、DE＝FE C、AE=BE D、S_△BEF₌S_四_边_形ABCD

查看试题解析

三、填空题

13. 已知一组数据：7、a、6、5、5、7的众数为7，则这组数据的中位数是．

查看试题解析
14. 如图所示，线段BC为等腰△ABC的底边，矩形ADBE的对角线AB与DE交于点O，若OD＝2，则AC＝．

查看试题解析
15. 如图，点E是矩形ABCD边AD上一点，点F，G，H分别是BE，BC，CE的中点，AF＝6，则GH的长为．

查看试题解析
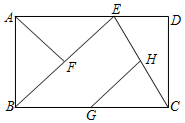16. “绿水青山就是金山银山”．某地为美化环境，计划种植树木2000棵．由于志愿者的加入，实际每天植树的棵树比原计划增加了25%，结果提前4天完成任务．则实际每天植树棵．

查看试题解析

四、解答题

17. 先化简，再求值：
$(\frac{a}{a + 2} + \frac{9 - 4 a}{a^{2} - 4}) \div \frac{a - 3}{a - 2}$ ，其中a是已知两边分别为2和3的三角形的第三边长，且a是整数．

查看试题解析
18. 作图题：

(1)、如图，已知直线l₁∥l₂ ，直线l₃分别与l₁、l₂交于点A、B．请用尺规作图法，在线段AB上求作一点P，使点P到l₁、l₂的距离相等．（保留作图痕迹，不写作法）

(2)、如图，在7×7的正方形网格中，网格线的交点称为格点，点A，B在格点上，每一个小正方形的边长为1．请以AB为边画菱形，使菱形的其余两个顶点都在格点上（画出一个即可）．并计算你所画菱形的面积．

查看试题解析
19. 列方程解应用题：
随着我国科技事业的不断发展，国产无人机大量进入快递行业．现有A，B两种型号的无人机都被用来运送快件，A型机比B型机平均每小时多运送30件，A型机运送800件所用时间与B型机运送500件所用时间相等，两种无人机平均每小时分别运送多少快件？

查看试题解析
20. 小聪、小明准备代表班级参加学校“党史知识”竞赛，班主任对这两名同学测试了6次，获得如下测试成绩折线统计图.根据图中信息，解答下列问题：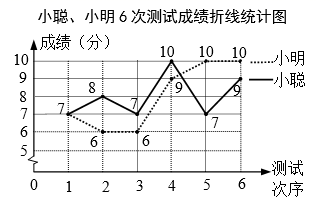

(1)、要评价每位同学成绩的平均水平，你选择什么统计量？求这个统计量.

(2)、求小聪成绩的方差.

(3)、现求得小明成绩的方差为 $S_{小明}^{2} = 3$ （单位：平方分）.根据折线统计图及上面两小题的计算，你认为哪位同学的成绩较好？请简述理由.

查看试题解析
21. 如图，在△ABC中，AB＝AC，D为BC边的中点，过点作DE⊥AB，DF⊥AC，垂足分别为E，F．

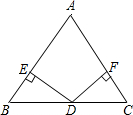(1)、求证：△BED≌△CFD；

(2)、当∠A＝90°时，试判断四边形DFAE是什么特殊四边形？并说明理由．

查看试题解析
22. 如图，在平行四边形ABCD中，对角线AC与BD相交于点O，过点O的直线EF与BA、DC的延长线分别交于点E、F．

(1)、求证：AE＝CF；

(2)、请再添加一个条件，使四边形BFDE是菱形，并说明理由．

查看试题解析
23. 问题解决：如图1，在矩形ABCD中，点E，F分别在AB，BC边上，DE＝AF，DE⊥AF于点G．

(1)、求证：四边形ABCD是正方形；

(2)、①延长CB到点H，使得BH＝AE，判断△AHF的形状，并说明理由．
②类比迁移：如图2，在菱形ABCD中，点E，F分别在AB，BC边上，DE与AF相交于点G，DE＝AF，△AED＝60°，AE＝7，BF＝2，则DE=_▲ ．（只在图2中作辅助线，并简要说明其作法，直接写出DE的长度

查看试题解析