山东省青岛市胶州市2021-2022学年八年级上学期期末数学试题
试卷更新日期：2022-02-23 类型：期末考试
一、单选题
-
1. 的相反数是（ ）A、﹣ B、 C、 D、32. 下列语句是命题的是（ ）A、垃级分类是一种生活时尚 B、今天，你微笑了吗？ C、多彩的青春 D、一起向未来3. 在平面直角坐标系中，已知点P（2a﹣4，a+3）在x轴上，则点（﹣a+2，3a﹣1）所在的象限为（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图，AB∥CD，AE平分∠BAC，若∠AEC=68°，则∠C的度数为（ ）
A、22° B、44° C、54° D、68°5. 已知一次函数y=kx+b（k，b为常数，且k≠0）的图象经过点（0，-1），且y的值随x值的增大而增大，则这个一次函数的表达式可能是（ ）A、y＝﹣2x+1 B、y＝2x+1 C、y＝﹣2x﹣1 D、y＝2x﹣16. 如图，将直角三角形纸片沿AD折叠，使点B落在AC延长线上的点E处．若AC＝3，BC=4，则图中阴影部分的面积是（ ）
A、 B、 C、 D、7. 在“传唱红色经典，弘扬爱国精神”比赛中，七位评委给某选手打出了7个原始分，余下5个有效分的平均值作为这位选手的最后得分，则7个原始分和5个有效分这两组数据相比较，一定不会发生改变的是（ ）A、方差 B、极差 C、中位数 D、平均数8. 已知一次函数y＝k1x+b1和一次函数y1＝k2x+b2的自变量x与因变量y1 ， y2的部分对应数值如表所示，则关于x、y的二元一次方程组的解为（ ）x
…
﹣2
﹣1
0
1
2
…
y1
…
﹣1
0
1
2
3
…
y2
…
﹣5
﹣3
﹣1
1
3
…
A、 B、 C、 D、二、填空题
-
9. 若是某个二元一次方程的一个解，则该方程可能是 （请写出满足条件的一个答案即可）10. 如图，每个小正方形的边长为2，剪一剪，拼成一个正方形，则这个正方形的边长是 ．
11. 某校团委对该校八年级三个班级的“创文明校园，做文明学生”情况进行了检查，三个班级的各项成绩（单位：分）如表所示，如果将自习纪律，教室卫生，仪容仪表这三项得分依次按30%，30%，40%的比例计算各班的成绩，则二班的最终成绩是 分．自习纪律
教室卫生
仪容仪表
一班
90
98
95
二班
96
90
98
三班
98
97
90
12. 如图，将边长为4的正方形放在平面直角坐标系中，若点A的坐标是（-1，2），则点C的坐标是 ．
13. 为了解班级同学在假期参加志愿者服务活动情况，小明随机调查了班级20名同学参加活动的时间，结果如图所示，则这组数据的众数是小时．
14. 如图，在△ABC中，D，E分别是边AB和BC上的点，若∠B＝35°，∠C＝56°．∠F＝47°，则∠ADF的度数为 ．
15. 如图，AB=4，点M为线段AB上的一个动点，在AB同侧分别以AM和BM为边作等边△AMC和等边△BMD，则线段CD的最小值为 ．
16. 在平面直角坐标系中，若点P的坐标为（x，y），点Q的坐标为（mx+y，x+my），则称点Q是点P的m级派生点，例如点P（1，2）（3×1+2，1+3×2），即Q（5，7）．如图点Q（﹣5，4）是点P（x，y）的﹣级派生点，点A在x轴上，且S△APQ＝4，则点A的坐标为 ．
三、解答题
-
17.(1)、计算：(2)、计算：（﹣）+(3)、解方程组：(4)、解方程组：18. 已知：如图．在△ABC中．点D，E，F分到在边AB，AC，BC上，CD与EF相交于点H，且∠BDC+∠DHF＝180°．∠DEF=∠B，求证：DE∥BC．
19. “冰雪之约，中国之邀”，第24届冬季奥林匹克运动会即将在中国举行．某国家队计划从甲、乙两名短道速滑运动员中选派一人参赛（均取整数，单位：秒）如下：甲：37，41，38，40，39，37，39，42，37，40
乙：36，39，37，38，42，39，39，41，42，37
【整理数据】
甲成绩的扇形统计图（图1）：
乙成绩的频数分布直方图（图2）：
【分析数据】
运动员
平均数
中位数
众数
方差
甲
39
a
37
c
乙
39
39
b
4
请根据以上信息，完成下列问题：
(1)、甲成绩的中位数a落在扇形统计图的 部分（填A，B，C）；(2)、请补全乙成绩的频数分布直方图；(3)、表中b＝ ， c＝；(4)、【做出决策】根据甲、乙两人10次选拔比赛的成绩，你认为该国家队应选派哪位运动员参赛？并说明理由．
20. 如图，在四边形ABCD中，AB∥CD，∠ADC=90°，E在AC上．EC＝ED＝DA．求∠CAB的度数．
21. 某种植户准备将一批农产品运往外地销售，计划同时租用运输公司的A，B两种型号的货车，租车费用分别是380元/辆，180元/辆，已知A，B两种型号货车的运载能力如图所示．该种植户计划一次性运完21吨农产品，且每辆车都恰好载满货物，请你帮助他设计一种最省钱的租车方案．
22. A，B两地相距560km，甲车从A地驶往B地，1h后，乙车以相同的速度沿同一条路线从B地驶往A地，乙车行驶1小时后，乙车的速度提高到120km/h，并保持此速度直到A地．在整个行驶过程中，甲车到A地的距离y1（km），乙车到A地的距离y2（km）与甲车行驶的时间x（h）之间的关系如图所示，根据图象回答下列问题：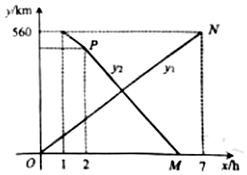
(1)、图中点P的坐标是 ， 点M的坐标是 ．(2)、甲、乙两车之间的距离不超过240km的时长是多少？23. 【问题提出】能否把一个正方形分割成2022个小正方形？（小正方形大小可以不同，但不能重叠）
【问题探究】
为了解决问题，我们采取一般问题特殊化的策略，先从最简单的情形入手，从中找出解决问题的方法，最后得出一般性的结论．
探究一；
如图1①，把正方形的四条边2等分（把每条边分成相等的2份）．然后连接相对边的2等分点就可以把正方形分割成4=22个小正方形．
探究二：
如图1②，把正方形的四条边3等分（把每条边分成相等的3份），然后连接相对边的3等分点就可以把正方形分制成9＝32个小正方形．
如果再把图1②中相邻的4个小正方形进行拼合，如图1③所示，则可以把一个正方形分割成6个小正方形．
探究三：
(1)、把正方形的四条边4等分（把每条边分成相等的4份），然后连接相对边的4等分点就可以把正方形分割成个小正方形，如果再把相邻的9个小正方形进行拼合，则可以把一个正方形分割成 个小正方形．(2)、 【归纳结论】根据以上探究思路，把一个正方形的四条边n等分，然后连接相对边的n等分点就可以把正方形分割成个小正方形、如果再把相邻的（n﹣1）2个小正方形进行拼合，则可以把一个正方形分割成 个小正方形．(3)、 【问题解决】把一个正方形的四条边等分，然后连接相对边的等分点就可以把正方形分割成个小正方形，如果把相邻的个小正方形进行拼合，则可以把一个正方形分割成2022个小正方形．(4)、 【拓展应用】把一个立方块控如图2所示的方式进行分割，则共分割成 个小立方块．24. 在四边形ABCD中，AB∥CD，∠BCD=90°，AB=8cm，BC=6cm，AD=10cm，以CD所在直线为x轴，以经过点A并且与CD垂直的直线为y轴，建立平面直角坐标系（如图）．点P，Q分别是线段AB和CD上的动点，点P以1cm/s的速度从点B向点A运动，同时点Q以2cm/s的速度从点D向点C运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为t（s）（0＜t＜8），请回答下列问题：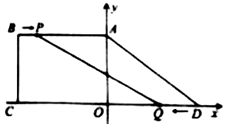
(1)、用含t的代数式表示点P的坐标；(2)、设四边形PBCQ的面积为S cm2 ， 求S与t之间的关系式．(3)、在运动过程中，是否存在某一时刻t，使四边形PBCQ的面积恰为四边形ABCD面积的？若存在，求出t的值；若不存在，请说明理由；(4)、连接BQ，求t为何值时，直线BQ与y轴的交点坐标为（0，-2）？