江西省赣州市章贡区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-02-23 类型:期末考试
一、单选题
-
1. 冬季奥林匹克运动会是世界规模最大的冬季综合性运动会,下列四个图分别是第24届冬奥会图标中的一部分,其中是轴对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算,正确的是( )A、a2•a=a2 B、a+a=a2 C、a6÷a3=a2 D、(a3)2=a63. 如果x2+mx+9是一个完全平方式,则m的值为( )A、3 B、6 C、±3 D、±64. 将分式中的x,y的值同时扩大为原来的3倍,则分式的值( )A、扩大6倍 B、扩大9倍 C、不变 D、扩大3倍5. 如图的4×4的正方形网格中,有A、B两点,在直线a上求一点P,使PA+PB最短,则点P应选在( )
2. 下列运算,正确的是( )A、a2•a=a2 B、a+a=a2 C、a6÷a3=a2 D、(a3)2=a63. 如果x2+mx+9是一个完全平方式,则m的值为( )A、3 B、6 C、±3 D、±64. 将分式中的x,y的值同时扩大为原来的3倍,则分式的值( )A、扩大6倍 B、扩大9倍 C、不变 D、扩大3倍5. 如图的4×4的正方形网格中,有A、B两点,在直线a上求一点P,使PA+PB最短,则点P应选在( ) A、C点 B、D点 C、E点 D、F点6. 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动(不与端点重合),且保持AD=CE,连接DE、DF、EF,在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE的面积是12;③AD+BE>DE.其中正确的结论是( ).
A、C点 B、D点 C、E点 D、F点6. 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动(不与端点重合),且保持AD=CE,连接DE、DF、EF,在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE的面积是12;③AD+BE>DE.其中正确的结论是( ). A、①② B、①③ C、①②③ D、②③
A、①② B、①③ C、①②③ D、②③二、填空题
-
7. 某种秋冬流感病毒的直径约为米,该直径用科学记数法表示为 .8. 若分式 的值为0,则x的值为.9. 如图, , ,要使 ,应添加的条件是 . (只需写出一个条件即可)
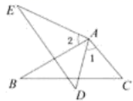 10. 因式分解: .11. 如图,∠BAC=100°,若MP和NQ分别垂直平分AB和AC,则∠PAQ= .
10. 因式分解: .11. 如图,∠BAC=100°,若MP和NQ分别垂直平分AB和AC,则∠PAQ= .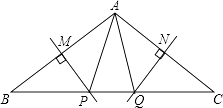 12. 如图, 是等边三角形,点 是 边的中点,点 在直线 上,若 是轴对称图形,则 的度数为
12. 如图, 是等边三角形,点 是 边的中点,点 在直线 上,若 是轴对称图形,则 的度数为
三、解答题
-
13.(1)、解方程:(2)、已知等腰三角形的两边长为5cm和4cm,求它的周长.14. 化简求值: ,其中 , .15. 已知 和 都为正三角形,点B,C,D在同一直线上,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.
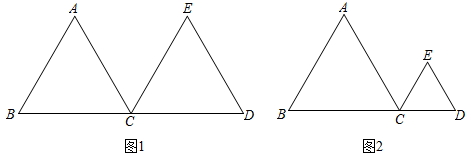 (1)、如图1,当 时,作 的中线 ;(2)、如图2,当 时,作 的中线 .16. 如图,点A、B、C、D在一条直线上,EA//FB,EC//FD,EA=FB.求证:AB=CD.
(1)、如图1,当 时,作 的中线 ;(2)、如图2,当 时,作 的中线 .16. 如图,点A、B、C、D在一条直线上,EA//FB,EC//FD,EA=FB.求证:AB=CD. 17. 化简分式 , 并从1、2、3这三个数中取一个合适的数作为x的值代入求值.18. 如图所示,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.
17. 化简分式 , 并从1、2、3这三个数中取一个合适的数作为x的值代入求值.18. 如图所示,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F. (1)、求证:△ABE≌△CAD;(2)、若BP⊥AD于点P,PF=6,求BF的长.19. 接种疫苗是阻断新冠病毒传播的有效途径,针对疫苗急需问题,某制药厂紧急批量生产,计划每天生产疫苗16万剂,但受某些因素影响,有10名工人不能按时到厂.为了应对疫情,回厂的工人加班生产,由原来每天工作8小时增加到10小时,每人每小时完成的工作量不变,这样每天只能生产疫苗15万剂.(1)、求该厂当前参加生产的工人有多少人?(2)、生产4天后,未到的工人同时到岗加入生产,每天生产时间仍为10小时.若上级分配给该厂共760万剂的生产任务,问该厂共需要多少天才能完成任务?20. 如图,在四边形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
(1)、求证:△ABE≌△CAD;(2)、若BP⊥AD于点P,PF=6,求BF的长.19. 接种疫苗是阻断新冠病毒传播的有效途径,针对疫苗急需问题,某制药厂紧急批量生产,计划每天生产疫苗16万剂,但受某些因素影响,有10名工人不能按时到厂.为了应对疫情,回厂的工人加班生产,由原来每天工作8小时增加到10小时,每人每小时完成的工作量不变,这样每天只能生产疫苗15万剂.(1)、求该厂当前参加生产的工人有多少人?(2)、生产4天后,未到的工人同时到岗加入生产,每天生产时间仍为10小时.若上级分配给该厂共760万剂的生产任务,问该厂共需要多少天才能完成任务?20. 如图,在四边形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC. (1)、如图1,若α=90°,根据教材中一个重要性质直接可得DA=CD,这个性质是;(2)、如图2,求证AD=CD.21. 图1是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)、如图1,若α=90°,根据教材中一个重要性质直接可得DA=CD,这个性质是;(2)、如图2,求证AD=CD.21. 图1是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形. (1)、观察图2,请你写出下列三个代数式(a+b)2 , (a﹣b)2 , ab之间的等量关系为 .(2)、运用你所得到的公式,计算:若m、n为实数,且mn=﹣3,m﹣n=4,试求m+n的值.(3)、如图3,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=26,求图中阴影部分面积.22. 【阅读材料】小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则ABD≌ACE.
(1)、观察图2,请你写出下列三个代数式(a+b)2 , (a﹣b)2 , ab之间的等量关系为 .(2)、运用你所得到的公式,计算:若m、n为实数,且mn=﹣3,m﹣n=4,试求m+n的值.(3)、如图3,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=26,求图中阴影部分面积.22. 【阅读材料】小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则ABD≌ACE. (1)、【材料理解】在图1中证明小明的发现.(2)、【深入探究】如图2,ABC和AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°,其中正确的有 . (将所有正确的序号填在横线上)(3)、【延伸应用】如图3,在四边形ABCD中,BD=CD,AB=BE,∠ABE=∠BDC=60°,试探究∠A与∠BED的数量关系,并证明.23. 如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D—A返回到点A停止,点P的运动时间为t秒.
(1)、【材料理解】在图1中证明小明的发现.(2)、【深入探究】如图2,ABC和AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°,其中正确的有 . (将所有正确的序号填在横线上)(3)、【延伸应用】如图3,在四边形ABCD中,BD=CD,AB=BE,∠ABE=∠BDC=60°,试探究∠A与∠BED的数量关系,并证明.23. 如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D—A返回到点A停止,点P的运动时间为t秒. (1)、当t=3秒时,BP=cm;(2)、当t为何值时,连结CP,DP,△CDP为等腰三角形;(3)、Q为AD边上的点,且DQ=5,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与△DCQ全等.
(1)、当t=3秒时,BP=cm;(2)、当t为何值时,连结CP,DP,△CDP为等腰三角形;(3)、Q为AD边上的点,且DQ=5,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与△DCQ全等.