吉林省长春市二道区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-02-23 类型:期末考试
一、单选题
-
1. 16的平方根为( )A、4 B、-4 C、 D、2. 下列四个实数中无理数是( )A、0 B、 C、 D、3. 计算a2•(﹣a2)3的结果是( )A、a7 B、a8 C、﹣a8 D、﹣a74. 下列语句中,为真命题的是( )A、过直线外一点有且只有一条直线与已知直线平行 B、有理数与数轴上的点一一对应 C、三角形的一个外角大于任何一个内角 D、两边和其中一边的对角相等的两个三角形全等5. 如图是一所学校对学生上学方式进行调查后,根据调查结果绘制了一个不完整的统计图,其中“其他”部分所对的圆心角度数是36°则步行部分所占的百分比是( )
 A、36% B、40% C、45% D、50%6. 如图,点A、D、C、F在同一条直线上,若AB=DE , BC=EF , 则下列条件中能满足△ABC≌△DEF的是( )
A、36% B、40% C、45% D、50%6. 如图,点A、D、C、F在同一条直线上,若AB=DE , BC=EF , 则下列条件中能满足△ABC≌△DEF的是( ) A、∠A=∠EDF B、AD=CF C、∠BCA=∠F D、BC EF7. 在△ABC中,∠ACB=90°,AC<BC.用无刻度的直尺和圆规在△ABC内部作一个角∠α,下列作法中∠α不等于45°的是( )A、
A、∠A=∠EDF B、AD=CF C、∠BCA=∠F D、BC EF7. 在△ABC中,∠ACB=90°,AC<BC.用无刻度的直尺和圆规在△ABC内部作一个角∠α,下列作法中∠α不等于45°的是( )A、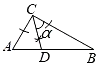 B、
B、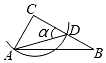 C、
C、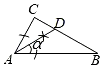 D、
D、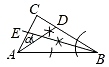 8. 如图,在∠ECF的边CE上有两点A、B,边CF上有一点D,其中BC=BD=DA且∠ECF=27°,则∠ADF的度数为( )
8. 如图,在∠ECF的边CE上有两点A、B,边CF上有一点D,其中BC=BD=DA且∠ECF=27°,则∠ADF的度数为( ) A、54° B、91° C、81° D、101°
A、54° B、91° C、81° D、101°二、填空题
-
9. 比较大小:﹣3 .10. 因式分解:x2﹣2x= .11. 若关于x的多项式(x+m)(2x﹣3)展开后不含x项,则m的值为 .12. 如图,A,B两点分别位于一个假山的两端,小明想用绳子测量A、B间的距离,首先在地面上取一个可以直接到达A点和B点的点C,连接AC并延长到点D,使CD=AC,连接BC并延长到点E,使CE=CB,连接DE并测量出它的长度为8m,则AB间的距离为 .
 13. 如图,已知的周长为13,根据图中尺规作图的痕迹,若 , 则的周长为.
13. 如图,已知的周长为13,根据图中尺规作图的痕迹,若 , 则的周长为.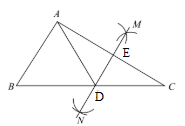 14. 如图,有5个形状大小完全相同的小长方形构造成一个大长方形(各小长方形之间不重叠且不留空隙),图中阴影部分的面积为32,则每个小长方形的对角线为 .
14. 如图,有5个形状大小完全相同的小长方形构造成一个大长方形(各小长方形之间不重叠且不留空隙),图中阴影部分的面积为32,则每个小长方形的对角线为 .
三、解答题
-
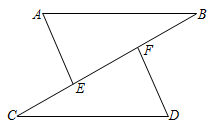
15. 计算: .16. 已知2m=3,2n=5.(1)、求2m+n的值;(2)、求22m-n的值.17. 先化简.再求值:(2x﹣y)2﹣2x(x﹣2y),其中x= , y=1.18. 如图,在△ABE和△CDF中,点C、E、F、B在同一直线上,BF=CE,若AB∥CD,∠A=∠D.求证:AB=CD.
 19. 图①、图②、图③均为3×5的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,按下列要求作图:
19. 图①、图②、图③均为3×5的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,按下列要求作图: (1)、在图①中,连结AC、BC,使AC=AB,∠BAC=90°;(2)、在图②中,连结AC、BC,使AC=BC,∠ACB=90°;(3)、在图③中,连结AC、BC,使AC=BC,∠ACB≠90°20. 为了了解长春市冬季的天气变化情况,热爱气象观察的小明记录了2021年11月份30天的天气情况,具体信息如下:
(1)、在图①中,连结AC、BC,使AC=AB,∠BAC=90°;(2)、在图②中,连结AC、BC,使AC=BC,∠ACB=90°;(3)、在图③中,连结AC、BC,使AC=BC,∠ACB≠90°20. 为了了解长春市冬季的天气变化情况,热爱气象观察的小明记录了2021年11月份30天的天气情况,具体信息如下:
日期
最高气温
最低气温
天气
日期
最高气温
最低气温
天气
11﹣01
4℃
0℃
多云
11﹣16
2℃
﹣2℃
晴
11﹣02
9℃
3℃
阴
11﹣17
6℃
﹣1℃
阴
11﹣03
12℃
2℃
晴
11﹣18
4℃
﹣6℃
多云
11﹣04
15℃
﹣2℃
阴
11﹣19
0℃
﹣6℃
多云
11﹣05
15℃
10℃
多云
11﹣20
0℃
﹣7℃
多云
11﹣06
2℃
﹣6℃
多云
11﹣21
﹣4℃
﹣9℃
阴
11﹣07
﹣3℃
﹣4℃
多云
11﹣22
﹣8℃
﹣12℃
多云
11﹣08
9℃
﹣4℃
多云
11﹣23
﹣8℃
﹣15℃
晴
11﹣09
﹣3℃
﹣6℃
多云
11﹣24
﹣7℃
﹣14℃
晴
11﹣10
﹣2℃
﹣5℃
小雪
11﹣25
﹣5℃
﹣13℃
多云
11﹣11
6℃
2℃
多云
11﹣26
﹣3℃
﹣13℃
多云
11﹣12
﹣1℃
﹣7℃
晴
11﹣27
0℃
﹣1℃
多云
11﹣13
4℃
﹣6℃
多云
11﹣28
6℃
﹣4℃
多云
11﹣14
12℃
9℃
阴
11﹣29
﹣2℃
﹣7℃
多云
11﹣15
2℃
﹣4℃
晴
11﹣30
﹣4℃
﹣11℃
多云
请你帮助小明同学把以上数据整理成统计图表.
2021年11月份长春市最低气温统计表
最低气温分组
频数
频率
10℃及10℃以上
大于等于5℃小于10℃
大于等于0℃小于5℃
4
大于等于﹣5℃小于0℃
9
0.3
大于等于﹣10℃小于﹣5℃
a
﹣10℃以下
b
m
(1)、补全条形统计图;(2)、2021年11月份长春市最低气温统计表中a=;b=;m= .21. 如图,已知线段BC是圆柱底面的直径,圆柱底面的周长为10,在圆柱的侧面上,过点A、C两点嵌有一圈长度最短的金属丝. (1)、现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是 ;(2)、求该金属丝的长.22. 例如:若a+b=3,ab=1,求a2+b2的值.
(1)、现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是 ;(2)、求该金属丝的长.22. 例如:若a+b=3,ab=1,求a2+b2的值.解:因为a+b=3,所以(a+b)2=9,即:a2+2ab+b2=9,
又因为ab=1,所以a2+b2=7.
根据上面的解题思路与方法,解决下列问题:
(1)、若x+y=8,x2+y2=40,求xy的值;(2)、填空:若(4﹣x)x=5,则(4﹣x)2+x2=;(3)、如图所示,已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,CF=2,长方形EMFD的面积是12,则x的值为 . 23. 如图:
23. 如图: (1)、感知:如图①,△ABC和△AED都是等腰直角三角形,∠BAC=∠DAE=90°,点B在线段AD上,点C在线段AE上,我们很容易得到BD=CE,不需要证明;
(1)、感知:如图①,△ABC和△AED都是等腰直角三角形,∠BAC=∠DAE=90°,点B在线段AD上,点C在线段AE上,我们很容易得到BD=CE,不需要证明;探究:如图②,将△AED绕点A逆时针旋转α(0<α<90°),连结BD和CE,此时BD=CE是否依然成立?若成立,写出证明过程;若不成立,说明理由;
(2)、应用:如图③,当△ADE绕点A逆时针旋转,使得点D落在BC的延长线上,连接CE;①∠ACE的度数为度;
②线段BC、CD、CE之间的数量关系是;
③若AB=AC= , CD=1,则线段DE的长为 .
24. 如图,在△ABC中,∠C=90°,AC=12,BC=5,BD平分∠ABC.动点P从点B出发,沿折线BA-AC以每秒1个单位长度的速度向点C运动,当点P不与点D重合时,连结P、B、D三点.设点P的运动时间为t秒. (1)、线段AB的长为;(2)、当DP⊥AB时,t=;(3)、求线段BD的长;(4)、当∠DBP与∠DPB相等时,直接写出t的值.
(1)、线段AB的长为;(2)、当DP⊥AB时,t=;(3)、求线段BD的长;(4)、当∠DBP与∠DPB相等时,直接写出t的值.