黑龙江省齐齐哈尔市甘南县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-02-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列长度的三条线段能组成三角形的是（）

A、3，3，4 B、7，4，2 C、3，4，8 D、2，3，5

查看试题解析
2. 改革开放以来，我国众多科技实体在各自行业取得了举世瞩目的成就，大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表．上述四个企业的标志是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 ${(- 1)}^{- 1} = 1$ B、 ${(x + 2)}^{2} = x^{2} + 4$ C、 ${(a^{})}^{2} = a^{2} b^{5}$ D、 $4 a^{3} b ÷ (- 2 a^{2} b) = - 2 a$

查看试题解析
4. 已知正n边形的一个内角为135°，则边数n的值是（　　）

A、6 B、7 C、8 D、10

查看试题解析
5. 如果把分式 $\frac{x + y}{x y}$ 中的x、y同时扩大为原来的2倍，那么该分式的值（　　）

A、不变 B、扩大为原来的2倍 C、缩小为原来的 $\frac{1}{2}$ D、缩小为原来的 $\frac{1}{4}$

查看试题解析
6. 已知点P（a ， 3）、Q（﹣2，b）关于y轴对称，则 $\frac{a + b}{a - b}$ 的值是（）

A、 $- \frac{1}{5}$ B、 $\frac{1}{5}$ C、﹣5 D、5

查看试题解析
7. 若 $x^{2} + 2 (m - 1) x + 16$ 是完全平方式，则m的值为（）

A、±8 B、 $- 3$ 或 $5$ C、 $- 3$ D、 $5$

查看试题解析
8. 如图，在△ABC中，∠BAC＝90°，AB=AC，AD是经过A点的一条直线，且B、C在AD的两侧，BD⊥AD于D，CE⊥AD于E，交AB于点F，CE=10，BD＝4，则DE的长为（　　）

A、6 B、5 C、4 D、8

查看试题解析
9. 如图，点P是∠BAC的平分线上一点，PB⊥AB于B，且PB=5cm，AC=12，则△APC的面积是（）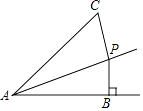

A、30cm² B、40cm² C、50cm² D、60cm²

查看试题解析
10. 如图，在△ABC中，直线l垂直平分AB分别交CB、AB于点D，E，AC＝3，CB＝4．则△ACF周长的最小值是（　　）

A、4 B、6 C、7 D、10

查看试题解析

二、填空题

11. 在人体血液中，红细胞直径约为 $0.00077 c m$ ，数据0.00077用科学记数法表示为．

查看试题解析
12. 如图，已知△ABC中，AB＝AC，要使△ABD≌ACE，则只需添加一个适当的条件是．（只填一个即可）

查看试题解析
13. 如果分式 $\frac{2}{x - 1} + (x + 3)^{0}$ 有意义，那么x的取值范围是．

查看试题解析
14. 如图，已知∠BAC＝60°，在∠BAC的平分线上截取AD＝6cm，过点D作DF⊥AB于点F，在AC上有一点E，若 $S_{Δ A E D} = \frac{15}{2} c m^{2}$ ，则AE的长为．

查看试题解析
15. 若关于x的分式方程 $\frac{x}{x - 1} = \frac{3a}{2 x - 2} - 2$ 有非负数解，则a的取值范围是.

查看试题解析
16. 已知等腰△ABC，AB＝AC，∠ABC＝20°，P为直线 $B C$ 上一点，BP＝AB，则∠PAC的度数为．

查看试题解析
17. 如图，在直角坐标系xOy中，边长为1的正方形A₁B₁C₁D₁（称为第1个正方形）的顶点A₁在原点处，点B₁在y轴上，点D₁在x轴上，点C₁在第一象限内，现以点C₁为顶点做等边三角形C₁A₂B₂ ，使得点A₂落在x轴上，且A₂B₂⊥x轴；以A₂B₂为边做正方形A₂B₂C₂D₂（称为第2个正方形），且正方形的边A₂D₂落在x轴上…如此类推，则第2020个正方形的边长为．

查看试题解析

三、解答题

18.

(1)、计算： $(- \frac{1}{2})^{- 2} + \sqrt{16} - (π - 3.14)^{0} + | - \frac{1}{2} |$ ；

(2)、因式分解： $3 a^{2} - 48$ ．

查看试题解析
19. 解方程 $\frac{1}{x + 3} - \frac{2}{3 - x} = \frac{12}{x^{2} - 9}$

查看试题解析
20. 如图，在平面直角坐标系xOy中，A（1，2），B（3，1），C（﹣2，﹣1）．

(1)、在图中作出△ABC关于y轴的对称图形△A₁B₁C₁ ．

(2)、写出点A₁ ， B₁ ， C₁的坐标（直接写答案）
A₁ B₁ C₁

(3)、求△ABC的面积．

查看试题解析
21. 如图，在△ABC中，D是边BC上的一点，AB=DB，BE平分∠ABC，交边AC于点E，连接DE．

(1)、求证：△ABE≌△DBE；

(2)、若∠A=100°，∠C=50°，求∠AEB的度数．

查看试题解析
22. 列方程解应用题：
为了提升阅读速度，某中学开设了“高效阅读”课．小敏经过一段时间的训练，发现自己现在每分钟阅读的字数比原来的2倍还多300字，现在读9100字的文章与原来读3500字的文章所用的时间相同．求小敏原来每分钟阅读的字数．

查看试题解析
23. 综合与实践

(1)、问题发现

如图1，已知△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE，求∠AEB的度数及线段AD，BE之间的数量关系；

(2)、类比探究
如图2，若△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE，

填空：①∠AEB的度数为；

②线段CM，AE，BE之间的数量关系为．

(3)、拓展延伸
在（2）的条件下，若BE=4，CM=3，则四边形ABEC的面积为．

查看试题解析
24. 如图，在平面角坐标系中，点B在y轴的负半轴上（0，﹣2 $\sqrt{3}$ ），过原点的直线OC与直线AB交于C，∠COA＝∠OCA＝∠OBA＝30°

(1)、点C坐标为， OC＝， △BOC的面积为， $\frac{S_{Δ O A C}}{S_{Δ O A B}}$ ＝；

(2)、点C关于x轴的对称点C′的坐标为；

(3)、过O点作OE⊥OC交AB于E点，则△OAE的形状为　　，请说明理由；

(4)、在坐标平面内是否存在点F使△AOF和△AOB全等，若存在，请直接写出F坐标，请说明理由．

查看试题解析