黑龙江省牡丹江市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-02-23 类型:期末考试
一、单选题
-
1. 下列图形中,是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 下列计算正确的是( )A、(﹣m3n)2=m5n2 B、6a2b3c÷2ab3=3a C、3x2÷(3x﹣1)=x﹣3x2 D、(p2﹣4p)p﹣1=p﹣43. 下列各式从左到右的变形,正确的是( )A、=﹣1 B、 C、 D、4. 如图所示,△ABC与△ADE顶点A重合,点D,E分别在边BC,AC上,且AB=AC,AD=DE,∠B=∠ADE=40°,则∠EDC的度数为( )
A、1个 B、2个 C、3个 D、4个2. 下列计算正确的是( )A、(﹣m3n)2=m5n2 B、6a2b3c÷2ab3=3a C、3x2÷(3x﹣1)=x﹣3x2 D、(p2﹣4p)p﹣1=p﹣43. 下列各式从左到右的变形,正确的是( )A、=﹣1 B、 C、 D、4. 如图所示,△ABC与△ADE顶点A重合,点D,E分别在边BC,AC上,且AB=AC,AD=DE,∠B=∠ADE=40°,则∠EDC的度数为( )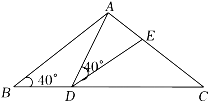 A、20° B、30° C、40° D、505. 已知x2+kxy+16y2是一个完全平方式,则k的值是( )A、4 B、±4 C、8 D、±86. 如图所示,在平面直角坐标系xOy中,△ABC关于直线y=1对称,已知点A的坐标是(3,4),则点B的坐标是( )
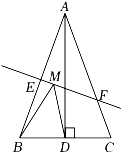
A、20° B、30° C、40° D、505. 已知x2+kxy+16y2是一个完全平方式,则k的值是( )A、4 B、±4 C、8 D、±86. 如图所示,在平面直角坐标系xOy中,△ABC关于直线y=1对称,已知点A的坐标是(3,4),则点B的坐标是( )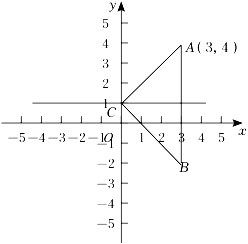 A、(3,﹣4) B、(﹣3,2) C、(3,﹣2) D、(﹣2,4)7. 若(﹣2x+a)(x﹣1)的结果中不含x的一次项,则a的值为( )A、1 B、﹣1 C、2 D、﹣28. 已知为任意实数,则多项式的值为( )A、一定为负数 B、不可能为正数 C、一定为正数 D、正数或负数或零9. 甲、乙两地相距500km,提速前动车的速度为vkm/h,提速后动车的速度是提速前的1.5倍,提速后行车时间比提速前减少10min,则可列方程为( )A、 B、 C、 D、10. 已知关于x的分式方程=2的解是负数,则n的取值范围为( )A、n>1且n≠ B、n>1 C、n<2且n≠ D、n<211. 如图所示,已知在等边三角形ABC中,点D,E分别是BC,AC上的点,且AE=CD,连接AD,BE交于点P,过点B作BQ⊥AD,Q为垂足,PQ=2,则BP的长为( )
A、(3,﹣4) B、(﹣3,2) C、(3,﹣2) D、(﹣2,4)7. 若(﹣2x+a)(x﹣1)的结果中不含x的一次项,则a的值为( )A、1 B、﹣1 C、2 D、﹣28. 已知为任意实数,则多项式的值为( )A、一定为负数 B、不可能为正数 C、一定为正数 D、正数或负数或零9. 甲、乙两地相距500km,提速前动车的速度为vkm/h,提速后动车的速度是提速前的1.5倍,提速后行车时间比提速前减少10min,则可列方程为( )A、 B、 C、 D、10. 已知关于x的分式方程=2的解是负数,则n的取值范围为( )A、n>1且n≠ B、n>1 C、n<2且n≠ D、n<211. 如图所示,已知在等边三角形ABC中,点D,E分别是BC,AC上的点,且AE=CD,连接AD,BE交于点P,过点B作BQ⊥AD,Q为垂足,PQ=2,则BP的长为( ) A、3 B、4 C、5 D、612. 如图所示,在等边三角形ABC中,D为AC边的中点,E为边BC延长线上一点,BD=DE,DF⊥BE垂足为点F.下列结论:①AD=CE;②CE+CD=AB;③∠BDE=120°;④CF:BF=1:3;⑤S△CDE=S△ABE.其中正确的有( )
A、3 B、4 C、5 D、612. 如图所示,在等边三角形ABC中,D为AC边的中点,E为边BC延长线上一点,BD=DE,DF⊥BE垂足为点F.下列结论:①AD=CE;②CE+CD=AB;③∠BDE=120°;④CF:BF=1:3;⑤S△CDE=S△ABE.其中正确的有( )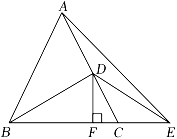 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
13. 医用外科口罩的熔喷布厚度为0.000156米,将0.000156用科学记数法表示为 .14. 当x=时,分式 的值为0.15. 观察下列分式,探究其规律: , , , , ……,按照上述规律,第n个分式是 .16. 在△ABC中,AB=AC,将△ABC折叠,使A,B两点重合,折痕所在直线与AC边所在直线的夹角为50°,则∠A的度数为 .17. 若a,b都是有理数,且满足a2+b2+5=4a﹣2b,则(a+b)2021= .18. 若25m×2×10n=57×24 , 则mn= .19. AD为等腰△ABC底边BC上的高,且AD=8,腰AB的垂直平分线EF交AC于F,M为线段EF上一动点,则BM+DM的最小值为 .
 20. 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是 (用a、b的代数式表示).
20. 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是 (用a、b的代数式表示).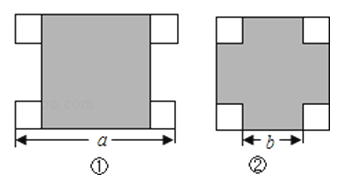
三、解答题
-
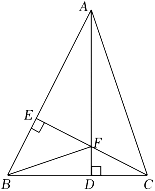
21.(1)、计算:×(﹣0.5)﹣2+20210;(2)、计算:(a+5)(a﹣3)﹣(a+1)2;(3)、因式分解:(x﹣y)2﹣x+y;(4)、解方程:=1+ .22. 先化简,再求值:÷(2x﹣),其中x=2.23. 如图,在△ABC中,边BC,AB上的高AD,CE相交于点F,且∠ACE=45°,连接BF,求∠BFE的度数.
 24. 已知∠MBN=60°,等边△BEF与∠MBN顶点B重合,将等边△BEF绕顶点B顺时针旋转,边EF所在直线与∠MBN的BN边相交于点C,并在BM边上截取AB=BC,连接AE.
24. 已知∠MBN=60°,等边△BEF与∠MBN顶点B重合,将等边△BEF绕顶点B顺时针旋转,边EF所在直线与∠MBN的BN边相交于点C,并在BM边上截取AB=BC,连接AE. (1)、将等边△BEF旋转至如图①所示位置时,求证:CE=BE+AE;(2)、将等边△BEF顺时针旋转至如图②、图③位置时,请分别直接写出AE,BE,CE之间的数量关系,不需要证明;(3)、在(1)和(2)的条件下,若BF=4,AE=1,则CE= .25. 为了更安全地开展冰上运动某校决定购进一批护肘及护膝.已知用900元购进护膝的数量比用400元购进护肘的数量多10副,且每副护膝价格是每副护肘价格的1.5倍.(1)、每副护肘和护膝的价格分别是多少元;(2)、若学校决定用不超过8000元购进两种护具共300副,且护肘数量不多于102副,求有哪几种购买方案;(3)、在(2)的条件下,若已知商家每副护肘的进价为15元,每副护膝的进价为20元,为支持学校的冰上运动,该商家准备正好用去方案中的最大利润的10%再次购进两种护具赠送给学校,请直接写出最多可赠送护膝多少副?26. 如图,在平面直角坐标系中A(0,2),B(﹣1,0),以点A为直角顶点,AB为直角边在第二象限内作等腰直角△ABC.
(1)、将等边△BEF旋转至如图①所示位置时,求证:CE=BE+AE;(2)、将等边△BEF顺时针旋转至如图②、图③位置时,请分别直接写出AE,BE,CE之间的数量关系,不需要证明;(3)、在(1)和(2)的条件下,若BF=4,AE=1,则CE= .25. 为了更安全地开展冰上运动某校决定购进一批护肘及护膝.已知用900元购进护膝的数量比用400元购进护肘的数量多10副,且每副护膝价格是每副护肘价格的1.5倍.(1)、每副护肘和护膝的价格分别是多少元;(2)、若学校决定用不超过8000元购进两种护具共300副,且护肘数量不多于102副,求有哪几种购买方案;(3)、在(2)的条件下,若已知商家每副护肘的进价为15元,每副护膝的进价为20元,为支持学校的冰上运动,该商家准备正好用去方案中的最大利润的10%再次购进两种护具赠送给学校,请直接写出最多可赠送护膝多少副?26. 如图,在平面直角坐标系中A(0,2),B(﹣1,0),以点A为直角顶点,AB为直角边在第二象限内作等腰直角△ABC. (1)、设点C的坐标为(a,b),求a+b的值.(2)、求四边形OACB的面积.(3)、在(1)的条件下,坐标平面内是否存在一点P(不与点C重合),使△PAB与△ABC全等?若存在,直接写出P点坐标;若不存在,请说明理由.
(1)、设点C的坐标为(a,b),求a+b的值.(2)、求四边形OACB的面积.(3)、在(1)的条件下,坐标平面内是否存在一点P(不与点C重合),使△PAB与△ABC全等?若存在,直接写出P点坐标;若不存在,请说明理由.