广东省深圳市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-02-23 类型：期末考试

进入出卷网下载

一、单选题

1. 中宁县位于宁夏回族自治区中部西侧，是世界枸杞的发源地和正宗原产地，已有600多年的历史.1995年被国务院命名为“中国枸杞之乡”；将“中国枸杞之乡”六个字分别写在一个正方体的六个面上，这个正方体的展开图如图所示，那么在这个正方体中，和“杞”字相对的字是（）

A、中 B、国 C、枸 D、乡

查看试题解析
2. 如图，矩形 $A B O C$ 的顶点坐标为 $(- 4 ， 5)$ ， D是 $O B$ 的中点，E为 $O C$ 上的一点，当 $Δ A D E$ 的周长最小时，点E的坐标是（）

A、 $(0 ， \frac{4}{3})$ B、 $(0 ， \frac{5}{3})$ C、 $(0 ， 2)$ D、 $(0 ， \frac{10}{3})$

查看试题解析
3. 下列各式：① $\sqrt{2}$ ，② $\sqrt{\frac{1}{3}}$ ，③ $\sqrt{8}$ ，④ $\sqrt{0.5}$ ，⑤ $\sqrt{x^{2} + 1}$ 中，最简二次根式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 用图象法解某二元一次方程组时，在同一直角坐标系中作出相应的两个一次函数的图象（如图所示），则所解的二元一次方程组是（）

A、 ${\begin{matrix} x + y - 2 = 0 ， \\ 3 x - 2 y - 1 = 0 \end{matrix}$ B、 ${\begin{matrix} 2 x - y - 1 = 0 ， \\ 3 x - 2 y - 1 = 0 \end{matrix}$ C、 ${\begin{matrix} 2 x - y - 1 = 0 ， \\ 3 x + 2 y - 5 = 0 \end{matrix}$ D、 ${\begin{matrix} x + y - 2 = 0 ， \\ 2 x - y - 1 = 0 \end{matrix}$

查看试题解析
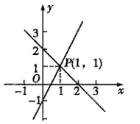5. 下列说法中，正确的是（）

A、“从一副扑克牌（含大小王）中抽一张，恰好是红心A”是随机事件 B、“三角形两边之和大于第三边"是随机事件 C、“车辆到达路口，遇到红灯”是不可能事件 D、“任意画一个三角形，其内角和是360°”是必然事件

查看试题解析
6. 用A、B两种规格的长方形纸板（如图1）无重合无缝隙的拼接可得如图2所示的周长为40cm的正方形，已知A种长方形的宽为1cm，则B种长方形的面积是（　　）

A、 $12 c m^{2}$ B、 $14 c m^{2}$ C、 $21 c m^{2}$ D、 $28 c m^{2}$

查看试题解析
7. 一次函数 $y = 2 x + 1$ 与二次函数 $y = x^{2} - 4 x + 3$ 的图象交点（　　）

A、只有一个 B、恰好有两个 C、可以有一个，也可以有两个 D、无交点

查看试题解析
8. 如图，已知圆柱底面的周长为8dm，圆柱高为3dm，在圆柱的侧面上，过点A和点C嵌有一圈金属丝，则这圈金属丝的周长最小为（）dm.

A、11 B、 $2 \sqrt{55}$ C、 $2 \sqrt{73}$ D、10

查看试题解析
9. 下列说法中正确的有（）
⑴两条直线被第三条直线所截，同位角相等；
⑵若 $∠ 1 + ∠ 2 + ∠ 3 = 90 °$ ，则 $∠ 1$ ， $∠ 2$ ， $∠ 3$ 互余；
⑶相等的两个角是对顶角；
⑷从直线外一点到这条直线的垂线段，叫做这点到直线的距离．

A、 $0$ 个 B、 $1$ 个 C、 $2$ 个 D、 $3$ 个

查看试题解析
10. 甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．则下列结论：
①A，B两城相距 $300$ 千米；
②乙车比甲车晚出发 $1$ 小时，却早到 $1$ 小时；
③乙车出发后 $1.5$ 小时追上甲车；
④当甲、乙两车相距 $50$ 千米时， $t = \frac{5}{4}$ 或 $\frac{15}{4}$
其中正确的结论有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析

二、填空题

11. 在实数 $\frac{22}{7}$ ， -2 ， $\sqrt{4}$ ， $\sqrt{2}$ ，3.14 ， $\sqrt[3]{- 27}$ ， $\frac{π}{5}$ ，这7个数中，其中无理数是

查看试题解析
12. 若 ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$ 是二元一次方程 $x - a y = 2$ 的解，则 $a =$ ．

查看试题解析
13. 计算： $2^{- 2} + \sqrt{4} - | - 3 | =$ ．

查看试题解析
14. 已知 $△ A B C$ 的三个内角的度数之比 $∠ A$ ： $∠ B$ ： $∠ C = 1$ ： $3$ ： $5$ ，则 $∠ B =$ 度， $∠ C =$ 度．

查看试题解析
15. 已知点(−2，y₁)，(−1，y₂)，(1，y₃)都在直线y=− $\frac{1}{3}$ x+b上，则y₁ ， y₂ ， y₃的值的大小关系是．

查看试题解析

三、解答题

16. 计算： $| \sqrt{2} - \sqrt{3} | + \sqrt{8}$ .

查看试题解析
17. 解方程组： ${\begin{array}{l} x - y = 5 ① \\ 3 x - y = - 1 ② \end{array}$

查看试题解析
18. 某班为了解班级同学寒假期间在家进行体育锻炼的情况，通过钉钉线上运动打卡活动，统计了班级40名同学一段时间的运动打卡次数如表：

打卡次数

6

8

9

10

12

14

15

人数

3

5

4

11

5

4

8

(1)、求这40名同学打卡次数的平均数；

(2)、为了调动大多数同学锻炼的积极性，班主任准备制定一个打卡奖励标准，凡打卡次数达到或超过这个标准的同学将获得奖励的措施.如果你是班主任，从平均数、中位数、众数的角度进行分析，你将如何确定这个“打卡奖励”标准?

查看试题解析
19. 如图，在△ABC中，AB=AC，D为BC中点，AE∥BD，O是CE的中点。

(1)、求证：四边形AEBD是矩形；

(2)、连接CE交AB于点F，若BE=2 $\sqrt{3}$ ，AE=2，求EF的长。

查看试题解析
20. 小明从家到学校的路程为3.3千米，其中有一段上坡路，平路，和下坡路．如果保持上坡路每小时行3千米．平路每小时行4千米，下坡路每小时行5千米．那么小明从家到学校用一个小时，从学校到家要44分钟，求小明家到学校上坡路、平路、下坡路各是多少千米？

查看试题解析
21. 如图，⊙O的半径为5，点A在⊙O上，过点A的直线l与⊙O相交于点B，AB＝6，以直线l为图象的一次函数解析式为y＝kx﹣8k（k为常数且k≠0）．

(1)、求直线l与x轴交点的坐标；

(2)、求点O到直线AB的距离；

(3)、求直线AB与y轴交点的坐标．

查看试题解析
22. 如图，在△ABC中，AB＝AC，D为BC中点．四边形ABDE是平行四边形．

求证：四边形ADCE是矩形

查看试题解析

打卡次数	6	8	9	10	12	14	15
人数	3	5	4	11	5	4	8