广东省梅州市大埔县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-02-23 类型：期末考试

进入出卷网下载

一、单选题

1. 9的平方根是（）

A、3 B、 $\pm 3$ C、 $- 3$ D、 $\pm 2$

查看试题解析
2. 设三角形的三边长分别等于下列各组数，能构成直角三角形的是（）

A、 $\sqrt{2}$ ， $\sqrt{3}$ ， $\sqrt{5}$ B、 $\frac{1}{3}$ ， $\frac{1}{4}$ ， $\frac{1}{5}$ C、 $\frac{1}{6}$ ， $\frac{1}{8}$ ， $\frac{1}{10}$ D、4，5，6

查看试题解析
3. 某校八年级进行了三次数学测试，甲、乙、丙、丁4名同学三次数学成绩的平均分都是109分，方差分别是 ${S_{甲}}^{2} = 3.6 ， {S_{乙}}^{2} = 4.6 ， {S_{丙}}^{2} = 6.3 ， {S_{丁}}^{2} = 7.3$ ，则这4名同学三次数学成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 在平面直角坐标系的第二象限内有一点P，点P到x轴的距离为2，到y轴的距离为3，则点P的坐标是（）

A、 $(2 ， - 3)$ B、 $(3 ， - 2)$ C、 $(- 3 ， 2)$ D、 $(- 2 ， 3)$

查看试题解析
5. 如图，AB∥CD，∠A＝30°，∠F＝40°，则∠C＝（）

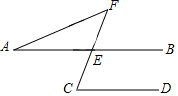A、65° B、70° C、75° D、80°

查看试题解析
6. 下列命题是真命题的是（）

A、在平面直角坐标系中，点P(-3，0)在y轴上 B、在一次函数y= -2x+3中，y随着x的增大而增大 C、同旁内角互补 D、若 $\sqrt{x - 2} + \sqrt{y + 3} = 0$ ，则x+y=-1

查看试题解析
7.
在平面直角坐标系中，一次函数y=kx+b的图象如图所示，观察图象可得（）

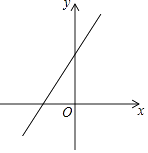A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜0

查看试题解析
8. 无论m为何实数．直线 $y = x + 2 m$ 与 $y = - x + 4$ 的交点不可能在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
9. 篮球联赛中，每场比赛都要分出胜负，每队胜 $1$ 场得 $2$ 分，负 $1$ 场得 $1$ 分，某队在 $10$ 场比赛中得到 $16$ 分．若设该队胜的场数为 $x$ ，负的场数为 $y$ ，则可列方程组为（）

A、 ${\begin{array}{l} x + y = 10 \\ 2 x + y = 16 \end{array}$ B、 ${\begin{array}{l} x + y = 10 \\ 2 x - y = 16 \end{array}$ C、 ${\begin{array}{l} x + y = 10 \\ x - 2 y = 16 \end{array}$ D、 ${\begin{array}{l} x + y = 10 \\ x + 2 y = 16 \end{array}$

查看试题解析
10. 甲、乙两人相约从A地到B地，甲骑自行车先行，乙开车，两人均同一路线上速匀行驶，乙到B地后即停车等甲.甲、乙两人之间的距离y（千米）与甲行驶的时间x（小时）之间的函数关系如图所示，则乙从A地到B地所用的时间为（）

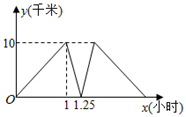A、0.25小时 B、0.5小时 C、1小时 D、2.5小时

查看试题解析

二、填空题

11. 教室里，从前面数第8行第3位的学生位置记作 $(8 ， 3)$ ，则坐在第3行第8位的学生位置可表示为．

查看试题解析
12. 计算：|﹣2|﹣ $\sqrt[3]{27}$ ＝．

查看试题解析
13. 数据3、1、x、 $- 1$ 、 $- 3$ 的平均数是1，则这组数据的中位数是．

查看试题解析
14. 如图，在四边形 $A B D C$ 中， $C D // A B$ ， $A C ⊥ B C$ 于点 $C$ ，若 $∠ A = 40 °$ ，则 $∠ D C B$ 的度数为°．

查看试题解析
15. 点 $P (a ， b)$ 在函数 $y = 3 x + 2$ 的图象上，则代数式 $3 a - b + 1$ 的值等于．

查看试题解析
16. 如图，有一四边形空地ABCD，AB⊥AD，AB＝3，AD＝4，BC＝12，CD＝13，则四边形ABCD的面积为.

查看试题解析
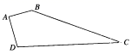17. $\sqrt{3}$ 的整数部分是a，小数部分是b，计算a﹣2b的值是.

查看试题解析

三、解答题

18. 计算：

(1)、 $(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2}) - \sqrt{25}$

(2)、 $| - \sqrt{3} | - (4 - π)^{0} - \sqrt{24} \div \sqrt{8} + {(\frac{1}{4})}^{- 1}$

查看试题解析
19. 如图，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A=37º，求∠D的度数

查看试题解析
20. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（-4，5），（-1，3）．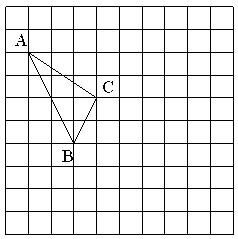

( 1 )请在如图所示的网格平面内作出平面直角坐标系；

( 2 )请作出△ABC关于y轴对称的△A′B′C′；

( 3 )写出点B′的坐标．

查看试题解析
21. 解方程组：

(1)、 ${\begin{array}{l} 6 x - 5 y = 3 \\ 6 x + y = - 15 \end{array}$

(2)、 ${\begin{array}{l} x + 4 y = 14 \\ \frac{x - 3}{4} - \frac{y - 3}{3} = \frac{1}{12} \end{array}$

查看试题解析
22. 为进一步提高学生学习数学的兴趣，某校开展了一次数学趣味知识竞赛，并随机抽取了50名学生的竞赛成绩（竞赛成绩为百分制，本次竞赛没有满分），经过整理数据得到以下信息：
信息一：50名学生竞赛成绩频数分布直方图如图所示，从左到右依次为第一组到第五组（每组数据含左端点值，不含右端点值）．

信息二：第三组的成绩（单位：分）为：

74 71 73 74 79 76 77 76 76 73 72 75

根据信息解答下列问题：

(1)、第二组的学生人数是人；

(2)、第三组竞赛成绩的众数是分，抽取的50名学生竞赛成绩的中位数是分；

(3)、若该校共有1500名学生参赛，请估计该校参赛学生成绩不低于80分的有多少人？

查看试题解析
23. 列二元一次方程组解应用题：
小颖家离学校1880米，其中有一段为上坡路，另一段为下坡路.她跑步去学校共用了16分钟，已知小颖在上坡路上的平均速度是80米/分钟，在下坡路上的平均速度是200米/分钟.求小颖上坡、下坡各用了多长时间？

查看试题解析
24. 已知一次函数y=kx+b的图象经过点A（-4，0），B（2，6）两点.

(1)、求一次函数y=kx+b的表达式；

(2)、在直角坐标系中，画出这个函数的图象；

(3)、求这个一次函数与坐标轴围成的三角形面积.

查看试题解析
25. 在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， C B = C A = 2 \sqrt{2}$ ，点D是线段 $A B$ 上一点，连接 $C D$ ，在 $C D$ 右侧作 $∠ D C E = 90 °$ ，且 $C E = C D$ ，连接 $A E$ ，已知 $A E = 1$ ．

(1)、求 $∠ C A E$ 的度数；

(2)、求 $C D$ 的长；

查看试题解析