广东省广州市南沙区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-02-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，不具有稳定性的是（）

A、等腰三角形 B、平行四边形 C、锐角三角形 D、等边三角形

查看试题解析
2. 下面的轴对称图形中，对称轴数量最多的是（）

A、 B、 C、 D、

查看试题解析
3. 下面的计算正确的是（）

A、（ab）²＝ab² B、（ab）²＝2ab C、a³•a⁴＝a¹² D、（a³）⁴＝a¹²

查看试题解析
4. 当x＝﹣2时，下列分式没有意义的是（）

A、 $\frac{x - 2}{x + 2}$ B、 $\frac{x}{x - 2}$ C、 $\frac{x + 2}{2 x}$ D、 $\frac{x - 2}{- 2 x}$

查看试题解析
5. 如图是两个全等三角形，图中的字母表示三角形的边长，则∠1的度数是（）

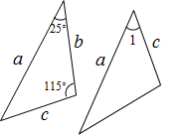A、115° B、65° C、40° D、25°

查看试题解析
6. 计算（2x﹣1）（x＋2）的结果是（）

A、2x²＋x﹣2 B、2x²﹣2 C、2x²﹣3x﹣2 D、2x²＋3x﹣2

查看试题解析
7. 等腰三角形的一边长是5，另一边长是10，则周长为（）

A、15 B、20 C、20或25 D、25

查看试题解析
8. 如图，Rt△ABC中，∠C＝90°，AD平分∠BAC，交BC于点D，CD＝6，AB＝12，则△ABD的面积是（）

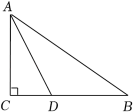A、18 B、24 C、36 D、72

查看试题解析
9. 如图，将△ABC沿着DE减去一个角后得到四边形BCED，若∠BDE和∠DEC的平分线交于点F，∠DFE＝α，则∠A的度数是（）

A、180°﹣α B、180°﹣2α C、360°﹣α D、360°﹣2α

查看试题解析
10. 若正整数m使关于x的分式方程 $\frac{m}{(x + 2) (x - 1)} = \frac{x}{x + 2} - \frac{x - 2}{x - 1}$ 的解为正数，则符合条件的m的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 红细胞也称红血球，是血液中数量最多的一种血细胞，也是我们体内通过血液运送氧气的最主要的媒介，同时还具有免疫功能．红细胞的直径单位一般用微米（μm），1μm＝0.000001m，人类的红细胞直径通常是6μm～8μm.6μm用科学记数法可以表示为m．

查看试题解析
12. 在一场足球比赛中，运动员甲、乙两人与足球的距离分别是8m，17m，那么甲、乙两人的距离d的范围是．

查看试题解析
13. 化简： $\frac{3 y}{2 x - 2 y} + \frac{2 x y}{x^{2} - x y}$ 的计算结果是．

查看试题解析
14. 把多项式x²﹣6x＋m分解因式得（x＋3）（x﹣n），则m＋n的值是．

查看试题解析
15. 如图，在四边形中ABCD中，BD平分∠ABC，∠DAB＋∠DCB＝180°，DE⊥AB于点E，AB＝8，BC＝4，则BE的长度是．

查看试题解析
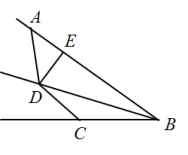16. 若|2x﹣4|＋（y＋3）²＝0，点A（x，y）关于x轴对称的点为B，点B关于y轴对称的点为C，则点C的坐标是．

查看试题解析

三、解答题

17. 计算：（结果用幂的形式表示）3x²•x⁴﹣（﹣x³）²

查看试题解析
18. 已知一个正多边形一个内角等于一个外角的 $\frac{3}{2}$ 倍，求这个正多边形的边数．

查看试题解析
19. 如图，已知∠A＝∠C，AE、CF分别与BD交于点E、F．请你从下面三项中再选出两个作为条件，另一个作为结论，写出一个真命题，并加以证明．①AB∥DC；②AE∥CF；③DE＝BF．

查看试题解析
20. 如图，在△ABC中，

(1)、尺规作图：作边AC的垂直平分线，交AB于点D，交AC于点E，连结CD．

(2)、若△BCD的周长等于18，AE＝4，求△ABC的周长．

查看试题解析
21. 已知T＝ $(m + \frac{4 m + 4}{m}) \cdot \frac{m^{2}}{m + 2}$ ．

(1)、化简T．

(2)、若m²＋2m﹣3＝0，求此时T的值．

查看试题解析
22. 为了响应打赢“蓝天保卫战”的号召，黄老师上下班的交通方式由驾车改为骑自行车，黄老师家距离学校的路程是9千米，在相同的路线上，驾车的平均速度是骑自行车的平均速度的3倍，所以黄老师每天上班要比开车早出发20分钟，才能按原驾车的时间到达学校．

(1)、求黄老师驾车的平均速度；

(2)、据测算，黄老师的汽车在上下班行驶过程中平均每小时碳排放量约为2.4千克，按这样计算，求黄老师一天（按一个往返计算）可以减少的碳排放量．

查看试题解析
23. 常见的分解因式的方法有提公因式法、公式法及十字相乘法，而有的多项式既没有公因式，也不能直接运用公式分解因式，但是某些项通过适当的调整能构成可分解的一组，用分组来分解一个多项式的因式，这种方法叫分组分解法．如x²＋2xy＋y²﹣16，我们细心观察这个式子就会发现，前三项符合完全平方公式，分解后与后面的部分结合起来又符合平方差公式，可以继续分解，过程为：x²＋2xy＋y²﹣16＝（x＋y）²﹣42＝（x＋y＋4）（x＋y﹣4）．它并不是一种独立的因式分解的方法，而是为提公因式或运用公式分解因式创造条件．阅读材料并解答下列问题：

(1)、分解因式：2a²﹣8a＋8；

(2)、请尝试用上面的方法分解因式：x²﹣y²＋3x﹣3y；

(3)、若△ABC的三边a，b，c满足a²﹣ab﹣ac＋bc＝0，请判断△ABC的形状并加以说明．

查看试题解析
24. 如图①，在△ABC中，∠ABC和∠ACB的平分线交于点O，∠A＝α．

(1)、如图①，若∠A＝50°，求∠BOC的度数．

(2)、如图②，连接OA，求证：OA平分∠BAC．

(3)、如图③，若射线BO与∠ACB的外角平分线交于点P，求证OC⊥PC．

查看试题解析
25. 在长方形ABCD中，AB＝4，BC＝8，点P、Q为BC边上的两个动点（点P位于点Q的左侧，P、Q均不与顶点重合），PQ＝2

(1)、如图①，若点E为CD边上的中点，当Q移动到BC边上的中点时，求证：AP＝QE；

(2)、如图②，若点E为CD边上的中点，在PQ的移动过程中，若四边形APQE的周长最小时，求BP的长；

(3)、如图③，若M、N分别为AD边和CD边上的两个动点（M、N均不与顶点重合），当BP＝3，且四边形PQNM的周长最小时，求此时四边形PQNM的面积．

查看试题解析