安徽省合肥市肥西县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-02-23 类型:期末考试
一、单选题
-
1. 点P在第二象限内,点P到x轴的距离是6,到y轴的距离是2,那么点P的坐标为( )A、(﹣6,2) B、(﹣2,﹣6) C、(﹣2,6) D、(2,﹣6)2. 下列四个图形中,是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 3. 下列各曲线中不能表示y是x的函数是( )A、
3. 下列各曲线中不能表示y是x的函数是( )A、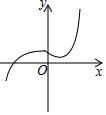 B、
B、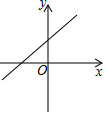 C、
C、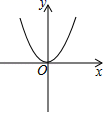 D、
D、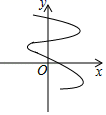 4. 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组 的解为( )
4. 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组 的解为( ) A、 B、 C、 D、5. 人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A、 B、 C、 D、5. 人字梯中间一般会设计一“拉杆”,这样做的道理是( ) A、两点之间,线段最短 B、垂线段最短 C、两直线平行,内错角相等 D、三角形具有稳定性6. 一个三角形的两边长分别为5和9,设第三边上的中线长为x,则x的取值范围是( )A、x>5 B、x<7 C、4<x<14 D、2<x<77. 如图,D在AB上,E在AC上,且∠B=∠C,则下列条件中,无法判定△ABE≌△ACD的是( )
A、两点之间,线段最短 B、垂线段最短 C、两直线平行,内错角相等 D、三角形具有稳定性6. 一个三角形的两边长分别为5和9,设第三边上的中线长为x,则x的取值范围是( )A、x>5 B、x<7 C、4<x<14 D、2<x<77. 如图,D在AB上,E在AC上,且∠B=∠C,则下列条件中,无法判定△ABE≌△ACD的是( ) A、AD=AE B、AB=AC C、BE=CD D、∠AEB=∠ADC8. 如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
A、AD=AE B、AB=AC C、BE=CD D、∠AEB=∠ADC8. 如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( ) A、4 B、5 C、6 D、79. 如图,点A,C,D,E在RtMON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD且BC=CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为( )
A、4 B、5 C、6 D、79. 如图,点A,C,D,E在RtMON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD且BC=CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为( ) A、30 B、50 C、66 D、8010. 如图,已知A,B两地相距4千米,上午11:00,甲从A地出发步行到B地,11:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离(千米)与甲所用时间(分)之间的关系如图所示,由图中的信息可知,乙到达A地的时间为( )
A、30 B、50 C、66 D、8010. 如图,已知A,B两地相距4千米,上午11:00,甲从A地出发步行到B地,11:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离(千米)与甲所用时间(分)之间的关系如图所示,由图中的信息可知,乙到达A地的时间为( ) A、上午11:40 B、上午11:35 C、上午11:45 D、上午11:50
A、上午11:40 B、上午11:35 C、上午11:45 D、上午11:50二、填空题
-
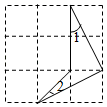
11. 函数中,自变量的取值范围是 .12. 如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=.
 13. 根据如图所示的程序计算函数值,若输入x的值为 , 则输出的y值为 .
13. 根据如图所示的程序计算函数值,若输入x的值为 , 则输出的y值为 . 14. 当三角形中一个内角β是另外一个内角α的时,我们称此三角形为“友好三角形”,α为友好角.如果一个“友好三角形”中有一个内角为42°,那么这个“友好三角形”的“友好角α”的度数为 .15. 若直线下移后经过点(5,1),则平移后的直线解析式为 .16. 如图,在△ABC中,AB=AC=5,S△ABC=12,AD⊥BC于点D,CE⊥AB于点E.若点P是AD上一动点,连接PE,PB,则PE+PB的最小值是 .
14. 当三角形中一个内角β是另外一个内角α的时,我们称此三角形为“友好三角形”,α为友好角.如果一个“友好三角形”中有一个内角为42°,那么这个“友好三角形”的“友好角α”的度数为 .15. 若直线下移后经过点(5,1),则平移后的直线解析式为 .16. 如图,在△ABC中,AB=AC=5,S△ABC=12,AD⊥BC于点D,CE⊥AB于点E.若点P是AD上一动点,连接PE,PB,则PE+PB的最小值是 .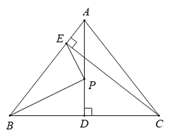
三、解答题
-
17. 已知一次函数y=kx﹣4,当x=3时,y=﹣1,求它的解析式以及该直线与坐标轴的交点坐标.18. 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,的顶点均在格点上,点C的坐标是 .

( 1 )将沿x轴正方向平移3个单位得到 , 画出 , 并写出点的坐标;
( 2 )画出关于x轴对称的 , 并求出的面积.
19. 如图所示,在△ABC中,点D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=66°,求∠DAC的度数. 20. 已知,如图,AB=AE,ABDE,∠ECB=65°,∠D=115°,求证:ABC≌EAD.
20. 已知,如图,AB=AE,ABDE,∠ECB=65°,∠D=115°,求证:ABC≌EAD. 21. 如图,一次函数y=kx+b(k≠0)的图象经过A,B两点.
21. 如图,一次函数y=kx+b(k≠0)的图象经过A,B两点. (1)、求此一次函数的解析式;(2)、结合函数图象,直接写出关于x的不等式kx+b<4的解集.22. 肥西县祥源花世界管理委员会要添置办公桌椅A,B两种型号,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.(1)、直接写出A型桌椅每套元,B型桌椅每套元;(2)、若管理委员会需购买两种型号桌椅共20套,若需要A型桌椅不少于12套,B型桌椅不少于6套,平均每套桌椅需要运费10元.设购买A型桌椅x套,总费用为y元.
(1)、求此一次函数的解析式;(2)、结合函数图象,直接写出关于x的不等式kx+b<4的解集.22. 肥西县祥源花世界管理委员会要添置办公桌椅A,B两种型号,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.(1)、直接写出A型桌椅每套元,B型桌椅每套元;(2)、若管理委员会需购买两种型号桌椅共20套,若需要A型桌椅不少于12套,B型桌椅不少于6套,平均每套桌椅需要运费10元.设购买A型桌椅x套,总费用为y元.①求y与x之间的函数关系,并直接写出x的取值范围;
②求出总费用最少的购置方案.
23. 在ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作ADE,使AE=AD,∠DAE=∠BAC,连接CE.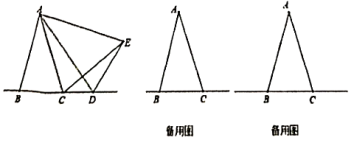 (1)、如图,当点D在BC延长线上移动时,若∠BAC=26°,则∠DCE= .(2)、设∠BAC=α,∠DCE=β.
(1)、如图,当点D在BC延长线上移动时,若∠BAC=26°,则∠DCE= .(2)、设∠BAC=α,∠DCE=β.①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B,C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.