安徽省蚌埠市经开区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-02-23 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，将点A（﹣3，﹣2）向右平移5个单位长度得到的点坐标为（）

A、（2，2） B、（﹣2，2） C、（﹣2，﹣2） D、（2，﹣2）

查看试题解析
2. 以下四个标志，每个标志都有图案和文字说明，其中的图案是轴对称图形是（）

A、 B、 C、 D、

查看试题解析
3. 下列事件中是必然事件的是（）

A、抛掷一枚质地均匀的硬币，正面朝上 B、随意翻到一本书的某页，这一页的页码是偶数 C、打开电视机，正在播放广告 D、任意画一个三角形，其内角和是180°

查看试题解析
4. 将一副三角板按如图方式重叠，则 $∠ 1$ 的度数为（）

A、 $45 °$ B、 $60 °$ C、 $75 °$ D、 $105 °$

查看试题解析
5. 下列命题是假命题的是（）

A、若 $a < 0$ ，则 $1 + a < 1 - a$ B、若 $a = 0$ ， $b = 0$ ，则 $a b = 0$ C、三角形的重心是这个三角形的三条角平分线的交点 D、等腰三角形顶角的平分线、底边上的中线、底边上的高相互重合

查看试题解析
6. 如图，点B ， F ， C ， E共线，∠B=∠E ， BF=EC ，添加一个条件，不能判断△ABC≌△DEF的是（）

A、AB=DE B、∠A=∠D C、AC=DF D、AC∥FD

查看试题解析
7. 如图，在 $△ A B C$ 中， $A B = A C$ ，分别以点A，B为圆心，大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧相交于点M和点N，作直线 $M N$ 分别交 $B C$ ､ $A B$ 于点D和点E，若 $∠ B = 50 °$ ，则 $∠ C A D$ 的度数是（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
8. 若一个等腰三角形的两边长分别为2、3，则这个等腰三角形的周长为(　　)．

A、7 B、8 C、6或8 D、7或8

查看试题解析
9. 甲无人机从地面起飞，乙无人机从距离地面20m高的楼顶起飞，两架无人机同时匀速上升10s．甲、乙两架无人机所在的位置距离地面的高度y（单位：m）与无人机上升的时间x（单位：s）之间的关系如图所示．下列说法正确的是（）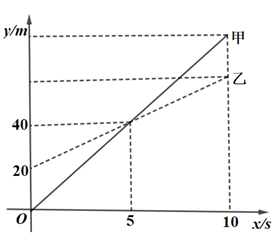

A、5s时，两架无人机都上升了40m B、10s时，两架无人机的高度差为20m C、乙无人机上升的速度为8m/s D、10s时，甲无人机距离地面的高度是60m

查看试题解析
10. 如图，在△ABC中，∠BAC＞90°，D为BC的中点，点E在AC上，将△CDE沿DE折叠，使得点C恰好落在BA的延长线上的点F处，连接AD、CF，则图中所有的等腰三角形的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 在函数y=x+1中，自变量x的取值范围是．

查看试题解析
12. 数形结合是解决数学问题常用的思想方法．如图，直线 $y = 2 x - 1$ 与直线 $y = k x + b (k \neq 0)$ 相交于点 $P (2 ， 3)$ ．根据图象可知，关于x的不等式 $2 x - 1 > k x + b$ 的解集是

查看试题解析
13. 如图，在△ABC中，∠A＝70°，∠C＝30°，点D为AC边上一点，过点D作DE∥AB，交BC于点E，且DE＝BE，则∠BDE的度数是．

查看试题解析
14. 中国古代数学家刘徽在《九章算术注》中，给出了证明三角形面积公式的出入相补法.如图所示，在 $△ A B C$ 中，分别取 $A B$ 、 $A C$ 的中点D、E，连接 $D E$ ，过点A作 $A F ⊥ D E$ ，垂足为F，将 $△ A B C$ 分割后拼接成矩形 $B C H G$ .若 $D E = 3 ， A F = 2$ ，则 $△ A B C$ 的面积是.

查看试题解析
15. 在平面直角坐标系中，点A（－2，4），点B（4，2），点P为x轴上一动点，当PA＋PB的值最小时，此时点P的坐标为．

查看试题解析

三、解答题

16. 如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABO的三个顶点坐标分别为A （－1，3）， B （－4，3），O （0，0）．
( 1 )△ABO向右平移5个单位，向上平移1个单位，得到△A₁B₁C₁ ，画出△A₁B₁C₁并写出点B₁的坐标；
( 2 )画出△A₁B₁C₁沿着x轴翻折后得到的△A₂B₂C₂ ，并写出点A₂的坐标．

查看试题解析
17. 已知：如图，AC，DB相交于点O，AB＝DC，∠ABO＝∠DCO．求证：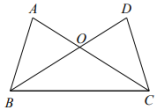

(1)、△ABO≌△DCO；

(2)、∠OBC＝∠OCB．

查看试题解析
18. 某学校护学岗值班，每天只需要一名家长.甲、乙两位家长从周一到周四这四天中各随机选择两天值班.

(1)、求甲恰好是连续的两天值班的概率；

(2)、甲、乙恰好都是连续的两天值班的概率是.

查看试题解析
19. 如图所示，已知AC∥BD，EA，EB分别平分∠CAB和∠DBA，CD过E点.求证：AB＝AC＋BD.

查看试题解析
20. 为了做好防疫工作，学校准备购进一批消毒液．已知A型消毒液7元/瓶，B型消毒液9元/瓶．学校准备购进这两种消毒液共90瓶．

(1)、写出购买所需总费用w元与A瓶个数x之间的函数表达式；

(2)、若B型消毒液的数量不少于A型消毒液数量的 $\frac{1}{3}$ ，请设计最省钱的购买方案，并求出最少费用．

查看试题解析
21. 如图，在△ABC和△CDE中，∠ACB＝∠DCE＝90°，AC＝BC，DC＝EC．过点C作CF⊥DE交DE于点F．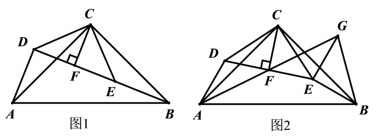

(1)、如图1，当点B、E、D在同一条线上时，
①求证： $C F = \frac{1}{2} D E$ ；
②求∠BDA的度数；

(2)、如图2，连接AF并延长至点G，使AF＝GF，连接GE、GB，试判断△BEG形状，并说明理由．

查看试题解析