浙江省舟山市普陀区2021-2022学年九年级上学期数学期末检测卷

试卷更新日期：2022-02-22 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分。）

1. 气象台预报明天下雨的概率为70%，则下列理解正确的是（）

A、明天30%的地区不会下雨 B、明天下雨的可能性较大 C、明天70%的时间会下雨 D、明天下雨是必然事件

查看试题解析
2. 如图，点 $A$ 、 $B$ 、 $C$ 在⊙O上， $A B // O C$ ， $∠ A = 70 °$ ，则 $∠ B$ 的度数是（）

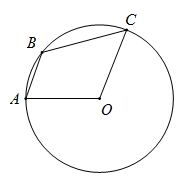A、110° B、125° C、135° D、165°

查看试题解析
3. 如图，若正六边形绕着中心 $O$ 旋转角 $α$ 得到的图形与原来的图形重合，则 $α$ 最小值为（）

A、 B、 C、 D、

查看试题解析
4. 已知函数 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴为直线 $x = - 4$ ．若 $x_{1} ， x_{2}$ 是方程 $a x^{2} + b x + c = 0$ 的两个根，且 $x_{1} < x_{2} ， 1 < x_{2} < 2$ ，则下列说法正确的是（）

A、 $x_{1} x_{2} > 0$ B、 $- 10 < x_{1} < - 9$ C、 $b^{2} - 4 a c < 0$ D、 $a b c > 0$

查看试题解析
5. 如图，在△ABC中，∠BAC＝90°，AB＝AC＝4 $\sqrt{2}$ ，以点C为中心，把△ABC逆时针旋转45°，得到△A′B′C，则图中阴影部分的面积为（　　）

A、2 B、2π C、4 D、4π

查看试题解析
6. 如图，小王在高台上的点A处测得塔底点C的俯角为α，塔顶点D的仰角为β，已知塔的水平距离AB＝a，则此时塔高CD的长为（）

A、asinα+asin β B、atanα+atan β C、 $\frac{a}{t a n a + t a n β}$ D、 $\frac{a t a n a t a n β}{t a n β}$

查看试题解析
7. 如图，AB是 $⊙ O$ 的弦（非直径），点C是弦AB上的动点（不与点A，B重合），过点C作垂直于OC的弦DE.设 $⊙ O$ 的半径为r，弦AB的长为a， $\frac{A C}{B C} = m$ ，则弦DE的长（）

A、与r，a，m的值均有关 B、只与r，a的值有关 C、只与r，m的值有关 D、只与a，m的值有关：

查看试题解析
8. 已知如图，点 C 是线段 AB 的黄金分割点（AC＞BC），则下列结论中正确的是（）

A、AB²＝AC²+BC² B、BC²＝AC•BA C、 $\frac{B C}{A C} = \frac{\sqrt{5} - 1}{2}$ D、 $\frac{A C}{B C} = \frac{\sqrt{5} - 1}{2}$

查看试题解析
9. “如果二次函数 $y = a x^{2} + b x + c$ 的图像与 $x$ 轴有两个交点，那么一元二次方程 $a x^{2} + b x + c = 0$ 有两个不相等的实数根．”请根据这句话的理解，解决以下问题；若 $m$ 、 $n (m < n)$ 是关于 $x$ 的方程 $1 - (x - a) (x - b) = 0$ 的两根，且 $a < b$ ，则 $a$ ， $b$ ， $m$ ， $n$ 的大小关关系是（）

A、 $m < a < b < n$ B、 $a < b < m < n$ C、 $a < m < b < n$ D、 $a < m < n < b$

查看试题解析
10. 如图，在半径为1的⊙O中，直径AB把⊙O分成上、下两个半圆，点C是上半圆上一个动点(C与点A，B不重合)，过点C作弦CD⊥AB，垂足为E，∠OCD的平分线交⊙O于点P，设CE＝x，AP＝y，下列图象中，最能刻画y与x的函数关系的图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题（本题有6小题，每题4分，共24分）

11. 若 $3 x = 2 y (y \neq 0)$ ，则 $\frac{x - y}{y} =$ ．

查看试题解析
12. 一抛物线的形状，开口方向与 $y = \frac{3}{2} x^{2} - 3 x + 1$ 相同，顶点在(-2，3)，则此抛物线的解析式为．

查看试题解析
13. 如图是一种手机三脚架，它通过改变锁扣C在主轴 $A B$ 上的位置调节三脚架的高度，其它支架长度固定不变．已知支脚 $D E = A B$ ，底座 $C D ⊥ A B ， B G ⊥ A B$ ，且 $C D = B G$ ，F是 $D E$ 上的固定点，且 $E F ： D F = 2 ： 3$ ．当点B，G，E三点在同一直线上（如图1所示）时，测得 $\tan ∠ B E D = 2$ ；若将点C向下移动 $24 cm$ ，则点B，G，F三点在同一直线上（如图2），此时点A离地面的高度是 $cm$ ．

查看试题解析
14. 如图， $A B$ 是 $⊙ O$ 的直径， $A C$ 是 $⊙ O$ 的切线，切点为A， $B C$ 交 $⊙ O$ 于点D，点E是 $A C$ 的中点．若 $⊙ O$ 的半径为2， $∠ B = 5 0^{∘}$ ， $A C = 4.8$ ，则阴影部分的面积为．

查看试题解析
15. 如图，在矩形 $A B C D$ 中， $A B = 6$ ， $A D = 8$ ．连接 $B D$ ， $∠ D B C$ 的角平分线 $B E$ 交 $D C$ 于点E，现把 $△ B C E$ 绕点B逆时针旋转，记旋转后的 $△ B C E$ 为 $△ B C^{'} E^{'}$ ．当射线 $B E^{'}$ 和射线 $B C^{'}$ 都与线段 $A D$ 相交时，设交点分别为F，G．若 $△ B F D$ 为等腰三角形，则线段 $D G$ 长为．

查看试题解析
16. 如图，已知抛物线 $y = - \frac{3}{16} (x + 4) (x - 4)$ 与 $x$ 轴交于 $A$ 、 $B$ 两点，与 $y$ 轴交于 $C$ 点， $⊙ C$ 的半径为2． $G$ 为 $⊙ C$ 上一动点， $P$ 为 $A G$ 的中点，则 $A G$ 的最小值为， $O P$ 的最大值为．

查看试题解析

三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）

17. 计算：

(1)、 $| - \sqrt{2} | - 2 s i n 45 ° + t a n 45 °$ .

(2)、 $4 s i n 30 ° c o s 60 ° - t a n^{2} 30 °$ .

查看试题解析
18. 舟山作为新晋的网红城市，旅游业快速发展，普陀区共有A、B、C、D、E等网红景点，区旅游部门统计绘制出2021年“国庆”长假期间旅游情况统计图（不完整）如下所示，根据相关信息解答下列问题：

舟山市普陀区2022国庆旅游情况统计图

(1)、2021年“国庆”长假期间，普陀区旅游景点共接待游客▲ 万人．并补全条形统计图；

(2)、在等可能性的情况下，甲、乙两个旅行团在A、B、C、D四个景点中选择去同一景点的概率是多少？请用画树状图或列表加以说明．

查看试题解析
19. 我国纸伞的制作工艺十分巧妙.如图1，伞不管是张开还是收拢，伞柄 $A P$ 始终平分同一平面内两条伞骨所成的角 $∠ B A C$ ，且 $A B = A C$ ，从而保证伞圈D能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图，此时伞圈D已滑动到点 $D^{'}$ 的位置，且A，B， $D^{'}$ 三点共线， $A D^{'} = 40 cm$ ，B为 $A D^{'}$ 中点，当 $∠ B A C = 140 °$ 时，伞完全张开.

(1)、求 $A B$ 的长.

(2)、当伞从完全张开到完全收拢，求伞圈D沿着伞柄向下滑动的距离.（参考数据： $\sin 70 ° \approx 094 ， \cos 70 ° \approx 0.34 ， \tan 70 ° \approx 2.75$ ）

查看试题解析
20. 如图，网格是由边长为1的小正方形组成，△ABC的每个顶点都在网格的交点上，将△ABC绕点A顺时针旋转90°后得到△AB₁C₁.

(1)、用无刻度的直尺画出△AB₁C₁：

(2)、求AB在旋转过程中扫过的面积（结果保留π）.

查看试题解析
21. 如图，在 $△ A B C$ 中， $A B = A C$ ，以底边 $B C$ 为直径的 $⊙ O$ 交两腰于点 $D$ ， $E$ .

(1)、求证： $B D = C E$ ；

(2)、当 $△ A B C$ 是等边三角形，且 $B C = 4$ 时，求 $\overset{⌢}{D E}$ 的长.

查看试题解析
22. 某商店在五一期间购进了600个旅游纪念品，进价每个6元，第一天以每个10元的价格售出了200个；第二天若以每个10元的价格仍可售出200个，但为了适当增加销量，决定降价销售，已知单价每降低1元，可多售出50个；第三天商店对剩下的旅游纪念品做清仓处理，以每个4元的价格全部售出．设第二天旅游纪念品单价降低x元 $(0 < x < 4)$ ，这批旅游纪念品的销售利润为y元（利润=售价-成本），请解决以下问题：

(1)、用含x的代数式表示第三天的销售量

(2)、若第三天销售量不超过前两天销售量之和的 $\frac{1}{5}$ ，求当第二天旅游纪念品的销售单价降低多少元时，这批旅游纪念品的销售总利润最大?最大值是多少？

查看试题解析
23. 二次函数 $y = 2 x^{2} + b x + c$ 的顶点 $M$ 是直线 $y_{1} = - \frac{3}{2} x$ 和直线 $y_{2} = x + m$ 的交点.

(1)、当 $x \geq 2$ 时， $y = 2 x^{2} + b x + c$ 的值均随 $x$ 的增大而增大，求 $m$ 的取值范围.

(2)、若直线 $y_{1}$ 与 $y_{2}$ 交于点 $(2 ， n)$ .
①当 $t \leq x \leq t + 1$ 时，二次函数的最小值为 $- 3$ ，求 $t$ 的取值范围.

② $P (x_{0} ， p)$ 和 $Q (3 ， q)$ 为二次函数上的两个点，当 $p < q$ 时，求 $x_{0}$ 的取值范围.

查看试题解析
24. 如图

(1)、（问题发现）
如图1，在Rt△ABC中，AB＝AC，D为BC边上一点（不与点B、C重合）将线段AD绕点A顺时针旋转90°得到AE，连结EC，则线段BD与CE的数量关系是，位置关系是；

(2)、（探究证明）
如图2，在Rt△ABC和Rt△ADE中，AB＝AC，AD＝AE，将△ADE绕点A旋转，当点C，D，E在同一直线时，BD与CE具有怎样的位置关系，并说明理由；

(3)、（拓展延伸）
如图3，在Rt△BCD中，∠BCD＝90°，BC＝2CD＝4，将△ACD绕顺时针旋转，点C对应点E，设旋转角∠CAE为α（0°＜α＜360°），当点C，D，E在同一直线时，画出图形，并求出线段BE的长度．

查看试题解析