浙江省绍兴市诸暨市2021-2022学年七年级上学期数学期末考试试卷

试卷更新日期：2022-02-22 类型：期末考试

进入出卷网下载

一、选择题（木大题共10小题，每小题3分，共30分。）

1. ﹣2022的相反数是（）

A、﹣2022 B、 $- \frac{1}{2022}$ C、2022 D、 $\frac{1}{2022}$

查看试题解析
2. 中国人最先使用负数，魏晋时期的数学家刘徽在其著作《九章算术注》中，用不同颜色的算筹（小棍形状的记数工具）分别表示正数和负数（红色为正，黑色为负）如图1表示的是（+2）+（﹣2），根据这种表示法，可推算出图2所表示的算式是（）

A、（+3）+（+6） B、（+3）+（﹣6） C、（﹣3）+（+6） D、（﹣3）+（﹣6）

查看试题解析
3. 下列说法中不正确的是（）

A、10的平方根是 $\pm \sqrt{10}$ B、8是64的一个平方根 C、﹣27的立方根是﹣3 D、 $\frac{4}{9}$ 的平方根是 $\frac{2}{3}$

查看试题解析
4. 已知3x⁶y²和x^3myⁿ是同类项，则2m﹣n的值是（）

A、6 B、5 C、4 D、2

查看试题解析
5. 如图1，A ， B两个村庄在一条河l（不计河的宽度）的两侧，现要建一座码头，使它到A、B两个村庄的距离之和最小，图2中所示的C点即为所求的码头的位置，那么这样做的理由是（）

A、两直线相交只有一个交点 B、两点确定一条直线 C、两点之间，线段最短 D、经过一点有无数条直线

查看试题解析
6. 解方程 $\frac{2 x + 1}{3} - \frac{10 x + 1}{6} = 1$ 时，去分母、去括号后，正确结果是（）

A、4x+1﹣10x+1=1 B、4x+2﹣10x﹣1=1 C、4x+2﹣10x﹣1=6 D、4x+2﹣10x+1=6

查看试题解析
7. 一个角加上20°后，等于这个角的余角，则这个角的度数是（）

A、35° B、45° C、60° D、80°

查看试题解析
8. 《增删算法统宗》记载：“有个学生资性好，一部孟子三日了，每日增添一倍多，问君每日读多少？”其大意是：有个学生天资聪慧，三天读完一部《孟子》，每天阅读的字数是前一天的两倍，问他实天各读多少个字？已知《孟子》一书共有34685个字，设他第一天读x个字，则下面所列方程正确的是（）

A、x+2x+4x＝34685 B、x+2x+3x＝34685 C、x+2x+2x＝34685 D、 $x + \frac{1}{2} x + \frac{1}{4} x = 34685$

查看试题解析
9. 如图是由两个正方形和一个妊径为a的姏圆组合而成的，已知两个正方形的边长分别为a、b（a＞b），则图中阴影部分面积为（）

A、 $a^{2} + b^{2} - \frac{{πa}^{2}}{2}$ B、 $a^{2} - b^{2} + \frac{{πa}^{2}}{2}$ C、 $a^{2} - b^{2} - \frac{{πa}^{2}}{2}$ D、a²﹣b²

查看试题解析
10. 现代的数学符号体系，不仅使得数学语言变得简洁明了，还能更好地帮助人们总结出便于运算的各种运算法则，简明地揭示数量之间的相互关系．我国在1905年清朝学堂的课本中还用“ $\frac{五}{丁^{二}}$ ⊺ $\frac{三}{丙^{二}}$ ⊥ $\frac{二七}{甲^{二} 乙^{二}}$ ”来表示相当于 $\frac{d^{2}}{5} - \frac{c^{2}}{3} + \frac{a^{2} b^{2}}{27}$ 的代数式，观察其中的规律，化简“ $\frac{六}{六乙^{二}}$ ⊥ $\frac{三}{乙^{二}}$ ⊺ $\frac{甲}{丙^{二}}$ ”后得（）

A、 $\frac{4 b^{2}}{3} - \frac{c^{2}}{a}$ B、 $\frac{2 b^{2}}{3} + \frac{c^{2}}{a}$ C、 $\frac{4}{b^{2}} - \frac{a}{c^{2}}$ D、 $\frac{- 2}{b^{2}} + \frac{a}{c^{2}}$

查看试题解析

二、填空题（本大题共10小题，每小题3分，共30分）

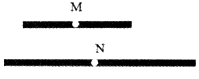
11. 用“＜”、“＞”或“＝”连接：﹣2 3．

查看试题解析
12. 1350000用科学记数法可表示为．

查看试题解析
13. 已知∠AOC和∠BOD是一组对顶角，若∠AOC＝40°，则∠BOD＝．

查看试题解析
14. $\sqrt{13}$ 的整数部分是．

查看试题解析
15. 用代数式表示“a与b的和的平方”为．

查看试题解析
16. 若一个数的平方等于6，则这个数等于．

查看试题解析
17. 若关于x的方程（k﹣3）x^|k^﹣2|+5k+1＝0是一元一次方程，则k＝．

查看试题解析
18. 某超市为回馈顾客，推出两种优惠方式：一、消费满60元，全部商品享八折优惠；二、消费满90元立减30元，消费者可以选择其中一种方式结账．小明用方式一结账，实际付款88元，若是他改用方式二结账，比起方式一能省下元．

查看试题解析
19. 如图，两根木条的长度分别为7cm和12cm，在它们的中点处各打一个小孔M、N（木条的厚度，宽度以及小孔大小均忽略不计）．将这两根木条的一端重合并放置在同一条直线上，则两小孔间的距离MN＝cm．

查看试题解析
20. 如图，在正方形ABCD内，将2张①号长方形纸片和3张②号长方形纸片按图1和图2两种方式放置（放置的纸片间没有重叠部分），正方形中未被覆盖的部分（阴影部分）的周长相等．

(1)、若①号长方形纸片的宽为1厘米，则②号长方形纸片的宽为厘米；

(2)、若①号长方形纸片的面积为10平方厘米，则②号长方形纸片的面积是平方厘米．

查看试题解析

三、解答题（木大题共6小题，共40分。）

21. 计算下列各题，并写出必要的计算步骤：

(1)、 $| - 2 | + \sqrt[3]{- 8} - \sqrt{9}$ ；

(2)、 $- 6 \times (\frac{1}{3} - \frac{1}{2})$ ．

查看试题解析
22. 解下列方程：

(1)、5x﹣1＝2x+2；

(2)、 $\frac{4 - y}{3} = \frac{1 + y}{2} - 1$ ．

查看试题解析
23. 先化简，再代入求值： $2 (a^{2} - ab) - 3 (\frac{2}{3} a^{2} - ab + 1)$ ，其中 $a = \frac{1}{4}$ ，b＝4．

查看试题解析
24. 如图，直线AB和直线CD交于O点，EO⊥AB，

(1)、若2∠EOC＝∠COB，求∠AOD的度数．

(2)、作OF⊥CD，证明：∠EOF＝∠COB．

查看试题解析
25. 定义：有A、B两只电子跳蚤在同一条数轴上跳动，它们在数轴上对应是实数分别为a、b．若实数a、b满足b＝3a+2时，则称A、B处于“和谐位置”，A、B之间的距离为“和谐距离”．

(1)、当A在原点位置，且A、B处于“和谐位置”时，“和谐距离”为．

(2)、当A、B之间的“和谐距离”为2022时，求a、b的值．

查看试题解析
26. 期末复习过程中，七（1）班的张老师设计了一个数学问题，涉及本册中多个知识点和多种数学思想，请聪明的你来解答一下吧．

(1)、若一个数x的立方等于﹣8，请求出x的值．

(2)、请利用整体思想和方程思想进行解题．
①若（1）中的x的值也是关于x的一元一次方程 $\frac{1}{2}$ x﹣3＝5x﹣p的解，那么关于y的一元一次方程 $\frac{1}{2}$ （y﹣8）﹣3＝5（y﹣8）﹣p的解为y＝ ▲ ．

②在如图所示的“幻方”中，每个小三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等，现将①中的x，y填入如图所示的位置，则（a﹣b）+（d﹣c）的值为多少？

(3)、在（2）的条件下，在数轴上标注x，y所表示的数的对应点，分别记作A，B，已知P点从A点出发，以1个单位每秒的速度向B点运动，Q点从B点出发，以4个单位每秒的速度在A、B两点之间做往返运动，P、Q两点同时开始运动，当Q点第一次返回到B点时，两点同时停止运动，若记数轴的原点为O，则P点运动几秒后OQ＝2OP？

查看试题解析