浙江省绍兴市诸暨市2021-2022学年八年级上学期数学期末考试试卷
试卷更新日期：2022-02-22 类型：期末考试
一、选择题（本大题有10小题，每小题3分，共30分。）
-
1. 篆体是我国古代汉字书体之一，下列篆体字“复”，“兴”，“之”，“路”中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 要说明命题“若a2＞b2 ， 则a＞b”是假命题，能举的一个反例是（ ）A、a＝3，b＝2 B、a﹣3，b＝2 C、a﹣＝3，b＝﹣1 D、a＝﹣1，b＝33. 三角形的两边长为4和8，则第三边长可能是（ ）A、3 B、4 C、8 D、124. 下列尺规作图分别表示：①作一个角的平分线，②作一条线段的垂直平分线．其中作法正确的是（ ）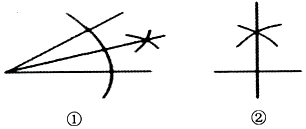
A、① B、② C、①② D、无5. 已知直角三角形的两条边长分别是3cm和4cm，则它的第三边长为（ ）A、4cm B、 cm C、5cm D、5cm或 cm6. 已知实数m＜1，则一次函数y＝（m﹣1）x+3﹣m图象经过的象限是（ ）A、一、二、三 B、二、三、四 C、一、三、四 D、一、二、四7. 一个装有进水管和出水管的容器，开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，每分钟的进水量和出水量是两个常数．容器内的水量y（单位：升）与时间x（单位：分）之间的关系如图，则8分钟时容器内的水量（单位：升）为（ ）
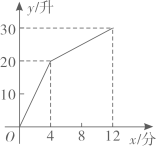A、24 B、25 C、26 D、278. 如图，△ABC≌△EDC，BC⊥CD，点A，D，E在同一条直线上，∠ACB＝25°，则∠ADC的度数是（ ）
A、45° B、60° C、75° D、70°9. 如图，正方形纸片ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上，这四条直线中相邻两条之间的距离依次为h1、h2、h3（h1＞0，h2＞0，h3＞0），若h1＝5，h2＝2，则正方形ABCD的面积S等于（ ）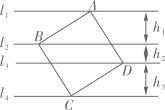
A、34 B、89 C、74 D、10910. 如图，在矩形纸片ABCD中，AB＝6，BC＝8，点M为AB上一点，将△BCM沿CM翻折至△ECM，ME与AD相交于点G，CE与AD相交于点F，且AG＝GE，则BM的长度是（ ）
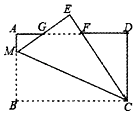A、 B、4 C、 D、5二、填空题（本大题有10小题，每小题3分，共30分）
-
11. 请用不等式表示“x的2倍与3的和小于1”： ．12. 函数y＝ 的自变量x的取值范围是.13. 点A（﹣3，4）到y轴的距离是 ．14. 若不等式组 的解集是﹣1＜x＜2，则a＝ ．15. 点A（﹣1，y1），B（3，y2）是直线y＝kx+b上的两点，若k＜0，则y1﹣y20（填“＞”或“＜”）．16. 如图，DE＝AC，∠1＝∠2，要使△DBE≌△ABC还需添加一个条件是 .（只需写出一种情况）
17. 如图所示为两个一次函数的图象，则关于x，y的方程 的解为 ．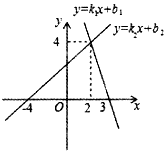
18. 如图，在平面直角坐标系中，将△OAB沿x轴向右平移后得到△O'A'B'，点A的坐标为（0，4），点A的对应点A在直线y x﹣1上，点B在∠A'AO的角平分线上，若四边形AA'B'B的面积为4，则点B的坐标为 ．
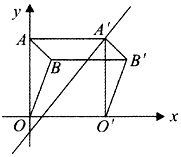19. 如图，在平面直角坐标系中，直线MN的函数解析式为y＝﹣x+3，点A在线段MN上且满足AN＝2AM，B点是x轴上一点，当△AOB是以OA为腰的等腰三角形时，则B点的坐标为 ．
20. 如图，等腰△BAC中，∠BAC＝120°，BC＝6，P为射线BA上的动点，M为BC上一动点，则PM+CP的最小值为 ．
三、解答题（第21、22题每题6分，23题8分，24、25题每题10分，共40分）
-
21. 解不等式（组）(1)、4x≤3x+7(2)、22. 如图，在6×6方格中，按下列要求画三角形，使它的顶点均在方格的顶点上（小正方形的边长为1）
(1)、在图甲中画一个面积为6的直角三角形；(2)、在图乙中画一个以AC为公共边的三角形与△ABC全等．23. 如图，BD＝BE，∠D＝∠E，∠ABC＝∠DBE＝90°，且点A，C，E在同一条直线上．
求证：
(1)、△DAB≌△ECB；(2)、作BF⊥AE于F，若AD＝3，AF＝1，求BE的长．24. 目前，全国各地都在积极开展新冠肺炎疫苗接种工作，某生物公司接到批量生产疫苗任务，要求5天内加工完成22万支疫苗，该公司安排甲，乙两车间共同完成加工任务，乙车间加工过程中停工一段时间维修设备，然后提高效率继续加工，直到与甲车间同时完成加工任务为止，设甲，乙两车间各白生产疫苗y（万支）与甲车间加工时间x（天）之间的关系如图1所示；两车间未生产疫苗W（万支）与甲车间加工时间x（天）之间的关系如图2所示，请结合图象回答下列问题：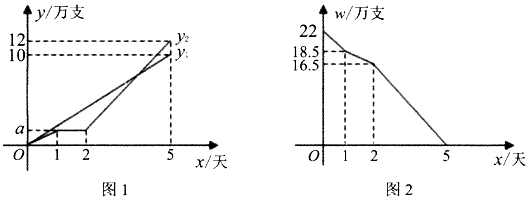
(1)、甲车间每天生产疫苗 万支，第一天甲、乙两车间共生产疫苗 万支，a＝；(2)、当x＝3时，求甲、乙车间生产的疫苗数（万支）之差y1﹣y2；(3)、若5.5万支疫苗恰好装满一辆货车，那么加工多长时间装满第一辆货车？再加工多长时间恰好装满第三辆货车？25. 如图，在平面直角坐标系中，A（2，0），B（0，6）．
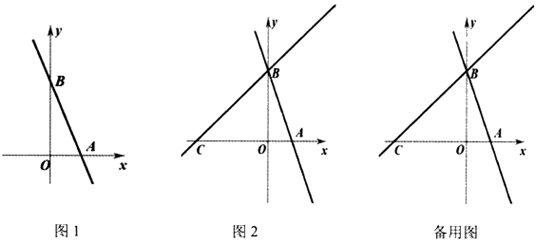(1)、如图1，过A，B两点作直线AB，求直线AB的解析式；(2)、如图2，点C在x轴负半轴上，C（﹣6，0），点P为直线BC上一点，若S△ABC＝2S△ABP ， 求满足条件的点P的坐标；(3)、在（2）的条件下，点E在直线BC上，点F在y轴上，当△AEF为一个等腰直角三角形时，请你直接写出E点坐标．