浙江省宁波市鄞州区2021-2022学年八年级上学期数学期末考试试卷

试卷更新日期：2022-02-22 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. 下列选项中的图标，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知a＜b，下列式子正确的是（）

A、a+3＞b+3 B、a﹣3＜b﹣3 C、﹣3a＜﹣3b D、 $\frac{a}{3} > \frac{b}{3}$

查看试题解析
3. 如图，△ABC≌△ADE，∠C＝40°，则∠E的度数为（）

A、80° B、75° C、40° D、70°

查看试题解析
4. 若三角形三个内角度数比为2：3：4，则这个三角形一定是（　　）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定

查看试题解析
5. 如图，AB＝DB，∠1＝∠2，请问添加下面哪个条件不能判断△ABC≌△DBE的是（）

A、BC＝BE B、∠A＝∠D C、∠ACB＝∠DEB D、AC＝DE

查看试题解析
6. 对于命题“如果∠1+∠2=90°，那么∠1≠∠2”，能说明它是假命题的反例是（）

A、∠1=50°，∠2=40° B、∠1=50°，∠2=50° C、∠1=∠2=45° D、∠1=40°，∠2=40°

查看试题解析
7. 一次函数y＝（m﹣3）x+m+2的图象经过第一、二、四象限，则m的取值范围在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
8. 已知关于x的不等式组 ${\begin{array}{l} x - a > 0 \\ 3 - 2 x > 0 \end{array}$ 的整数解共有5个，则a的取值范围是（）

A、﹣4＜a＜﹣3 B、﹣4≤a＜﹣3 C、a＜﹣3 D、﹣4＜a＜ $\frac{3}{2}$

查看试题解析
9. 如图，在Rt△ABC中，∠ACB＝90°，AC＝5，BC＝12，将△ABC绕点B顺时针旋转60°，得到△BDE，连接DC交AB于点F，则△ACF与△BDF的周长之和为（）

A、44 B、43 C、42 D、41

查看试题解析
10. 如图，在△ABC中，∠ACB＝90°，以△ABC的各边为边分别作正方形BAHI，正方形BCFG与正方形CADE，延长BG，FG分别交AD，DE于点K，J，连结DH，IJ.图中两块阴影部分面积分别记为S₁ ， S₂.若S₁：S₂＝1：4，S_四边形边_BAHE＝18，则四边形MBNJ的面积为（）

A、5 B、6 C、8 D、9

查看试题解析

二、填空题（本大题共8小题，每小题3分，共24分）

11. “内错角相等，两直线平行”的逆命题是．

查看试题解析
12. 若函数y=2x+b（b为常数）的图象经过点A（0，﹣2），则b= ．

查看试题解析
13. 三角形两边长分别是2，4，第三边长为偶数，第三边长为．

查看试题解析
14. 如果点M(a+b，ab)在第二象限，那么点N(a，b)在第象限．

查看试题解析
15. 等腰三角形的一腰上的高与另一腰所在直线的夹角为40°，则这个三角形的底角为．

查看试题解析
16. 如图，Rt△ABC中，∠A＝90°，AB＝3，AC＝4，现将△ABC沿BD进行翻折，使点A刚好落在BC上，则CD＝.

查看试题解析
17. 在直角坐标系中，有A（3，﹣3），B（5，3）两点，现另取一点C（1，n），当△ABC周长最小时，n的值是 .

查看试题解析
18. 如图，在平面直角坐标系中，P是第一象限角平分线上的一点，且P点的横坐标为3．把一块三角板的直角顶点固定在点P处，将此三角板绕点P旋转，在旋转的过程中设一直角边与x轴交于点E，另一直角边与y轴交于点F，若△POE为等腰三角形，则点F的坐标为．

查看试题解析

三、解答题（本大题共6个小题，共46分）

19. 解不等式（组）

(1)、2（5x+3）≤x﹣3（1﹣2x）

(2)、 ${\begin{array}{l} \frac{x - 3}{2} + 3 ⩾ x + 1 \\ 1 - 3 (x - 1) < 8 - x \end{array}$

查看试题解析
20. 如图所示，△ABC在正方形网格中，若点A的坐标为（0，3），按要求回答下列问题：

(1)、在图中建立正确的平面直角坐标系，写出点B和点C的坐标；

(2)、求△ABC的面积．

查看试题解析
21. 如图，等边△ABC的边AC，BC上各有一点E，D，AE＝CD，AD，BE相交于点O.

(1)、求证：△ABE≌△CAD；

(2)、若∠OBD＝45°，求∠ADC的度数.

查看试题解析
22. 校八年级举行英语演讲比赛，购买A，B两种笔记本作为奖品，这两种笔记本的单价分别是12元和8元.根据比赛设奖情况，需购买笔记本共30本，并且所购买A笔记本的数量要不多于B笔记本数量的 $\frac{4}{5}$ ，但又不少于B笔记本数量 $\frac{1}{5}$ ，设买A笔记本n本，买两种笔记本的总费为w元.

(1)、写出w（元）关于n（本）的函数关系式，并求出自变量n的取值范围；

(2)、购买这两种笔记本各多少时，费用最少？最少的费用是多少元？

查看试题解析
23. 定义：若a，b，c是△ABC的三边，且a²+b²＝2c² ，则称△ABC为“方倍三角形”.

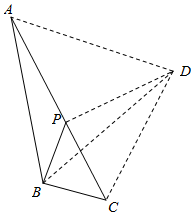(1)、对于①等边三角形②直角三角形，下列说法一定正确的是 .

A、①一定是“方倍三角形” B、②一定是“方倍三角形” C、①②都一定是“方倍三角形” D、①②都一定不是“方倍三角形”

(2)、若Rt△ABC是“方倍三角形”，且斜边AB＝ $\sqrt{3}$ ，则该三角形的面积为；

(3)、如图，△ABC中，∠ABC＝120°，∠ACB＝45°，P为AC边上一点，将△ABP沿直线BP进行折叠，点A落在点D处，连接CD，AD.若△ABD为“方倍三角形”，且AP＝ $\sqrt{2}$ ，求△PDC的面积.

查看试题解析
24. 如图①，已知直线y＝﹣2x+4与x轴、y轴分别交于点A、C，以OA、OC为边在第一象限内作长方形OABC.

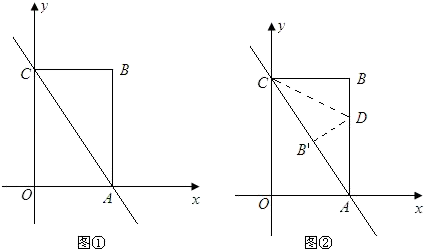(1)、求点A、C的坐标；

(2)、将△ABC对折，使得点A与点C重合，折痕交AB于点D，求直线CD的解析式（图②）；

(3)、在坐标平面内，是否存在点P（除点B外），使得△APC与△ABC全等？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由.

查看试题解析