福建省三明市2022届初中毕业班第一次质量监测数学试卷
试卷更新日期:2022-02-22 类型:中考模拟
一、单选题
-
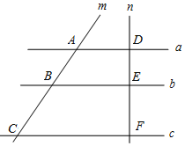
1. 一元二次方程2x2 - 1 = 6x化成一般形式后,常数项是 - 1,一次项系数是( )A、- 2 B、- 6 C、2 D、62. 下列各组图形中,不一定相似的是( )A、任意两个等腰直角三角形 B、任意两个等边三角形 C、任意两个矩形 D、任意两个正方形3. 抛物线 与 轴的交点坐标为( )A、 B、 C、 D、4. 如图,已知直线a∥b∥c,直线m,n与直线a,b,c分别交于点A,B,C,D,E,F,若DE=7,EF=10,则 的值为( )
 A、 B、 C、 D、5. 将二次函数 通过配方可化为 的形式,结果为( )A、 B、 C、 D、6. 如图所示几何体的左视图是( )
A、 B、 C、 D、5. 将二次函数 通过配方可化为 的形式,结果为( )A、 B、 C、 D、6. 如图所示几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 某种芯片实现国产化后,经过两次降价,每块芯片单价由128元降为88元.若两次降价的百分率相同,设每次降价的百分率为x,根据题意,可列方程( )A、128(1 - x2)= 88 B、88(1 + x)2 = 128 C、128(1 - 2x)= 88 D、128(1 - x)2 = 888. 如图,小勇在探究课本“综合与实践”中的“制作视力表”时,根据测试距离为5 m的标准视力表制作了一个测试距离为3 m的视力表.如果标准视力表中“E”的高a是72.7 mm,那么制作出的视力表中相应“E”的高b是( )
7. 某种芯片实现国产化后,经过两次降价,每块芯片单价由128元降为88元.若两次降价的百分率相同,设每次降价的百分率为x,根据题意,可列方程( )A、128(1 - x2)= 88 B、88(1 + x)2 = 128 C、128(1 - 2x)= 88 D、128(1 - x)2 = 888. 如图,小勇在探究课本“综合与实践”中的“制作视力表”时,根据测试距离为5 m的标准视力表制作了一个测试距离为3 m的视力表.如果标准视力表中“E”的高a是72.7 mm,那么制作出的视力表中相应“E”的高b是( ) A、121.17 mm B、43.62 mm C、43.36 mm D、29.08 mm9. 若点A(1,y1),B(2,y2),C(m,y3)在抛物线y= (a≠0)上,且y1<y2<y3 , 则m的值不可能是( )A、5 B、3 C、-3 D、-510. 如图,菱形ABCD中,∠BAD = 60°,AB = 6,点E,F分别在边AB,AD上,将△AEF沿EF翻折得到△GEF,若点G恰好为CD边的中点,则AE的长为( )
A、121.17 mm B、43.62 mm C、43.36 mm D、29.08 mm9. 若点A(1,y1),B(2,y2),C(m,y3)在抛物线y= (a≠0)上,且y1<y2<y3 , 则m的值不可能是( )A、5 B、3 C、-3 D、-510. 如图,菱形ABCD中,∠BAD = 60°,AB = 6,点E,F分别在边AB,AD上,将△AEF沿EF翻折得到△GEF,若点G恰好为CD边的中点,则AE的长为( )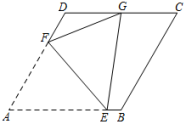 A、 B、 C、 D、3
A、 B、 C、 D、3二、填空题
-
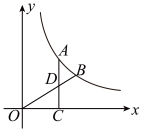
11. 小华在解方程x2 = 3x时,只得出一个根x = 3,则被他漏掉的一个根是x =12. 若 ,则 =.13. 在不透明的袋中装有仅颜色不同的一个红球和一个蓝球,从此袋中随机摸出一个小球,然后放回,再随机摸出一个小球,则两次摸出的球颜色不同的概率是14. 小莉和小林同时站在阳光下,测得身高150 cm的小莉影子长为120 cm,小林的影子比小莉的影子长20 cm,则小林的身高比小莉高cm15. 如图,点A,B为反比例函数 (x>0)图象上的两点,过点A作x轴的垂线,垂足为C,AC与OB交于点D,OD= .若△OCD的面积为2,则k的值为.
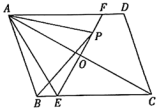
 16. 如图,平行四边形ABCD中,∠ACB = 30°,AC的垂直平分线分别交AC,BC,AD于点O,E,F,点P在OF上,连接AE,PA,PB.若PA = PB,现有以下结论:
16. 如图,平行四边形ABCD中,∠ACB = 30°,AC的垂直平分线分别交AC,BC,AD于点O,E,F,点P在OF上,连接AE,PA,PB.若PA = PB,现有以下结论:①△PAB为等边三角形;
②△PEB∽△APF;
③∠PBC - ∠PAC = 30°;
④EA = EB + EP
其中一定正确的是(写出所有正确结论的序号)
三、解答题
-
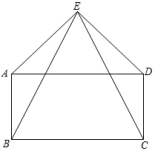
17. 解方程:.18. 如图,点E为矩形ABCD外一点,AE = DE.求证:△ABE≌△DCE
 19. 已知关于x的方程x2 - 5x + m = 0(1)、若方程有一根为 - 1,求m的值;(2)、若方程无实数根,求m的取值范围20. 如图,正方形ABCD的边长为2,点E为AD的中点,点F在BC的延长线上,且∠BEF = 90°;求BF的长
19. 已知关于x的方程x2 - 5x + m = 0(1)、若方程有一根为 - 1,求m的值;(2)、若方程无实数根,求m的取值范围20. 如图,正方形ABCD的边长为2,点E为AD的中点,点F在BC的延长线上,且∠BEF = 90°;求BF的长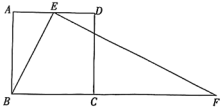 21. 如图,已知△ABC,点D在BC延长线上,且CD = BC
21. 如图,已知△ABC,点D在BC延长线上,且CD = BC (1)、求作平行四边形ACDE;(要求:尺规作图,不写作法,保留作图痕迹);(2)、在(1)的条件下,若F是DE的中点,连接BF交AC于点M,连接CE交BF于点N,求 的值.22. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)与时间x(h)之间的函数关系如图所示,其中BC段是恒温阶段,CD段是某反比例函数图象的一部分,请根据图中信息解答下列问题:
(1)、求作平行四边形ACDE;(要求:尺规作图,不写作法,保留作图痕迹);(2)、在(1)的条件下,若F是DE的中点,连接BF交AC于点M,连接CE交BF于点N,求 的值.22. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)与时间x(h)之间的函数关系如图所示,其中BC段是恒温阶段,CD段是某反比例函数图象的一部分,请根据图中信息解答下列问题: (1)、求a的值;(2)、大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内最适合生长的时间有多长?23. 某智力竞答节目共有10道选择题,每道题有且只有一个选项是正确的;小明已答对前7题,答对最后3题就能顺利通关,其中第8题有A,B两个选项,第9题和第10题都有A,B,C三个选项,假设这3道题小明都不会,只能从所有选项中随机选择一个,不过小明还有两次“求助”没有用(使用一次“求助”可以让主持人在该题的选项中去掉一个错误选项,每道题最多只能使用一次“求助”)(1)、若小明在竞答第8题和第9题时都使用了“求助”,求小明能顺利通关的概率;(2)、从概率的角度分析,如何使用两次“求助”,竞答通关的可能性更大24. 如图①,在Rt△ABC中,∠BAC = 90°,AB = k·AC,△ADE是由△ABC绕点A逆时针旋转某个角度得到的,BC与DE交于点F,直线BD与EC交于点G
(1)、求a的值;(2)、大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内最适合生长的时间有多长?23. 某智力竞答节目共有10道选择题,每道题有且只有一个选项是正确的;小明已答对前7题,答对最后3题就能顺利通关,其中第8题有A,B两个选项,第9题和第10题都有A,B,C三个选项,假设这3道题小明都不会,只能从所有选项中随机选择一个,不过小明还有两次“求助”没有用(使用一次“求助”可以让主持人在该题的选项中去掉一个错误选项,每道题最多只能使用一次“求助”)(1)、若小明在竞答第8题和第9题时都使用了“求助”,求小明能顺利通关的概率;(2)、从概率的角度分析,如何使用两次“求助”,竞答通关的可能性更大24. 如图①,在Rt△ABC中,∠BAC = 90°,AB = k·AC,△ADE是由△ABC绕点A逆时针旋转某个角度得到的,BC与DE交于点F,直线BD与EC交于点G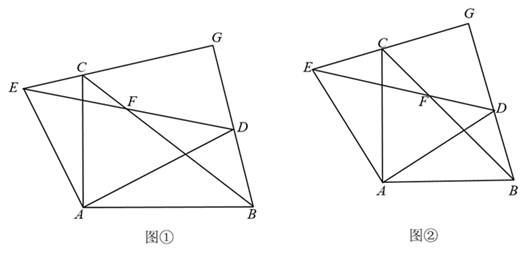 (1)、求证:BD = k·EC;(2)、求∠CGD的度数;(3)、若k = 1(如图②),求证:A,F,G三点在同一直线上.25. 抛物线y = ax2 + bx + c(a≠0)经过点A( - 4,0)和点B(5, )(1)、求证:a + b = ;(2)、若抛物线经过点C(4,0)
(1)、求证:BD = k·EC;(2)、求∠CGD的度数;(3)、若k = 1(如图②),求证:A,F,G三点在同一直线上.25. 抛物线y = ax2 + bx + c(a≠0)经过点A( - 4,0)和点B(5, )(1)、求证:a + b = ;(2)、若抛物线经过点C(4,0)①点D在抛物线上,且点D在第二象限,并满足∠ABD = 2∠BAC,求点D的坐标;
②直线y = kx - 2(k≠0)与抛物线交于M,N两点(点M在点N的左侧),点P是直线MN下方的抛物线上的一点,点Q在y轴上,且四边形MPNQ是平行四边形,求点Q的坐标