福建省泉州市惠安县2021年中考数学质检试卷
试卷更新日期:2022-02-22 类型:中考模拟
一、单选题
-
1. 计算 ,正确结果是( ).A、-6 B、-8 C、6 D、82. 下列运算正确的是( )A、 B、 C、 D、3. 在新冠肺炎防控期间,要了解某学校以下情况,其中适合用普查的有( )
①了解学校口罩、洗手液、消毒片的储备情况;
②了解全体师生在寒假期间的离锡情况;
③了解全体师生入校时的体温情况;
④了解全体师生对“七步洗手法”的运用情况.
A、1个 B、2个 C、3个 D、44. 实数 在数轴上的对应点的位置如图所示,若 ,则下列结论中错误的是( ) A、 B、 C、 D、5. 下图所示的几何体的左视图是( )
A、 B、 C、 D、5. 下图所示的几何体的左视图是( )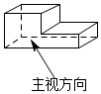 A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,将正方形ABCD沿直线DF折叠,使得点C落在对角线BD上的点 处,则 的度数是( )
6. 如图,将正方形ABCD沿直线DF折叠,使得点C落在对角线BD上的点 处,则 的度数是( ) A、 B、 C、 D、7. 如图,在 中,BD, 分别是 ,AB边上的中线,且BD与CE相交于点C,则 的值为( )
A、 B、 C、 D、7. 如图,在 中,BD, 分别是 ,AB边上的中线,且BD与CE相交于点C,则 的值为( ) A、 B、 C、 D、8. 我国古代《四元玉鉴》中记载“二果问价”问题,其内容如下:九百九十九文钱,甜果苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果几个,又问各该几个钱?其意思为:九百九十九文钱买了甜果和苦果共一千个.已知十一文钱可买九个甜果,四文钱可买七个苦果,那么甜果、苦果各买了多少个?买甜果和苦果各需要多少文钱?若设买甜果x个,买苦果y个,则下列关于 、 的二元一次方程组中符合题意的是( )A、 B、 C、 D、9. 如图,已知 内接于 ,BC是 的直径,AD平分 ,交 于D,若 ,则CD的长为( )
A、 B、 C、 D、8. 我国古代《四元玉鉴》中记载“二果问价”问题,其内容如下:九百九十九文钱,甜果苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果几个,又问各该几个钱?其意思为:九百九十九文钱买了甜果和苦果共一千个.已知十一文钱可买九个甜果,四文钱可买七个苦果,那么甜果、苦果各买了多少个?买甜果和苦果各需要多少文钱?若设买甜果x个,买苦果y个,则下列关于 、 的二元一次方程组中符合题意的是( )A、 B、 C、 D、9. 如图,已知 内接于 ,BC是 的直径,AD平分 ,交 于D,若 ,则CD的长为( ) A、2 B、 C、3 D、10. 已知点 在抛物线 上,当 时,总有 ;当 时,总有 ,则 的值可以是( )A、1 B、-1 C、2 D、-2
A、2 B、 C、3 D、10. 已知点 在抛物线 上,当 时,总有 ;当 时,总有 ,则 的值可以是( )A、1 B、-1 C、2 D、-2二、填空题
-
11. 分解因式: .12. 新华社北京5月11日电11日发布的第七次全国人口普查结果显示,全国人口共141178万人,与2010年第六次全国人口普查数据相比,增加7206万人,增长 ,年平均增长率为0.53%.数据表明,我国人口10年来继续保持低速增长态势.用科学记数法将数据“7206万”表示为 .13. 某家庭记录使用节水龙头50天的日用水量数据(单位: ,得到频数分布表如下:
日用水量
频数
1
5
13
10
16
5
估计该家庭使用节水龙头后,日用水量小于 的概率为.
14. 如图,矩形 的边长 , .把BC绕B逆时针旋转,使C恰好落在AD上的点 处,则 的长是(结果保留 ). 15. 如图,正六边形ABCDEF的面积是 ,则对角线 的长是.
15. 如图,正六边形ABCDEF的面积是 ,则对角线 的长是. 16. 如图,矩形OABC的顶点 , 分别在 轴, 轴正半轴上,反比例函数 的图象分别与矩形OABC两边AB,BC交于点D,E,沿直线DE将 翻折得到 ,且点F恰好落在直线 上.下列四个结论:① ;② ;③ ;④ .其中结论正确的有.(仅填代号即可)
16. 如图,矩形OABC的顶点 , 分别在 轴, 轴正半轴上,反比例函数 的图象分别与矩形OABC两边AB,BC交于点D,E,沿直线DE将 翻折得到 ,且点F恰好落在直线 上.下列四个结论:① ;② ;③ ;④ .其中结论正确的有.(仅填代号即可)
三、解答题
-
17. 解不等式组: ,并把它的解集在数轴上表示出来.18. 如图,在菱形 中,点 、 分别在 、 上,且 .求证: .
 19. 先化简,再求值: ,其中 .20. 某商场按定价销售某种商品时,每件可获利100元;按定价的八折销售该商品5件与将定价降低50元销售该商品6件所获利润相等.(1)、该商品进价、定价分别是多少?(2)、该商场用10000元的总金额购进该商品,并在五一节期间以定价的七折优惠全部售出,在每售出一件该商品时,均捐献 元给社会福利事业,该商场为能获得不低于3000元的利润,求 的最大值.21. 如图,矩形ABCD中,E为AD的中点.
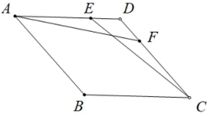
19. 先化简,再求值: ,其中 .20. 某商场按定价销售某种商品时,每件可获利100元;按定价的八折销售该商品5件与将定价降低50元销售该商品6件所获利润相等.(1)、该商品进价、定价分别是多少?(2)、该商场用10000元的总金额购进该商品,并在五一节期间以定价的七折优惠全部售出,在每售出一件该商品时,均捐献 元给社会福利事业,该商场为能获得不低于3000元的利润,求 的最大值.21. 如图,矩形ABCD中,E为AD的中点. (1)、在CD边上求作一点F,使得 ;(2)、在(1)中,若 , ,求BF的长.22. 如图,在 中, , 是边 的延长线上一点, 是边 上一点,且 .
(1)、在CD边上求作一点F,使得 ;(2)、在(1)中,若 , ,求BF的长.22. 如图,在 中, , 是边 的延长线上一点, 是边 上一点,且 . (1)、求证: ;(2)、作 于 点,并连结DE.若 , ,求 的面积.23. 甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下:甲公司规定底薪80元,每销售一件产品提成1元;乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分按每件提成8元.
(1)、求证: ;(2)、作 于 点,并连结DE.若 , ,求 的面积.23. 甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下:甲公司规定底薪80元,每销售一件产品提成1元;乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分按每件提成8元. (1)、分别将甲、乙两家公司一名推销员的日工资y(单位:元)表示为日销售件数 的函数关系式,并写出自变量 的取值范围;(2)、现从甲、乙两家公司各选取一名推销员,随机统计了100天的销售情况,得到如下条形图.若记甲公司推销员的日工资为 元,乙公司推销员的日工资为 元,将该频率视为概率,请回答下面问题:某位大学毕业生拟到甲、乙两家公司应聘产品推销员,如果仅从日均收入高的角度考虑,应选择哪家销售公司?请说明理由.24. 已知四边形 内接于 , .
(1)、分别将甲、乙两家公司一名推销员的日工资y(单位:元)表示为日销售件数 的函数关系式,并写出自变量 的取值范围;(2)、现从甲、乙两家公司各选取一名推销员,随机统计了100天的销售情况,得到如下条形图.若记甲公司推销员的日工资为 元,乙公司推销员的日工资为 元,将该频率视为概率,请回答下面问题:某位大学毕业生拟到甲、乙两家公司应聘产品推销员,如果仅从日均收入高的角度考虑,应选择哪家销售公司?请说明理由.24. 已知四边形 内接于 , . (1)、如图1,求证:点 到 两边的距离相等;(2)、如图2,已知BD与 相交于点E,BD为 的直径.
(1)、如图1,求证:点 到 两边的距离相等;(2)、如图2,已知BD与 相交于点E,BD为 的直径.①求证: ;
②若 , ,求AE的长.
25. 已知抛物线 与 轴交于 和 两点,与 轴交于 点,且 .对于该抛物线上的任意两点 , , , ,当 时,总有 .(1)、求抛物线的解析式;(2)、若过点 的直线 与该抛物线交于另一点E,与线段BC交于点 .作 ,EG与BC交于 点,求 的最大值,并求此时 点的坐标;(3)、若直线 与抛物线交于 , 两点 , 不与 , 重合),直线 , 分别与 轴交于点 , ,设 , 两点的纵坐标分别为 , ,试探究 、 之间的数量关系.