福建省泉州市2021年中考数学最后一卷

试卷更新日期：2022-02-22 类型：中考模拟

进入出卷网下载

一、单选题

1. －6的绝对值是（）

A、-6 B、6 C、- $\frac{1}{6}$ D、 $\frac{1}{6}$

查看试题解析
2. 中俄原油管道于2011年1月11日正式启用，首日输送4.2万吨，年输送1500万吨.年输油量1500万吨用科学记数法表示正确的是（）

A、1.5×10⁷万吨 B、1.5×10³万吨 C、15×10²万吨 D、0.15×10⁴万吨

查看试题解析
3. 下列城市地铁的标志图案中，既是中心对称又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算中，正确的是（）

A、 $a^{3} \cdot a = a^{4}$ B、 ${(a^{3})}^{2} = a^{5}$ C、 $a + a = a^{2}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
5. 如图，下列几何体的俯视图是如图所示图形的是（）

A、 B、 C、 D、

查看试题解析
6. 下列事件属于随机事件的是（）

A、任意画一个三角形，其内角和为180º B、太阳从东方升起 C、掷一次骰子，向上一面点数是7 D、经过有交通信号灯的路口，遇到红灯

查看试题解析
7. 已知a、b在数轴上的位置如图，则 $\sqrt{a^{2}}$ ﹣|b﹣a|的化简结果是（）

A、2a﹣b B、﹣b C、b D、﹣2a+b

查看试题解析
8. 如图，在 $Δ A B C$ 中， $∠ C = 90^{\circ} ， ∠ A = 30^{\circ} ， A B$ 的垂直平分线交 $A C$ 于 $D$ ，交 $A B$ 于 $E ， C D = 2$ ，则 $A C$ 的长为（）

A、 $3$ B、 $4$ C、 $5$ D、 $6$

查看试题解析
9. 如图，若AB是 $⊙ O$ 的直径，CD是 $⊙ O$ 的弦， $∠ A B D = 58 °$ ，则 $∠ C$ 的度数为（）

A、116° B、58° C、42° D、32°

查看试题解析
10. 已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与 $x$ 轴交于点 $A (- 1 ， 0)$ ，对称轴为 $x = 1$ ，与 $y$ 轴的交点 $B$ 在 $(0 ， 2)$ 和 $(0 ， 3)$ 之间（包含这两个点）运动.有如下四个结论：①抛物线与 $x$ 轴的另一个交点是 $(3 ， 0)$ ；②点 $C (x_{1}$ ， $y_{1})$ ， $D (x_{2}$ ， $y_{2})$ 在抛物线上，且满足 $x_{1} < x_{2} < 1$ ，则 $y_{1} > y_{2}$ ；③常数项 $c$ 的取值范围是 $2 ⩽ c ⩽ 3$ ；④系数 $a$ 的取值范围是 $- 1 ⩽ a ⩽ - \frac{2}{3}$ .上述结论中，所有正确结论的序号是（）

A、①②③ B、②③④ C、①④ D、①③④

查看试题解析

二、填空题

11. 现定义一种新的运算： $a * b = a^{2} - 2 b$ .例如 $3 * 4 = 3^{2} - 2 \times 4 = 1$ ，则不等式 $(- 4) * x \geq 0$ 的解集为.

查看试题解析
12. 如果一个正多边形的内角和等于 $1440 °$ ，那么这个正多边形的每一个外角的度数为.

查看试题解析
13. 某电脑公司销售部为了制订下个月的销售计划，对20位销售员本月的销售量进行了统计，绘制成如图所示的统计图，则这20位销售员本月销售量的平均数、中位数、众数分别是.

查看试题解析
14. 已知 $m - n = 3$ ，则 $m^{2} - n^{2} - 6 n$ 的值

查看试题解析
15. 如图所示的图案是我国汉代数学家赵爽在注解《周髀算经》中“赵爽弦图”经修饰后的图形，四边形 $A B C D$ 与四边形 $E F G H$ 均为正方形，点H是 $D E$ 的中点，阴影部分的面积为24，则 $A D$ 的长为..

查看试题解析
16. 如图，点A、C为反比例函数 $y_{1} = - \frac{6}{x}$ 上的动点，点B、D为反比例函数 $y_{2} = \frac{2}{x}$ 上的动点，若四边形 $A B C D$ 为菱形，则该菱形边长的最小值为.

查看试题解析

三、解答题

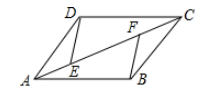
17. 解方程组： ${\begin{array}{l} x + 2 y = 5 ① \\ 3 x - 2 y = - 1 ② \end{array}$

查看试题解析
18. 先化简，再求值： $(\frac{2 x - 4}{x^{2} - 4 x + 4} - \frac{x + 2}{x^{2} - 2 x}) \div \frac{x - 1}{x}$ ，其中 $x = \sqrt{2}$

查看试题解析
19. 如图，点E，F分别是 $▱$ $A B C D$ 对角线AC上两点， $A F = C E$ .求证： $∠ D E C = ∠ B F A$ .

查看试题解析
20. 如图 1，已知 AB∥CD，BE 平分∠ABD，DE 平分∠BDC.（∠ABD 的度数大于 90° 小于 120°）

(1)、求证：∠BED = 90°；

(2)、若点 F 为射线 BE 上一点，∠EDF = α，∠ABF 的角平分线 BG 与∠CDF 的角平分线DG 交于点 G，试用含α的式子表示∠BGD 的大小；

(3)、延长BE交CD于点H，点F为线段 BH 上一动点，∠ABF 邻补角的角平分线与∠CDF邻补角的角平分线 DG 交于点 G，探究∠BGD 与∠BFD 之间的数量关系，请直接写出结论：.（题中所有的角都是大于 0°小于 180°的角）

查看试题解析
21. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 8$ ， $B C = 6$ ，将 $△ A B C$ 绕点B按顺时针方向旋转得到 $△ D B E$ ，当点E恰好落在线段 $A B$ 上时，连接 $A D$ ， $∠ A B D$ 的平分线 $B F$ 交 $A D$ 于点F，连接 $E F$ .

(1)、求 $E F$ 的长；

(2)、求证：C、E、F三点共线.

查看试题解析
22. 小明家今年种植的“红灯”樱桃喜获丰收，采摘上市20天全部销售完，小明对销售情况进行跟踪记录，并将记录情况绘成图象，日销售量y（单位：千克）与上市时间x（单位：天）的函数关系如图1所示，樱桃价格z（单位：元/千克）与上市时间x（单位：天）的函数关系式如图2所示.

(1)、观察图象，直接写出日销售量的最大值；

(2)、求小明家樱桃的日销售量y与上市时间x的函数解析式；

(3)、试比较第10天与第12天的销售金额哪天多？

查看试题解析
23. 某市教育局为了了解初二学生每学期参加综合实践活动的情况，随机抽样调查了某校初二学生一个学期参加综合实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图.请你根据图中提供的信息，回答下列问题：

(1)、扇形统计图中a的值为；

(2)、补全频数分布直方图；

(3)、在这次抽样调查中，众数是天，中位数是天；

(4)、请你估计该市初二学生每学期参加综合实践活动的平均天数约是多少？（结果保留整数）

查看试题解析
24. 如图1，在直角坐标系xOy中，直线l与x、y轴分别交于点A（4，0）、B（0， $\frac{16}{3}$ ）两点，∠BAO的角平分线交y轴于点D．点C为直线l上一点，以AC为直径的⊙G经过点D，且与x轴交于另一点E．

(1)、求证：y轴是⊙G的切线；

(2)、请求⊙G的半径r，并直接写出点C的坐标；

(3)、如图2，若点F为⊙G上的一点，连接AF，且满足∠FEA=45°，请求出EF的长？

查看试题解析
25. 已知顶点为D的抛物线 $y = a {(x - 3)}^{2} (a \neq 0)$ 交y轴于点 $C (0 ， 3)$ ，且与直线l交于不同的两点A、B（A、B不与点D重合）.

(1)、求抛物线的解析式；

(2)、若 $∠ A D B = 90 °$ ，
①试说明：直线l必过定点；

②过点D作 $D F ⊥ l$ ，垂足为点F，求点C到点F的最短距离.

查看试题解析