福建省福州十九中2021年中考数学三模试卷
试卷更新日期:2022-02-22 类型:中考模拟
一、单选题
-
1. 2021的倒数是( )A、 B、﹣ C、﹣2021 D、2021
-
2. 如图所示的几何体是由两个圆柱体和一个正方体组成,圆柱体的直径和高均与正方体的棱长相等,则其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
3. 自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识.下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
4. 在凸n边形中,小于108°的角最多可以有( )A、3个 B、4个 C、5个 D、6个
-
5. 下列运算正确的是( )A、a0=0 B、a3+a2=a5 C、a2•a﹣1=a D、
-
6. 如图,AC∥EF∥DB,若AC=8,BD=12,则EF=( )
 A、3 B、 C、4 D、
A、3 B、 C、4 D、 -
7. 一组数据: ,a,a, ,若添加一个数据a,下列说法错误的是A、平均数不变 B、中位数不变 C、众数不变 D、方差不变
-
8. 若关于x的一元二次方程ax2+bx+c=0的两根中只有一个为0,则下列说法正确的是( )A、b≠0,c≠0 B、b=0,c≠0 C、b≠0,c=0 D、b=0,c=0
-
9. 如图,在Rt△ABC中,∠ABC=90°,AB= ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
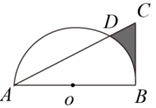 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点横坐标为﹣2,x0 , 且满足(a+b+c)(4a+2b+c)<0,与y轴的负半轴相交,抛物线经过点A(﹣1,y1),B(﹣ ,y2),C(1,y3),正确结论是( )A、y3>y2>y1 B、y3>y1>y2 C、y1>y2>y3 D、y1>y3>y2
二、填空题
-
11. 分解因式:a2+2a= .
-
12. 一个暗箱中放有除颜色外其他完全相同的n个红球,18个黄球,9个白球,现将球搅匀后,任意摸出1个球记下颜色,再放回暗箱,通过大量重复试验后发现,摸到黄球的频率稳定在30%附近,由此可以估算的n值是 .
-
13. 已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为 ,则该扇形的面积是.
-
14. 当 与 时,代数式 的值相等,则 时,代数式 的值为.
-
15. 如图,边长为1的小正方形网格中,点A、B、C、E在格点上,连接AE、BC,点D在BC上,且满足AD⊥BC,则∠AED的正切值是.

-
16. 如图,点A,B,C在反比例函数y=﹣ 的图象上,且直线AB经过原点,点C在第二象限上,连接AC并延长交x轴于点D,连接BD,若△BOD的面积为12,AC=kCD,则 =.

三、解答题
-
17. 解不等式组 ,并把解集在数轴上表示出来:
-
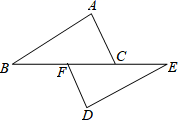
18. 如图:△ABC与△DEF中,边BC,EF在同一条直线上,AB∥DE,AC∥DF,且BF=CE,求证:AC=DF.
-
19. 先化简,再求值: ,其中x=1﹣ .
-
20. 小宝大学毕业后回家乡进行园艺创业,第一期培植盆景与花卉各50盆,售后进行统计得知:盆景的平均每盆利润是160元,花卉的平均每盆利润是20元.调研发现:①盆景每增加1盆,盆景的平均每盆利润减少2元:每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变,小宝计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1、W2(单位:元)(1)、用含x的代数式分别表示W1、W2;(2)、当x取何值时,第二期培植的盆景与花卉销售完所获得的总利润最大?最大总利润是多少?
-
21. 某路段上有A、B两处相距近200m且未设红绿灯的斑马线,为使交通高峰期该路段车辆与行人的通行更有序,交通部门打算在汽车平均停留时间较长的一处斑马线上放置移动红绿灯.图1,图2分别是交通高峰期来往车辆在A、B斑马线前停留时间的抽样统计图

根据统计图解决下列问题:
(1)、若某日交通高峰期共有450辆车经过A斑马线,请估计其中停留时间为10s~12s的车辆数为辆,这些停留时间为10s~12s的车辆的平均停留时间为s;(2)、移动红绿灯放置在哪一处斑马线上较为合适?请说明理由. -
22.(1)、尺规作图:如图, 、 是平面上两个定点,在平面上找一点 ,使 构成等腰直角三角形,且 为直角顶点.(画出一个点 即可)
 (2)、在(1)的条件下,若 , ,则点 的坐标是.
(2)、在(1)的条件下,若 , ,则点 的坐标是. -
23. 如图1,AB为半圆的直径,点O为圆心,AF为半圆的切线,过半圆上的点C作CD∥AB交AF于点D,连接BC.
 (1)、连接DO,若BC∥OD,求证:CD是半圆的切线;(2)、如图2,当线段CD与半圆交于点E时,连接AE,AC,判断∠AED和∠ACD的数量关系,并证明你的结论.
(1)、连接DO,若BC∥OD,求证:CD是半圆的切线;(2)、如图2,当线段CD与半圆交于点E时,连接AE,AC,判断∠AED和∠ACD的数量关系,并证明你的结论. -
24. 如图1,在正方形ABCD中,边长为2a,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B作BF⊥CE于点G,交AD于点F.
 (1)、求证:AF=BE;(2)、如图2,当点E运动到AB中点时,连接DG,求证:DG=2a;(3)、如图3,在(2)的条件下,过点C作CM⊥DG于点H,分别交AD,BF于点M,N,求 的值.
(1)、求证:AF=BE;(2)、如图2,当点E运动到AB中点时,连接DG,求证:DG=2a;(3)、如图3,在(2)的条件下,过点C作CM⊥DG于点H,分别交AD,BF于点M,N,求 的值. -
25. 如图1,已知抛物线y=﹣x2﹣2x+c与x轴交于A,B两点,且AB=4.
 (1)、求c的值及抛物线顶点C的坐标;(2)、设点D是x轴上一点,当cos(∠CAO+∠CDO)= 时,求点D的坐标;(3)、如图2,抛物线与y轴交于点E,点P是该抛物线上位于第二象限的点,线段PA交BE于点M,交y轴于点N,设△ABP和△AEN的面积分别为m、n,求m+n的最大值.
(1)、求c的值及抛物线顶点C的坐标;(2)、设点D是x轴上一点,当cos(∠CAO+∠CDO)= 时,求点D的坐标;(3)、如图2,抛物线与y轴交于点E,点P是该抛物线上位于第二象限的点,线段PA交BE于点M,交y轴于点N,设△ABP和△AEN的面积分别为m、n,求m+n的最大值.
