2022届南京中考数学中考一模仿真试题

试卷更新日期：2022-02-21 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，在数轴上，实数a，b的对应点分别为点 $A ， B$ ，则 $a b =$ （）

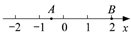A、1.5 B、1 C、-1 D、-4

查看试题解析
2. 若 $| m - n | = n - m$ ，且 $\sqrt{m^{2}} = 4$ ， $\sqrt{n^{2}}$ =3，则 $\sqrt{{(m + n)}^{2}}$ 的值是（）

A、-1 B、7 C、1或7 D、-1或-7

查看试题解析
3. 二十四节气是中国古代劳动人民长期经验积累的结品，它与白昼时长密切相关．当春分、秋分时，昼夜时长大致相等；当夏至时，白昼时长最长．下图是一年中部分节气所对应的白昼时长示意图．在下列选项中白昼时长超过14小时的节气是（）

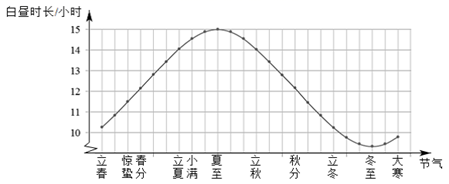A、惊蛰 B、立夏 C、夏至 D、大寒

查看试题解析
4. 下列说法正确的是（）

A、一组数据2，2，3，4的众数是2，中位数是2.5 B、了解某市市民知晓“礼让行人”交通新规的情况，适合全面调查 C、甲、乙两人跳远成绩的方差分别为 $s^{2}$ _{甲 $= 3$} ， $s^{2}$ _乙 $= 4$ ，说明乙的跳远成绩比甲稳定 D、可能性是1%的事件在一次试验中一定不会发生

查看试题解析
5. 如图，正方形 $A B C D$ 的对角线 $B D$ 长为 $2 \sqrt{2}$ ，若直线 $l$ 满足：①点 $D$ 到直线 $l$ 的距离为 $\sqrt{3}$ ；② $A ， C$ 两点到直线 $l$ 的距离相等，则正确的直线 $l$ 的条数为（）

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，在等腰三角形△ABC中，O为底边BC的中点，以O为圆心作半圆与AB，AC相切，切点分别为D，E.过半圆上一点F作半圆的切线，分别交AB，AC于M，N.那么 $\frac{B M \cdot C N}{B C^{2}}$ 的值等于（）

A、 $\frac{1}{8}$ B、 $\frac{1}{4}$ C、 $\frac{1}{2}$ D、1

查看试题解析

二、填空题

7. 当x时， $\frac{\sqrt{x + 1}}{x - 2}$ 在实数范围内有意义.

查看试题解析
8. 据日本环境省估计，被2011年地震海啸吞没然后流入太平洋的废墟垃圾共约5000000吨，其中5000000吨用科学记数法表示为吨．

查看试题解析
9. 分解因式：x（x﹣2）+1=.

查看试题解析
10. 已知 $\frac{m + n}{n} = \frac{8}{15}$ ，则 $\frac{n}{m}$ ＝．

查看试题解析
11. 若关于 $x$ 的一元二次方程 $3 x^{2} - 2 x + m = 0$ 有两个相等的实数根；则 $m$ 的值为．

查看试题解析
12. 《算法统宗》是中国古代数学名著，作者是明代数学家程大位．其中有一个“绳索量竿”问题：“一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托，问索长几尺”．
译文：现有一根杆和一条绳索，用绳索去量杄，绳索比杆子长5尺；如果将绳索对折后再去量竿，就比竿子短5尺，问绳索长几尺？注：一托 $= 5$ 尺

设绳索长X尺，竿子长y尺，依题意，可列方程组为．

查看试题解析
13. 如图，点 $F$ 在正五边形 $A B C D E$ 的边 $C D$ 的延长线上，连接 $A D$ ，则 $∠ A D F =$ .

查看试题解析
14. 如图，直线 $y = m x - 1$ 交 $y$ 轴于点B，交 $x$ 轴于点C，以BC为边的正方形ABCD的顶点A（-1，a）在双曲线 $y = - \frac{2}{x} (x < 0)$ 上，D点在双曲线 $y = \frac{k}{x} (x > 0)$ 上，则 $k$ 的值为.

查看试题解析
15. 如图，已知正方形ABCD的边长为4，点E是正方形内部一点，连接BE、CE，且∠ABE＝∠BCE，点P是AB边上一动点，连接PD、PE，则PD＋PE的最小值为 .

查看试题解析
16. 如图，在平面直角坐标系中，线段AB的两个端点的坐标分别为（-1，2）、（1，1）．抛物线y=ax²+bx+c（a≠0）与x轴交于C、D两点，点C在点D左侧，当顶点在线段AB上移动时，点C横坐标的最小值为-2．在抛物线移动过程中，a-b+c的最小值是．

查看试题解析

三、解答题

17. 解不等式组： ${\begin{array}{l} 3 - 2 x \leq x + 11 \\ \frac{2 x + 5}{3} - 1 < 2 - x \end{array}$

查看试题解析
18. 化简求值：（ $\frac{5}{x - 3}$ ＋x＋3）÷ $\frac{2 x - 4}{x - 3}$ ，其中x＝5

查看试题解析
19. 已知 $x^{2} + x - 1 = 0$ ，求代数式 $(x + 1) (x - 1) + x (x + 2)$ 的值．

查看试题解析
20. 如图，在正方形ABCD中，点E、F、G 分别在AB、BC、CD上，且 $E F ⊥ F G$ 于F．

(1)、求证：△BEF∽△CFG；

(2)、若AB=12，AE=3，CF=4，求CG的长．

查看试题解析

21. 今年春季开学后，为了庆祝伟大的中国共产党建党100周年，某校开展了“爱祖国•跟党走”的知识网上答题竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，共分成四组：

A.80≤x＜85，B.85≤x＜90，C.90≤x＜95，D.95≤x≤100）

下面给出了部分信息：

七年级10名学生的竞赛成绩是：90，81，90，86，99，95，96，100，89，84

八年级10名学生的竞赛成绩在C组中的数据是：90，94，94

七，八年级抽取的学生竞赛成绩统计表

年级	七年级	八年级
平均数	91	91
中位数	90	b
众数	c	100
方差	52	50.4

根据以上信息，解答下列问题：

(1)、直接写出上述图表中a、b、c的值；

(2)、根据以上数据，你认为该校七、八年级中哪个年级学生掌握的相关知识较好？请说明理由（一条理由即可）；

(3)、该校七、八年级各600人参加了此次网上答题竞赛活动，估计参加竞赛活动成绩优秀（x≥90）的学生人数是多少？

查看试题解析

22. 有六张完全相同的卡片，分 $A ， B$ 两组，每组三张，在 $A$ 组的卡片上分别画上“√，×，√”， $B$ 组的卡片上分别画上“√，×，×”，如图①所示．

(1)、若将卡片无标记的一面朝上摆在桌上，再分别从两组卡片中随机各抽取一张，求两张卡片上标记都是“√”的概率（请用“树形图法”或“列表法”求解）．

(2)、若把 $A ， B$ 两组卡片无标记的一面对应粘贴在一起得到三张卡片，其正、反面标记如图②所示，将卡片正面朝上摆在桌上，并用瓶盖盖住标记．
①若随机揭开其中一个盖子，看到的标记是“√”的概率是多少？

②若揭开盖子，看到的卡片正面标记是“√”后，猜想它的反面也是“√”，求猜对的概率．

查看试题解析
23. 为了主题为“醉美遵义酒都仁怀”第十三届遵义文化旅游产业发展大会召开，仁怀某社区计划对面积为 $2000 m^{2}$ 的区域进行绿化，经投标，由甲、乙两个工程队来完成，已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2.5倍，并且在独立完成面积为 $500 m^{2}$ 区域的绿化时，甲队比乙队少用6天.

(1)、求甲、乙两工程队每天能完成绿化的面积.

(2)、设甲工程队施工 $x$ 天，乙工程队施工 $y$ 天刚好完成绿化任务，求 $y$ 与 $x$ 的函数解析式.

(3)、若甲队每天绿化费用是1.5万元，乙队每天绿化费用为0.5万元，且甲乙两队施工的总天数不超过19天，则如何安排甲、乙两队施工的天数，使施工总费用最低？并求出最低费用.

查看试题解析

24. 蔡明园公园位于河南省驻马店市上蔡县蔡都镇西南部，其公园南山门被誉为“亚洲第一门”，学完了三角函数知识后，某数学“综合与实践”小组的同学把“测量南山门最高点的高度”作为一项课题活动，他们制定了测量方案，并利用课余时间完成了实地测量.为了减小测量误差，小组在测量仰角以及两点间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如表：

课题	测量南山门最高点的高度
实物图
成员	组长：xxx 组员：xxx，xxx，xxx
测量工具	卷尺、测角仪……
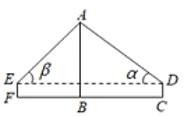
测量示意图				说明：AB表示南山门最高点到地面的竖直距离.测角仪的高度CD-EF-1.5m点C.F与点B在同一直线上，点C.F之间的距离可直接测将，且点A、B.C.D.E、F在同一平面内.
测量数据	第一次	第二次	平均值
	35.95°	36.05°	36°
	45.09°	44.91°	45°
	79.58m	79.62m	79.6m
……	……

(1)、请帮助该小组的同学根据上表中的测量数据，求南山门最高点的高度AB.（结果精确到0.1m，参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73，

\sqrt{2}

≈1.41）

(2)、该小组要写出一份完整的课题活动报告，除上表中的项目外，你认为还需要补充哪些项目？（写出一个即可）（如需作图或作辅助线，请先将原题草图画在对应题目的答题区域后再作答.）

查看试题解析

25. 悬索桥，又名吊桥，指的是以通过索塔悬挂并锚固于两岸（或桥两端）的缆索（或钢链）作为上部结构主要承重构件的桥梁. 其缆索几何形状一般近似于抛物线.从缆索垂下许多吊杆（吊杆垂直于桥面），把桥面吊住.某悬索桥（如图1），是连接两个地区的重要通道. 图2是该悬索桥的示意图.小明在游览该大桥时，被这座雄伟壮观的大桥所吸引. 他通过查找资料了解到此桥的相关信息：这座桥的缆索（即图2中桥上方的曲线）的形状近似于抛物线，两端的索塔在桥面以上部分高度相同，即AB=CD，两个索塔均与桥面垂直. 主桥AC的长为600 m，引桥CE的长为124 m.缆索最低处的吊杆MN长为3 m，桥面上与点M相距100 m处的吊杆PQ长为13 m.若将缆索的形状视为抛物线，请你根据小明获得的信息，建立适当的平面直角坐标系，求出索塔顶端D与锚点E的距离.

图2

查看试题解析
26. 如图，点 $C$ 是以 $A B$ 为直径的 $⊙ O$ 上一点，过点 $A$ 作 $⊙ O$ 的切线交 $B C$ 延长线于点 $D$ ，取 $A D$ 中点 $E$ ，连接 $E C$ 并延长交 $A B$ 延长线于点 $F$ .

(1)、试判断 $E F$ 与 $⊙ O$ 的位置关系，并说明理由；

(2)、若 $C F = 12$ ， $B F = 8$ ，求 $\tan D$ .

查看试题解析
27. 小明将两个直角三角形纸片如图（1）那样拼放在同一平面上，抽象出如图（2）的平面图形， $∠ A C B$ 与 $∠ E C D$ 恰好为对顶角， $∠ A B C = ∠ C D E = 90 °$ ，连接 $B D$ ， $A B = B D$ ，点F是线段 $C E$ 上一点．

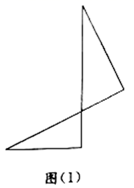
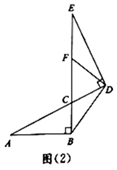
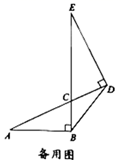(1)、探究发现：
当点F为线段 $C E$ 的中点时，连接 $D F$ （如图（2），小明经过探究，得到结论： $B D ⊥ D F$ ．你认为此结论是否成立？．（填“是”或“否”）

(2)、拓展延伸：
将（1）中的条件与结论互换，即：若 $B D ⊥ D F$ ，则点F为线段 $C E$ 的中点．请判断此结论是否成立．若成立，请写出证明过程；若不成立，请说明理由．

(3)、问题解决：
若 $A B = 6 ， C E = 9$ ，求 $A D$ 的长．

查看试题解析