人教版初中数学七年级下册第五章 相交线与平行线 单元测试
试卷更新日期:2022-02-21 类型:单元试卷
一、单选题
-
1.
下列五幅图案中,⑵、⑶、⑷、⑸中的哪个图案可以由(1)图案平移得到?( )
 A、⑵; B、⑶; C、⑷; D、⑸.2. 下列图形中线段PQ的长度表示点P到直线a的距离的是( )A、
A、⑵; B、⑶; C、⑷; D、⑸.2. 下列图形中线段PQ的长度表示点P到直线a的距离的是( )A、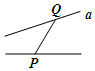 B、
B、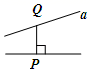 C、
C、 D、
D、 3. 如图所示,直线a∥b.AC⊥AB.AC交直线b于点C.∠1=65°.则∠2的度数是( )
3. 如图所示,直线a∥b.AC⊥AB.AC交直线b于点C.∠1=65°.则∠2的度数是( )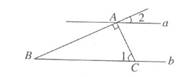 A、65° B、50° C、35° D、25°4. 下列命题中,是真命题的是( )A、过一点有且只有一条直线与已知直线平行 B、平移的方向一定是水平的 C、同旁内角互补 D、对顶角相等5. 直线AB∥CD , ∠B=23°,∠D=42°,则∠E=( )
A、65° B、50° C、35° D、25°4. 下列命题中,是真命题的是( )A、过一点有且只有一条直线与已知直线平行 B、平移的方向一定是水平的 C、同旁内角互补 D、对顶角相等5. 直线AB∥CD , ∠B=23°,∠D=42°,则∠E=( ) A、23° B、42° C、65° D、19°6. 如图,下列条件中能判定直线l1∥l2的是( )
A、23° B、42° C、65° D、19°6. 如图,下列条件中能判定直线l1∥l2的是( )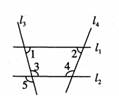 A、∠1=∠2 B、∠1+∠3= 180° C、∠4=∠5 D、∠3=∠57. 如图,由已知条件推出结论正确的是( )
A、∠1=∠2 B、∠1+∠3= 180° C、∠4=∠5 D、∠3=∠57. 如图,由已知条件推出结论正确的是( )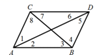 A、由 ,可以推出 B、由 ,可以推出 C、由 ,可以推出 D、由 ,可以推出8. 如图.将矩形直尺的一个顶点与三角尺的直角顶点重合放置,测得∠1=25°,则∠2的度数为( )
A、由 ,可以推出 B、由 ,可以推出 C、由 ,可以推出 D、由 ,可以推出8. 如图.将矩形直尺的一个顶点与三角尺的直角顶点重合放置,测得∠1=25°,则∠2的度数为( ) A、15° B、35 C、45° D、65°9. 如图,下列条件:(1)∠1=∠3;(2)∠2=∠4;(3)∠6=∠8;(4)∠2+∠3=180°,其中能判定 a∥b 的有( )
A、15° B、35 C、45° D、65°9. 如图,下列条件:(1)∠1=∠3;(2)∠2=∠4;(3)∠6=∠8;(4)∠2+∠3=180°,其中能判定 a∥b 的有( ) A、1 个 B、2 个 C、3 个 D、4 个10. 学习平行线后,张明想出了过已知直线外一点画这条直线的平行线的新方法,他是通过折一张半透明的纸得到的.观察图(1)~(4),经两次折叠展开后折痕CD所在的直线即为过点P与已知直线a平行的直线.由操作过程可知张明画平行线的依据有( )
A、1 个 B、2 个 C、3 个 D、4 个10. 学习平行线后,张明想出了过已知直线外一点画这条直线的平行线的新方法,他是通过折一张半透明的纸得到的.观察图(1)~(4),经两次折叠展开后折痕CD所在的直线即为过点P与已知直线a平行的直线.由操作过程可知张明画平行线的依据有( )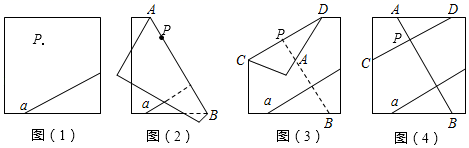
①同位角相等,两直线平行;
②两直线平行,同位角相等;
③内错角相等,两直线平行;
④同旁内角互补,两直线平行.
A、①③ B、①②③ C、③④ D、①③④二、填空题
-
11. 如图所示,想在河堤两岸塔建一座桥,搭建方式最短的是 , 理由 .
 12. 如图, , ,则图中与 相等的角( 除外)共有个.
12. 如图, , ,则图中与 相等的角( 除外)共有个. 13. 如图,一块直角三角板的两锐角的顶点刚好落在平行线 上,已知 是直角,则 的度数等于 .
13. 如图,一块直角三角板的两锐角的顶点刚好落在平行线 上,已知 是直角,则 的度数等于 . 14. 如图, , , ,则 度.
14. 如图, , , ,则 度. 15. 直线a、b、c、d以如图所示的方式相交,且 和 互为余角, 是 的余角的补角, ,则 .
15. 直线a、b、c、d以如图所示的方式相交,且 和 互为余角, 是 的余角的补角, ,则 .
三、解答题
-
16. 请把以下说理过程补充完整:
如图,AB∥CD,∠C=∠D,如果∠1=∠2,那么∠E与∠C
互为补角吗?说说你的理由.
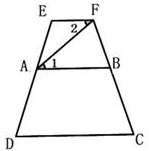
解:因为∠1=∠2,
根据 ▲ ,
所以EF∥ ▲ .
又因为AB∥CD,
根据 ▲ ,
所以EF∥ ▲ .
根据 ▲ ,
所以∠E+ ▲ = ▲ °.
又因为∠C=∠D,
所以∠E+ ▲ = ▲ °,
所以∠E与∠C互为补角.
17. 如图,点 , , 分别是三角形 的边 , , 上的点, , .求证: . 18. 将一副直角三角板如图放置,已知AE∥BC,求∠AFD的度数.
18. 将一副直角三角板如图放置,已知AE∥BC,求∠AFD的度数. 19.
19.如图,已知点E,F分别在BA,CD的延长线上,连接EF,交AC,BD于G,H点,且∠1=∠2,∠B=∠C.
(1)AC与BD平行吗?为什么?
(2)BE与CF平行吗?为什么?
 20.
20.已知如图,CD⊥AB于点D,EF⊥AB于点F,∠1=∠2.
(1)求证:CD∥EF;
(2)判断∠ADG与∠B的数量关系?如果相等,请说明理由;如果不相等,也请说明理由.

四、综合题
-
21. 已知:三角形ABC和三角形DEF位于直线MN的两侧中,直线MN经过点C , 且 ,其中 , , ,点E、F均落在直线MN上.
 (1)、如图1,当点C与点E重合时,求证: ;聪明的小丽过点C作 ,并利用这条辅助线解决了问题.请你根据小丽的思考,写出解决这一问题的过程.(2)、将三角形DEF沿着NM的方向平移,如图2,求证: ;(3)、将三角形DEF沿着NM的方向平移,使得点E移动到点 ,画出平移后的三角形DEF , 并回答问题,若 ,则 . (用含 的代数式表示)
(1)、如图1,当点C与点E重合时,求证: ;聪明的小丽过点C作 ,并利用这条辅助线解决了问题.请你根据小丽的思考,写出解决这一问题的过程.(2)、将三角形DEF沿着NM的方向平移,如图2,求证: ;(3)、将三角形DEF沿着NM的方向平移,使得点E移动到点 ,画出平移后的三角形DEF , 并回答问题,若 ,则 . (用含 的代数式表示)