广东省茂名市2022届高三数学一模试卷

试卷更新日期：2022-02-21 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合A={x|-1 $\leq$ 3}，B={-1，0，2，3}，则A∩B=（）

A、 ${- 1 ， 0 ， 2 ， 3}$ B、 ${0 ， 3}$ C、 ${0 ， 2}$ D、 ${0 ， 2 ， 3}$

查看试题解析
2. 已知 $a ， b$ 为实数，且 $\frac{2 + b i}{1 + i} = a + i$ （ $i$ 为虚数单位），则 $a + b i =$ （）

A、 $3 + 4 i$ B、 $1 + 2 i$ C、 $- 3 - 2 i$ D、 $3 + 2 i$

查看试题解析
3. 下面四个命题中，其中正确的命题是（）
$p_{1}$ ：如果两个平行平面同时和第三个平面相交，那么它们的交线平行
$p_{2}$ ：两个平面垂直，如果有一条直线垂直于这两个平面的交线，那么这条直线与其中一个平面垂直
$p_{3}$ ：一条直线与一个平面平行，如果过该直线的平面与此平面相交，那该直线与交线平行
$p_{4}$ ：一条直线与一个平面内的一条直线平行，则这条直线就与这个平面平行

A、 $p_{1}$ 与 $p_{2}$ B、 $p_{2}$ 与 $p_{3}$ C、 $p_{3}$ 与 $p_{4}$ D、 $p_{1}$ 与 $p_{3}$

查看试题解析
4. 已知角 $α$ 的顶点在原点，始边与 $x$ 轴非负半轴重合，终边与直线 $2 x + y + 3 = 0$ 平行，则 $\frac{s i n α - c o s α}{s i n α + c o s α}$ 的值为（）

A、-2 B、 $- \frac{1}{4}$ C、2 D、3

查看试题解析
5. 已知等比数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，公比为 $q$ ，则下列选项正确的是（）

A、若 $S_{3} = 4 ， S_{6} = 12$ ，则 $S_{9} = 29$ B、若 $a_{1} = 1 ， q = \frac{3}{4}$ ，则 $S_{n} = 4 - 3 a_{n}$ C、若 $a_{4} + a_{7} = 2 ， a_{5} a_{6} = - 8$ ，则 $a_{1} + a_{10} = - 6$ D、若 $a_{1} = 1 ， a_{5} = 4 a_{3}$ ，则 $a_{n} = 2^{n - 1}$

查看试题解析
6. 已知 $x ， y ， z$ 均为大于0的实数，且 $2^{x} = 3^{y} = l o g_{5} z$ ，则 $x ， y ， z$ 大小关系正确的是（）

A、 $x > y > z$ B、 $x > z > y$ C、 $z > x > y$ D、 $z > y > x$

查看试题解析
7. 过三点A（0，0），B（0，2），C（2，0）的圆M与直线 $l ： k x - y + 2 - 2 k = 0$ 的位置关系是（）

A、相交 B、相切 C、相交或相切 D、相切或相离

查看试题解析
8. 已知 $f (x) = s i n x$ ， $g (x) = l n | x | + (e x)^{2}$ ，则 $f (x) \cdot g (x) > 0$ 的解集是（）

A、 ${x | - \frac{1}{e} < x < 0$ 或 $\frac{1}{e} < x < π$ 或 $2 n π < x < (2 n + 1) π ， n \in Z ，$ 且 $n \neq 0$ $}$ B、 ${x | - π < x < - \frac{1}{e}$ 或 $\frac{1}{e} < x < π$ 或 $2 n π < x < (2 n + 1) π ， n \in Z$ ，且 $n \neq 0}$ C、 ${x | - \frac{1}{e} < x < 0$ 或 $0 < x < \frac{1}{e}$ 或 $2 n π < x < (2 n + 1) π ， n \in Z ，$ 且 $n \neq 0}$ D、 ${x | - \frac{1}{e} < x < 0$ 或 $\frac{1}{e} < x < π$ 或 $（ 2 n - 1 ） π < x < 2 n π ， n \in Z ，$ 且 $n \neq 0}$

查看试题解析

二、多选题

9. 下列说法正确的是（）

A、为了更好地开展创文创卫工作，需要对在校中小学生参加社会实践活动的意向进行调查，拟采用分层抽样的方法从该地区ABCD四个学校中抽取一个容量为400的样本进行调查，已知ABCD四校人数之比为7∶4∶3∶6，则应从B校中抽取的样本数量为80 B、6件产品中有4件正品，2件次品，从中任取2件，则至少取到1件次品的概率为0.6 C、已知变量x、y线性相关，由样本数据算得线性回归方程是 $\hat{y} = 0.4 x + \hat{a}$ ，且由样本数据算得 $x = 4 ， y = 3.7$ ，则 $\hat{a} = 2.1$ D、箱子中有4个红球、2个白球共6个小球，依次不放回地抽取2个小球，记事件M={第一次取到红球}，N={第二次取到白球}，则M、N为相互独立事件

查看试题解析
10. 如图所示，圆柱OO₁内有一个棱长为2的正方体ABCD-A₁B₁C₁D₁ ，正方体的顶点都在圆柱上下底面的圆周上，E为BD上的动点，则下面选项正确的是（）

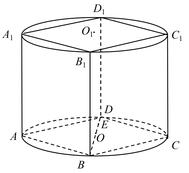A、△ $A_{1} C_{1} E$ 面积的最小值为 $2 \sqrt{2}$ B、圆柱OO₁的侧面积为 $8 \sqrt{2} π$ C、异面直线AD₁与C₁D所成的角为 $6 0^{°}$ D、四面体A₁BC₁D的外接球的表面积为 $12 π$

查看试题解析
11. 已知抛物线C： $x^{2} = 4 y$ 的焦点为 $F$ ，准线为 $l$ ， P是抛物线 $C$ 上第一象限的点， $| P F | = 5$ ，直线PF与抛物线C的另一个交点为Q，则下列选项正确的是（）

A、点P的坐标为（4，4） B、 $| Q F | = \frac{5}{4}$ C、 $S_{△ O P Q} = \frac{10}{3}$ D、过点 $M (x_{0} ， - 1)$ 作抛物线 $C$ 的两条切线 $M A ， M B$ ，其中 $A ， B$ 为切点，则直线 $A B$ 的方程为： $x_{0} x - 2 y + 2 = 0$

查看试题解析
12. 已知点A是圆C： ${(x + 1)}^{2} + y^{2} = 1$ 上的动点，O为坐标原点， $\vec{O A} ⊥ \vec{A B}$ ，且 $| \vec{O A} | = | \vec{A B} |$ ， $O$ ， $A$ ， $B$ 三点顺时针排列，下列选项正确的是（）

A、点 $B$ 的轨迹方程为 ${(x - 1)}^{2} + {(y - 1)}^{2} = 2$ B、 $| C B |$ 的最大距离为 $1 + \sqrt{2}$ C、 $\vec{C A} \cdot \vec{C B}$ 的最大值为 $\sqrt{2} + 1$ D、 $\vec{C A} \cdot \vec{C B}$ 的最大值为 $2$

查看试题解析

三、填空题

13. 已知双曲线C的方程为 $\frac{x^{2}}{4} - y^{2} = 1$ ，则其离心率为．

查看试题解析
14. 函数 $f (x) = \sqrt{3} s i n 2 x + 2 c o s^{2} x$ 在区间 $[- \frac{π}{6} ， \frac{π}{6}]$ 上的最大值为

查看试题解析
15. 已知函数 $f (x) = {\begin{array}{l} | l o g_{2} x | ， 0 < x < 2 \\ - x + 3 ， x \geq 2 \end{array}$ ，若 $x_{1} ， x_{2} ， x_{3}$ 均不相等，且 $f (x_{1}) = f (x_{2}) = f (x_{3})$ ，则 $x_{1} \cdot x_{2} \cdot x_{3}$ 的取值范围是

查看试题解析
16. 如图所示阴影部分是一个美丽的螺旋线型的图案，它的画法是这样的：正三角形 $A B C$ 的边长为4，取正三角形 $A B C$ 各边的四等分点 $D$ ， $E$ ， $F$ ，作第2个正三角形 $D E F$ ，然后再取正三角形 $D E F$ 各边的四等分点 $G$ ， $H$ ， $I$ ，作第3个正三角形 $G H I$ ，依此方法一直继续下去，就可以得到阴影部分的图案 .如图阴影部分，设三角形 $A D F$ 面积为 $S_{1}$ ，后续各阴影三角形面积依次为 $S_{2}$ ， $S_{3}$ ， …， $S_{n}$ ， ….则 $S_{1} =$ ，数列 ${S_{n}}$ 的前 $n$ 项和 $T_{n} =$

查看试题解析

四、解答题

17. 如图所示，遥感卫星发现海面上有三个小岛，小岛 B位于小岛A 北偏东 $7 5^{∘}$ 距离60海里处，小岛B北偏东 $1 5^{∘}$ 距离 $30 \sqrt{3} - 30$ 海里处有一个小岛 C.

(1)、求小岛A到小岛C的距离；

(2)、如果有游客想直接从小岛A出发到小岛 C，求游船航行的方向.

查看试题解析
18. 如图，四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为平行四边形，E为CD的中点， $A E = \frac{1}{2} C D$ .

(1)、证明： $P C ⊥ A D$ ；

(2)、若三角形AED为等边三角形，PA=AD=6，F为PB上一点，且 $P F = \frac{1}{3} P B$ ，求直线EF与平面PAE所成角的正弦值.

查看试题解析
19. 为了增强学生体质，茂名某中学的体育部计划开展乒乓球比赛，为了解学生对乒乓球运动的兴趣，从该校一年级学生中随机抽取了200人进行调查，男女人数相同，其中女生对乒乓球运动有兴趣的占80%，而男生有15人表示对乒乓球运动没有兴趣．
$参考公式： K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)} (n = a + b + c + d)$

(1)、完成2×2列联表，并回答能否有90%的把握认为“对乒乓球运动是否有兴趣与性别有关”？

有兴趣
没兴趣
合计
男
女
合计

(2)、为了提高同学们对比赛的参与度，比赛分两个阶段进行.第一阶段的比赛赛制采取单循环方式，每场比赛采取三局二胜制，然后由积分的多少选出进入第二阶段比赛的同学，每场积分规则如下：比赛中以 $2 ： 0$ 取胜的同学积3分，负的同学积0分；以 $2 ： 1$ 取胜的同学积2分，负的同学积1分.其中，小强同学和小明同学的比赛倍受关注，设每局小强同学取胜的概率为 $p = \frac{2}{3}$ ，记小强同学所得积分为 $X$ ，求 $X$ 的分布列和期望.
附表：
P（K²≥k₀）
0.50
0.40
0.25
0.150
0.100
0.050
k₀
0.455
0.780
1.323
2.072
2.706
3.841

查看试题解析
20. 已知数列 ${a_{n}}$ ， ${b_{n}}$ 满足 $b_{n + 1} = \frac{a_{n} + 4 b_{n}}{5}$ ， $a_{n + 1} = \frac{5 a_{n} + b_{n + 1}}{6}$ ，且 $a_{1} = 2$ ， $b_{1} = 1$

(1)、求 $a_{2}$ ， $b_{2}$ 的值，并证明数列 ${a_{n} - b_{n}}$ 是等比数列；

(2)、求数列 ${a_{n}}$ ， ${b_{n}}$ 的通项公式．

查看试题解析
21. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左焦点为 $F_{1} (- 1 ， 0)$ ，且过点（1， $\frac{3}{2}$ ）.

(1)、求椭圆C的方程；

(2)、过 $F_{1}$ 且互相垂直的两条直线 $l_{1}$ ， $l_{2}$ 分别交椭圆C于A、B两点和 M、N两点，求 $| A B | + | M N |$ 的取值范围.

查看试题解析
22. 已知函数 $f (x) = e^{x} - a x^{3}$ .

(1)、若 $x \in (0 ， + ∞)$ ， $f (x) \geq 0$ 恒成立，求 $a$ 的取值范围；

(2)、证明： $当 a = \frac{2}{3} 时， f (x) > 0$ ；

(3)、证明：当 $n \in N^{*}$ 时， $\frac{1}{e} + \frac{2}{e^{2}} + \frac{3}{e^{3}} + ⋯ + \frac{n}{e^{n}} < 3$ .

查看试题解析

P（K²≥k₀）	0.50	0.40	0.25	0.150	0.100	0.050
k₀	0.455	0.780	1.323	2.072	2.706	3.841

	有兴趣	没兴趣	合计
男
女
合计