备考2022届中考数学全国精选题汇编专题13 数据分析与概率知识及运用
试卷更新日期:2022-02-21 类型:一轮复习
一、单选题
-
1. 某校九年级学生的平均年龄为16岁,年龄的方差为3,若学生人数没有变动,则两年前的同一批学生,对其年龄的说法正确的是( )A、平均年龄为16岁,方差改变 B、平均年龄为14岁,方差不变 C、平均年龄为14岁,方差改变 D、平均年龄为16岁,方差不变2. 实验中学选择10名青少年志愿者参加读书日活动,年龄如表所示:这10名志愿者年龄的众数和中位数分别是( )
年龄
12
13
14
15
人数
2
3
4
1
A、14,13 B、14,14 C、14,13.5 D、13,143. 某鞋厂调查了商场一个月内不同尺码男鞋的销量,在以下统计量中,该鞋厂最关注的是( )A、平均数 B、中位数 C、众数 D、方差4. 在一次献爱心的捐赠活动中,某班40名同学捐款金额统计如下:金额(元)
学生数(人)
在这次活动中,该班同学捐款金额的众数和中位数分别是( )
A、30,35 B、50,40 C、50,50 D、50,455. 小丽准备通过爱心热线捐款,她只记得号码的前5位,后三位由 5,2,0 这三个数字组成,但具体顺序忘记了,她第一次就拨对电话的概率是( )A、 B、 C、 D、6. 我们把三个数的中位数记作Z{a,b,c}.例如Z{1,3,2}=2.函数y=|2x+b|的图象为C1 , 函数y=Z{x+1,﹣x+1,3}的图象为C2 . 图象C1在图象C2的下方点的横坐标x满足﹣3<x<1,则b的取值范围为( )A、0<b<3 B、b>3或b<0 C、0≤b≤3 D、1<b<37. 若样本x1+1,x2+1,…,xn+1的平均数为10,方差为2,则对于样本x1+2,x2+2,…,xn+2,下列结论正确的是( )A、平均数为10,方差为2 B、平均数为11,方差为3 C、平均数为11,方差为2 D、平均数为12,方差为4二、填空题
-
8. 若一组数据1、2、3、4、5的方差是 ,另一组数据101、102、103、104、105的方差是 ,则 (填“>”、“=”或“<”)9. 如图,飞镖游戏板( 方格)中每一块小正方形除标注的数字外都相同,假设飞镖击中每一块小正方形是等可能的(击中小正方形的边界线或没有击中游戏板,则重投1次),任意投掷飞镖1次,击中标有数字“1”的小正方形的概率等于.
1
2
3
2
3
2
2
1
2
3
1
3
3
1
2
1
3
1
2
2
2
3
2
3
1
10. 近年来,我国城乡居民的收入有了大幅提高,为了了解我国城乡居民收入10年来的变化趋势,适合采用的统计图是 .(填“扇形统计图”或“折线统计图”)11. 为了让学生了解环保知识,增强环保意识,某校组织七、八年级各200名学生对相关知识进行学习并组织定时测试.现分别在七、八两个年级中各随机抽取了10名学生,统计这部分学生的测试成绩,相关数据整理如下:七年级:74,86,74,93,81,71,80,87,77,97;
八年级:87,74,94,86,82,76,77,82,78,84.
分别计算两组数据的平均数、中位数、众数、方差,填入下表(部分结果已填入):
年级
平均数
中位数
众数
方差
七年级
82
①
74
66.6
八年级
②
82
③
④
(平均数: ,方差: )
12. 甲、乙两支仪仗队的队员人数相同,平均身高相同,身高的方差分别为S2甲=0.9,S2乙=1.1,则甲、乙两支仪仗队的队员身高更整齐的是(填“甲”或“乙”).13. 甲乙两名同学在10次定点投篮训练中(每次训练投5个),每次训练成绩(投中的个数)如图所示,则甲乙两名同学投篮成绩比较稳定是;(填“甲”或“乙”)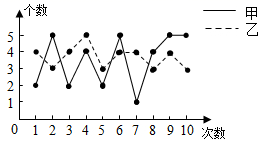 14. 已知一组数据4,x,5,y,7,9的平均数为6,众数为5,则这组数据的中位数为.15. 一组数据为1,3,5,12,a,其中整数a是这组数据的中位数,则该组数据的平均数是.16. 某学校九(1)班40名同学的期中测试成绩分别为 , , ,……, .已知 + + +……+ = 4800,y= + + +……+ ,当y取最小值时, a 的值为.
14. 已知一组数据4,x,5,y,7,9的平均数为6,众数为5,则这组数据的中位数为.15. 一组数据为1,3,5,12,a,其中整数a是这组数据的中位数,则该组数据的平均数是.16. 某学校九(1)班40名同学的期中测试成绩分别为 , , ,……, .已知 + + +……+ = 4800,y= + + +……+ ,当y取最小值时, a 的值为.三、综合题
-
17. 五一期间,甲、乙两人计划在建湖附近的景点游玩,甲从A、B两个景点中任意选择一处游玩,乙从A、B、C三个景点中任意选择一处游玩.(1)、乙恰好游玩A景点的概率为.(2)、求甲、乙恰好游玩同一景点的概率.18. 一只不透明的箱子里有3个球,其中2个白球,1个红球,它们除颜色外均相同.(1)、从箱子中任意摸出一个球是红球的概率是;(2)、从箱子中任意摸出一个球,将它放回箱子,搅匀后再摸出一个球,请用列表的方法,求两次摸出的球一白一红的概率.19. 某校随机抽取了50名九年级学生进行立定跳远水平测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩频数分布表
分组
频数
12
10
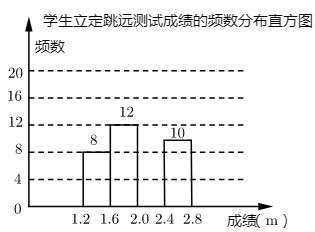
请根据图表中所提供的信息,完成下列问题:
(1)、表中 , , 样本成绩的中位数落在范围内;(2)、请把频数分布直方图补充完整;(3)、该校九年级组共有1200名学生,请估计该校九年级学生立定跳远成绩在 范围内的有多少人?20. 九年级某班要召开一次“走进祖国英雄,讲好中国故事”主题班会活动,张老师制作了编号为A、B、C、D的4张卡片(如图,除了编号和内容外,其余完全相同),将它们背面朝上洗匀后放在桌面上.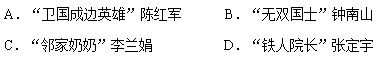 (1)、小东随机抽取1张卡片,则抽到卡片编号为B的概率为;(2)、小东从4张卡片中随机抽取一张(不放回),小海再从余下的3张卡片中随机抽取1张,然后根据抽取的卡片讲述相应英雄故事,求小东、小海两人中恰好有一人讲述“卫国边英雄”陈红军故事的概率(请用“画树状图”或“列表”等方法写出过程)21. 在抛物线 中,规定:(1)符号 称为该抛物线的“抛物线系数”;(2)如果一条抛物线与 轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(1)、小东随机抽取1张卡片,则抽到卡片编号为B的概率为;(2)、小东从4张卡片中随机抽取一张(不放回),小海再从余下的3张卡片中随机抽取1张,然后根据抽取的卡片讲述相应英雄故事,求小东、小海两人中恰好有一人讲述“卫国边英雄”陈红军故事的概率(请用“画树状图”或“列表”等方法写出过程)21. 在抛物线 中,规定:(1)符号 称为该抛物线的“抛物线系数”;(2)如果一条抛物线与 轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.完成下列问题:
(1)、若一条抛物线的系数是 ,则此抛物线的函数表达式为 , 当 满足时,此抛物线没有“抛物线三角形”;(2)、若抛物线 的“抛物线三角形”是等腰直角三角形,求出抛物线系数为 的“抛物线三角形”的面积;(3)、在抛物线 中,系数 均为绝对值不大于 的整数,求该抛物线的“抛物线三角形”是等腰直角三角形的概率.22. 某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学就餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.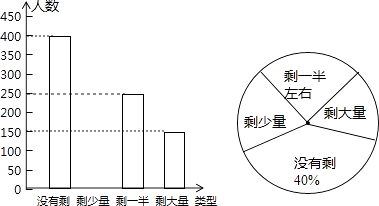 (1)、这次被调查的同学共有名;(2)、补全条形统计图;(3)、计算在扇形统计图中剩大量饭菜所对应扇形圆心角的度数;
(1)、这次被调查的同学共有名;(2)、补全条形统计图;(3)、计算在扇形统计图中剩大量饭菜所对应扇形圆心角的度数;
(4)、校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校20000名学生一餐浪费的食物可供多少人食用一餐?23. 为了解某校九年级320名男生体育中考的成绩情况,从中随机抽取部分男生进行测试,并把测试成绩分为A、B、C、D四个等次,绘制成如图所示的不完整的统计图,请你依图回答下列问题. (1)、a= , b= , c=;(2)、若成绩达到C、D即为优秀,估计该校男生体育成绩优秀人数.24. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好.
(1)、a= , b= , c=;(2)、若成绩达到C、D即为优秀,估计该校男生体育成绩优秀人数.24. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好. (1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)25. 为迎接党的百年华诞,某校举办党史知识竞赛,并从中抽取了部分学生的成绩进行统计(满分 分,成绩不低于50分),绘制了如下不完整的统计图表.
(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)25. 为迎接党的百年华诞,某校举办党史知识竞赛,并从中抽取了部分学生的成绩进行统计(满分 分,成绩不低于50分),绘制了如下不完整的统计图表.分数段频数分布表
分数段/分
人数
频率
2
0.04
8
0.16
0.24
24
4
0.08

根据以上信息,完成下列问题:
(1)、本次调查抽取了多少名学生?(2)、求出表中 的值;(3)、将频数分布直方图不全完整;(4)、若甲同学的竞赛成绩是所统计成绩的中位数,则他的成绩落在哪个分数段内?26. 抽屉 中有白袜、黑袜、红袜、蓝袜各 只,抽屉 中有白袜、黑袜各 只,六只袜子除颜色外无其它差别,相同颜色的两只可组成一双袜子.(1)、小明分别从两个抽屉中随机取一只,求组成一双袜子的概率.(2)、小明从抽屉 中取出两只放入抽屉 中,可组成两双袜子的概率是.27. 某校组织学生参加“防疫卫生知识竞赛”(满分为150分),为了了解某班学生在这次竞赛中的表现,现随机抽取该班10名同学的竞赛成绩制表如下:成绩
148
121
90
88
86
85
81
学生数
1
2
1
1
1
3
1
请根据表中信息,解答下列问题:
(1)、这10名学生竞赛成绩的平均数是分,中位数是分;(2)、甲、乙两人分别用样本的平均数和中位数来推断该班全体学生本次竞赛的情况,请你写出甲、乙两人的推断结论;(3)、指出(2)中谁的推断能较为合理地能反映出该班全体学生本次竞赛的真实水平,并说出另一个人的推断不合理的原因.28. 小李家准备购买一台台式电脑,小李将收集到的该地区 , , 三种品牌电脑销售情况的有关数据统计如下:
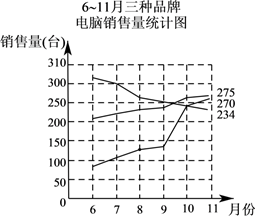
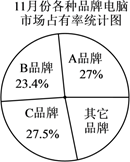
根据上述三个统计图,请解答:
(1)、直接写出6至11月三种品牌电脑销售总量最多的电脑品牌,以及11月份A品牌电脑的销售量;(2)、11月份,其它品牌的电脑销售总量是多少台?(3)、你建议小李购买哪种品牌的电脑?请写出你的理由(写出一条理由即可).29. 为纪念并缅怀当今神农袁隆平为解决人类温饱问题所建立的丰功伟绩,扎实推进“光盘行动”,某校八年级举办“缅怀伟人,拒绝浪费,从我做起”的学生演讲比赛,八(1)班准备从小怡、小宏、小童、小灿4名同学之中选择两名参加比赛,选择方案如下:制作4张完全相同的卡片,正面分别写上这4名同学的姓名,将卡片反面朝上洗匀,张老师从4张卡片中随机抽取1张卡片不放回,再抽取一张,卡片正面是谁的名字,谁就代表班级参加比赛.(注:可以用 、 、 、 分别表示小怡、小宏、小童、小灿的名字)(1)、用树状图或列表法列出所有等可能结果;(2)、求小怡和小宏同时被选中的概率.30. 由中宣部建设的“学习强国”学习平台正式上线,这是推动习近平新时代中国特色社会主义思想,推进马克思主义学习型政党和学习型社会建设的创新举措.某基层党组织对党员的某天学习成绩进行了整理,分成5个小组(x表示成绩,单位:分,且20≤x<70),根据学习积分绘制出部分频数分布表,其中第2、第5两组测试成绩人数之比为4:1,请结合下表中相关数据回答问题:学习积分频数分布表
组别
成绩x分
频数
频率
第1组
20≤x<30
5
第2组
30≤x<40
第3组
40≤x<50
15
0.30
第4组
50≤x<60
10
第5组
60≤x<70
a
b
(1)、填空:a= , b=;(2)、已知该基层党组织中甲、乙两位党员的学习积分分别为63分、67分,现在从这组中随机选取2人介绍经验,请用列表、画树状图等方法,求出甲、乙两人同时被选中的概率.31. 某校为了解九年级同学的体育考试准备情况,随机抽查该年级若干名学生进行体育模拟测试,根据测试成绩(单位:分)绘制成两幅不完整的统计图.请根据图中信息回答下面的问题: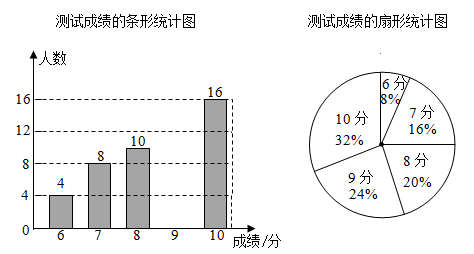 (1)、请补全条形统计图:(2)、所调查学生测试成绩的平均数为 , 中位数为 , 众数为;(3)、若该校九年级学生共有1500人,请估计该校九年级学生在体育模拟测试中不低于8分的学生约有多少人?32. 已知不等式组(1)、求不等式组的解集,并写出它的所有整数解;(2)、在不等式组的所有整数解中任取两个不同的整数相乘,请用画树状图或列表的方法求积为非负数的概率.33. 为了解某校学生的课余兴趣爱好情况,某调查小组设计了“阅读”、“打球”、“书法”和“舞蹈”四个选项,用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况(每个学生必须选一项且只能选一项),并根据调查结果绘制了如图统计图:
(1)、请补全条形统计图:(2)、所调查学生测试成绩的平均数为 , 中位数为 , 众数为;(3)、若该校九年级学生共有1500人,请估计该校九年级学生在体育模拟测试中不低于8分的学生约有多少人?32. 已知不等式组(1)、求不等式组的解集,并写出它的所有整数解;(2)、在不等式组的所有整数解中任取两个不同的整数相乘,请用画树状图或列表的方法求积为非负数的概率.33. 为了解某校学生的课余兴趣爱好情况,某调查小组设计了“阅读”、“打球”、“书法”和“舞蹈”四个选项,用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况(每个学生必须选一项且只能选一项),并根据调查结果绘制了如图统计图: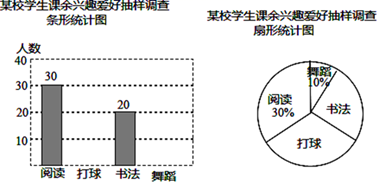
根据统计图所提供的信息,解答下列问题:
(1)、本次抽样调查中的学生人数是;(2)、补全条形统计图;(3)、若该校共有1000名学生,请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数.34. 为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成两幅不完整的统计图,请结合图中所给信息解答下列问题: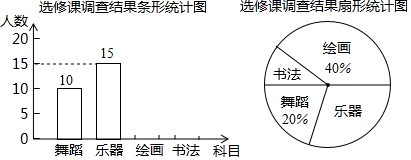 (1)、参与随机抽样问卷调查的有 ▲ 名学生,并补全条形统计图;(2)、扇形统计图中,“乐器”所对应的圆心角度数是°;(3)、若该校有600名学生,估计选修书法的学生大约有多少名?35. 如图是我们熟悉的电路图,其中L1、L2、L3代表灯泡,K1、K2、K3、K4代表开关,R代表电阻.
(1)、参与随机抽样问卷调查的有 ▲ 名学生,并补全条形统计图;(2)、扇形统计图中,“乐器”所对应的圆心角度数是°;(3)、若该校有600名学生,估计选修书法的学生大约有多少名?35. 如图是我们熟悉的电路图,其中L1、L2、L3代表灯泡,K1、K2、K3、K4代表开关,R代表电阻.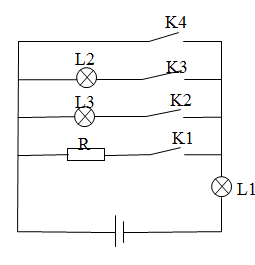 (1)、合上一个开关,有两盏灯亮的概率是;(2)、合上两个开关,有两盏灯亮的概率是多少?请结合树状图或表格解决问题.36. 某区初中有 名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了 名学生的得分(得分取正整数,满分 分)进行统计:
(1)、合上一个开关,有两盏灯亮的概率是;(2)、合上两个开关,有两盏灯亮的概率是多少?请结合树状图或表格解决问题.36. 某区初中有 名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了 名学生的得分(得分取正整数,满分 分)进行统计:
频率分布表分 组 频数 频率 49.5~59.5 25 59.5~69.5 40 0.08 69.5~79.5 0.20 79.5~89.5 155 89.5~100.5 180 0.36 合 计 500 1
请你根据不完整的频率分布表.解答下列问题:
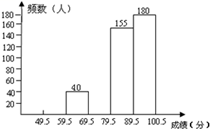
(1)、补全频率分布表;(2)、补全频数分布直方图;(3)、若将得分转化为等级,规定得分低于 分评为“ ”, 分评为“ ”, 分评为“ ”, 分评为“ ”,估计这次 名学生中约有多少人评为“ ”?37. 如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2)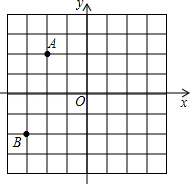 (1)、若点C与点A关于原点O对称,则点C的坐标为;(2)、将点A向右平移5个单位得到点D,则点D的坐标为;(3)、由点A,B,C,D组成的四边形ABCD内(不包括边界)任取一个横、纵坐标均为整数的点,求所取的点横、纵坐标之和恰好为零的概率.38. “节约用水、人人有责”,某班学生利用课余时间对金辉小区300户居民的用水情况进行了统计,发现5月份各户居民的用水量比4月份有所下降,并且将5月份各户居民的节水量统计整理成如图所示的统计图表
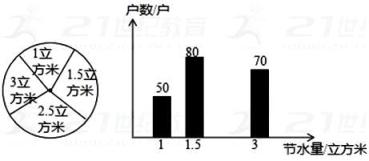
(1)、若点C与点A关于原点O对称,则点C的坐标为;(2)、将点A向右平移5个单位得到点D,则点D的坐标为;(3)、由点A,B,C,D组成的四边形ABCD内(不包括边界)任取一个横、纵坐标均为整数的点,求所取的点横、纵坐标之和恰好为零的概率.38. “节约用水、人人有责”,某班学生利用课余时间对金辉小区300户居民的用水情况进行了统计,发现5月份各户居民的用水量比4月份有所下降,并且将5月份各户居民的节水量统计整理成如图所示的统计图表节水量/立方米
1
1.5
2.5
3
户数/户
50
80
a
70
 (1)、写出统计表中a的值和扇形统计图中2.5立方米对应扇形的圆心角度数.(2)、根据题意,将5月份各居民的节水量的条形统计图补充完整.(3)、求该小区300户居民5月份平均每户节约用水量,若用每立方米水需4元水费,请你估算每户居民1年可节约多少元钱的水费?39. 为了解某县2014年初中毕业生的实验成绩等级的分布情况,随机抽取了该县若干名学生的实验成绩进行统计分析,并根据抽取的成绩绘制了如图所示的统计图表:
(1)、写出统计表中a的值和扇形统计图中2.5立方米对应扇形的圆心角度数.(2)、根据题意,将5月份各居民的节水量的条形统计图补充完整.(3)、求该小区300户居民5月份平均每户节约用水量,若用每立方米水需4元水费,请你估算每户居民1年可节约多少元钱的水费?39. 为了解某县2014年初中毕业生的实验成绩等级的分布情况,随机抽取了该县若干名学生的实验成绩进行统计分析,并根据抽取的成绩绘制了如图所示的统计图表:成绩等级
A
B
C
D
人数
60
x
y
10
百分比
30%
50%
15%
m
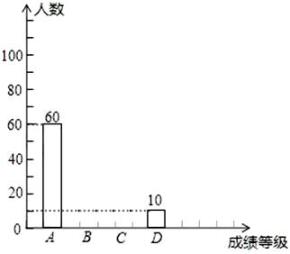
请根据以上统计图表提供的信息,解答下列问题:
(1)、本次抽查的学生有名;(2)、表中x,y和m所表示的数分别为:x= , y= , m=;(3)、请补全条形统计图;(4)、若将抽取的若干名学生的实验成绩绘制成扇形统计图,则实验成绩为D类的扇形所对应的圆心角的度数是多少.40. 在一个不透明的袋子里装有4个标有-1,-2,3,4的小球,它们的形状、大小完全相同.李强从布袋里随机取出一个小球,记下数字为x,王芳在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点M的坐标(x,y).求点M(x,y)在函数y=-x+2的图象上的概率.(用画树状图或列表的方法)