备考2022届中考数学全国精选题汇编专题12 圆的性质及应用
试卷更新日期:2022-02-21 类型:一轮复习
一、填空题
-
1. 小明很喜欢钻研问题,一次数学杨老师拿来一个残缺的圆形瓦片(如图所示)让小明求瓦片所在园的半径,小明连接瓦片弧线两端AB,量的弧AB的中心C到AB的距离CD=1.6cm,AB=6.4cm,很快求得圆形瓦片所在园的半径为 cm.
 2. 如图,在矩形ABCD中,AB=2cm,AD= cm以点B为圆心,AB长为半径画弧,交CD于点E,则图中阴影部分的面积为 cm2.
2. 如图,在矩形ABCD中,AB=2cm,AD= cm以点B为圆心,AB长为半径画弧,交CD于点E,则图中阴影部分的面积为 cm2.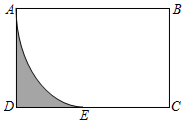 3. 如图,方老师用一张半径为18cm的扇形纸板,做了一个圆锥形帽子(接缝忽略不计).如果圆锥形帽子的半径是10cm,那么这张扇形纸板的面积是 cm2(结果用含π的式子表示).
3. 如图,方老师用一张半径为18cm的扇形纸板,做了一个圆锥形帽子(接缝忽略不计).如果圆锥形帽子的半径是10cm,那么这张扇形纸板的面积是 cm2(结果用含π的式子表示).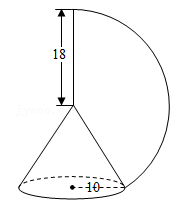 4. 如图, 为正六边形, 为正方形,连接CG,则∠BCG+∠BGC=.
4. 如图, 为正六边形, 为正方形,连接CG,则∠BCG+∠BGC=. 5. 如图,传送带的一个转动轮的半径为 ,转动轮转 ,传送带上的物品 被传送 ,则 .
5. 如图,传送带的一个转动轮的半径为 ,转动轮转 ,传送带上的物品 被传送 ,则 .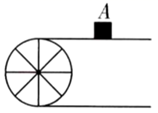 6. 点 是 的外心,若 ,则 为.7. 如图, 是 的直径, 是 的弦, 于D,连接 ,过点D作 交 于F,过点B的切线交 的延长线于E.若 , ,则 .
6. 点 是 的外心,若 ,则 为.7. 如图, 是 的直径, 是 的弦, 于D,连接 ,过点D作 交 于F,过点B的切线交 的延长线于E.若 , ,则 . 8. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积之和是cm2
8. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积之和是cm2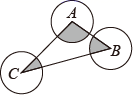 9. 边长为 的正六边形,它的外接圆与内切圆半径的比值是 .10. 如图,在平面直角坐标系 中,点A在 轴负半轴上,点B在 轴正半轴上,⊙D经过A , B , O , C四点,∠ACO=120°,AB=4,则圆心点D的坐标是
9. 边长为 的正六边形,它的外接圆与内切圆半径的比值是 .10. 如图,在平面直角坐标系 中,点A在 轴负半轴上,点B在 轴正半轴上,⊙D经过A , B , O , C四点,∠ACO=120°,AB=4,则圆心点D的坐标是 11. 如图,正六边形ABCDEF的周长是24cm,连接这个六边形的各边中点G,H,K,L,M,N,则六边形GHKLMN的周长是 cm.
11. 如图,正六边形ABCDEF的周长是24cm,连接这个六边形的各边中点G,H,K,L,M,N,则六边形GHKLMN的周长是 cm.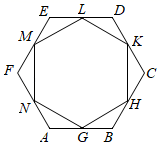 12. 如图,在平面直角坐标系中,以 为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,则点B的坐标是.
12. 如图,在平面直角坐标系中,以 为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,则点B的坐标是. 13. 如图,在圆内接五边形ABCDE中,∠EAB∠+∠C+∠CDE+∠E=430°,则∠CDA=度.
13. 如图,在圆内接五边形ABCDE中,∠EAB∠+∠C+∠CDE+∠E=430°,则∠CDA=度. 14. 如图, 内接于 , ,点 是 的中点,连接 , , ,则 .
14. 如图, 内接于 , ,点 是 的中点,连接 , , ,则 .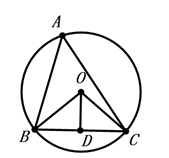
二、作图题
-
15. 尺规作图(只保留作图痕迹,不要求写出作法),如图,已知 ABC,且AB>AC.
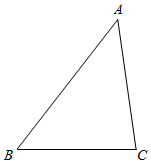
( 1 )在AB边上求作点D,使DB=DC;
( 2 )在AC边上求作点E,使 ADE∽ ACB.
三、解答题
-
16. 已知 内接于 ,点D是 上一点.
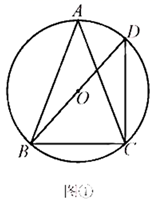

(Ⅰ)如图①,若 为 的直径,连接 ,求 和 的大小;
(Ⅱ)如图②,若 // ,连接 ,过点D作 的切线,与 的延长线交于点E,求 的大小.
四、综合题
-
17. 如图, 是 的外接圆,点E是 的内心,AE的延长线交BC于点F,交 于点D,连接BD,BE.
 (1)、求证: ;(2)、若 , ,求DB的长.18. 如图,在△ABC中,AB=AC,DE⊥AC交BA的延长线于点E,交AC于点F.
(1)、求证: ;(2)、若 , ,求DB的长.18. 如图,在△ABC中,AB=AC,DE⊥AC交BA的延长线于点E,交AC于点F.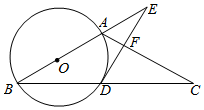 (1)、求证:DE是⊙O的切线;
(1)、求证:DE是⊙O的切线;
(2)、若AC=6,tanE= ,求AF的长.
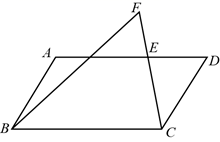
19. 如图,在等腰锐角三角形ABC中,AB=AC,过点B作BD⊥AC于D,延长BD交△ABC的外接圆于点E,过点A作AF⊥CE于F,AE,BC的延长线交于点G.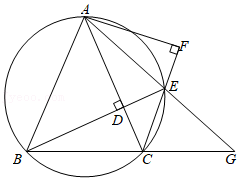 (1)、判断EA是否平分∠DEF,并说明理由;(2)、求证:①BD=CF;
(1)、判断EA是否平分∠DEF,并说明理由;(2)、求证:①BD=CF;②BD2=DE2+AE•EG.
20. 如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,点D是 的中点,DE∥BC交AC的延长线于点E.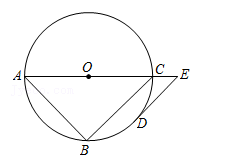 (1)、求证:直线DE与⊙O相切;(2)、若⊙O的直径是10,∠A=45°,求CE的长.21. 如图,直线 经过 上的点 ,直线 与 交于点 和点 , 与 交于点 ,与 交于点 , , .
(1)、求证:直线DE与⊙O相切;(2)、若⊙O的直径是10,∠A=45°,求CE的长.21. 如图,直线 经过 上的点 ,直线 与 交于点 和点 , 与 交于点 ,与 交于点 , , . (1)、求证: 是 的切线;(2)、若 , ,求图中阴影部分面积.22. 如图, 、 是 的切线, 、 是切点, 是 的直径,连接 ,交 于点 ,交 于点 .
(1)、求证: 是 的切线;(2)、若 , ,求图中阴影部分面积.22. 如图, 、 是 的切线, 、 是切点, 是 的直径,连接 ,交 于点 ,交 于点 .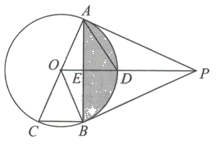 (1)、求证: ;(2)、若 恰好是 的中点,且四边形 的面积是 ,求阴影部分的面积;(3)、若 ,且 ,求切线 的长.23. 如图,在 中, 为 的直径, 为 的弦,点 是 的中点,过点 作 的垂线,交 于点 ,交 于点 ,分别连接 .
(1)、求证: ;(2)、若 恰好是 的中点,且四边形 的面积是 ,求阴影部分的面积;(3)、若 ,且 ,求切线 的长.23. 如图,在 中, 为 的直径, 为 的弦,点 是 的中点,过点 作 的垂线,交 于点 ,交 于点 ,分别连接 .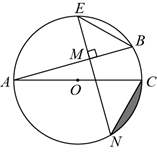 (1)、 与 的数量关系是;(2)、求证: ;(3)、若 ,求阴影部分图形的面积.24. 如图,在 中, , ,以点 为圆心, 为半径的圆交 的延长线于点 ,过点 作 的平行线,交 于点 ,连接 .
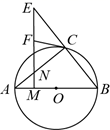
(1)、 与 的数量关系是;(2)、求证: ;(3)、若 ,求阴影部分图形的面积.24. 如图,在 中, , ,以点 为圆心, 为半径的圆交 的延长线于点 ,过点 作 的平行线,交 于点 ,连接 . (1)、求证: 为 的切线;(2)、若 ,求弧 的长.25. 如图,点A在以 为直径的⊙ 上, 的角平分线与 相交于点E,与⊙ 相交于点D,延长 至M,连结 ,使得 ,过点A作 的平行线与 的延长线交于点N.
(1)、求证: 为 的切线;(2)、若 ,求弧 的长.25. 如图,点A在以 为直径的⊙ 上, 的角平分线与 相交于点E,与⊙ 相交于点D,延长 至M,连结 ,使得 ,过点A作 的平行线与 的延长线交于点N. (1)、求证: 与⊙ 相切;(2)、试给出 之间的数量关系,并予以证明.26. 如图, 为 直径,D为 上一点, 于点C,交 于点E, 与 的延长线交于点F, 平分 .
(1)、求证: 与⊙ 相切;(2)、试给出 之间的数量关系,并予以证明.26. 如图, 为 直径,D为 上一点, 于点C,交 于点E, 与 的延长线交于点F, 平分 .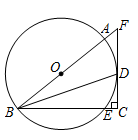 (1)、求证: 是 的切线;(2)、若 ,求 和 的长.27. 如图,AB是 直径,弦 ,垂足为点E . 弦BF交CD于点G , 点P在CD延长线上,且 .
(1)、求证: 是 的切线;(2)、若 ,求 和 的长.27. 如图,AB是 直径,弦 ,垂足为点E . 弦BF交CD于点G , 点P在CD延长线上,且 .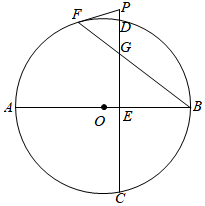 (1)、求证:PF为 切线;(2)、若 , , ,求PF的长.28. 如图,已知 中, .
(1)、求证:PF为 切线;(2)、若 , , ,求PF的长.28. 如图,已知 中, . (1)、请按如下要求完成尺规作图.(不写作法,保留作图痕迹)
(1)、请按如下要求完成尺规作图.(不写作法,保留作图痕迹)① 的角平分线 ,交 于点D;
②作线段 的垂直平分线 与 相交于点O;
③以点O为圆心,以 长为半径画圆,交边 于点M.
(2)、在(1)的条件下求证: 是 的切线;(3)、若 , ,求 的半径.29. 如图,已知 内接干 , 是 的直径, 的平分线交 于点 ,交 于点 ,连接 ,作 ,交 的延长线于点 .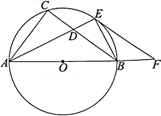 (1)、求证: 是 的切线;(2)、若 , ,求 的半径和 的长.30. 如图,在 中, , 是 上的一点,以 为直径的 与 相切于点 ,连接 , .
(1)、求证: 是 的切线;(2)、若 , ,求 的半径和 的长.30. 如图,在 中, , 是 上的一点,以 为直径的 与 相切于点 ,连接 , .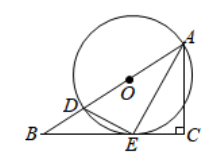 (1)、求证: 平分 ;(2)、若 ,求 的值.31. 如图,PM、PN是⊙O的切线,切点分别是A、B,过点O的直线CE∥PN,交⊙O于点C、D,交PM于点E,AD的延长线交PN于点F,若BC∥PM.
(1)、求证: 平分 ;(2)、若 ,求 的值.31. 如图,PM、PN是⊙O的切线,切点分别是A、B,过点O的直线CE∥PN,交⊙O于点C、D,交PM于点E,AD的延长线交PN于点F,若BC∥PM.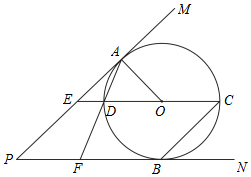 (1)、求证:∠P=45°;(2)、若CD=6,求PF的长.32. 如图,在Rt△ACD中,∠ACD=90°,点O在CD上,作⊙O,使⊙O与AD相切于点B,⊙O与CD交于点E,过点D作DF∥AC,交AO的延长线于点F,且∠OAB=∠F.
(1)、求证:∠P=45°;(2)、若CD=6,求PF的长.32. 如图,在Rt△ACD中,∠ACD=90°,点O在CD上,作⊙O,使⊙O与AD相切于点B,⊙O与CD交于点E,过点D作DF∥AC,交AO的延长线于点F,且∠OAB=∠F.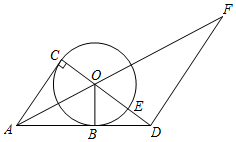 (1)、求证:AC是⊙O的切线;(2)、若OC=3,DE=2,求tan∠F的值.33. 如图,已知:AB为⊙O的直径,⊙O交△ABC于点D、E,点F为AC的延长线上一点,且∠CBF ∠BOE.
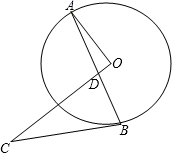
(1)、求证:AC是⊙O的切线;(2)、若OC=3,DE=2,求tan∠F的值.33. 如图,已知:AB为⊙O的直径,⊙O交△ABC于点D、E,点F为AC的延长线上一点,且∠CBF ∠BOE.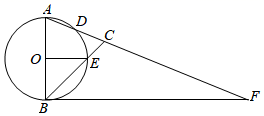 (1)、求证:BF是⊙O的切线;(2)、若AB=4 ,∠CBF=45°,BE=2EC,求AD和CF的长.34. 如图,AB是⊙O的直径,OC是半径,延长OC至点D.连接AD,AC,BC.使∠CAD=∠B.
(1)、求证:BF是⊙O的切线;(2)、若AB=4 ,∠CBF=45°,BE=2EC,求AD和CF的长.34. 如图,AB是⊙O的直径,OC是半径,延长OC至点D.连接AD,AC,BC.使∠CAD=∠B.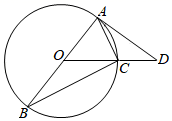 (1)、求证:AD是⊙O的切线;(2)、若AD=4,tan∠CAD= ,求BC的长.35.(1)、某运输队第一次运输360吨化肥,装载了6节火车车厢和15辆汽车;第二次装载了8节火车车厢和10辆汽车,比第一次多运输了化肥80吨.每节火车车厢与每辆汽车平均各装多少吨化肥?(2)、如图,AB是 的直径,点C在 上,AD垂直于过点C的切线,垂足为D,CE垂直AB,垂足为E.求证 .
(1)、求证:AD是⊙O的切线;(2)、若AD=4,tan∠CAD= ,求BC的长.35.(1)、某运输队第一次运输360吨化肥,装载了6节火车车厢和15辆汽车;第二次装载了8节火车车厢和10辆汽车,比第一次多运输了化肥80吨.每节火车车厢与每辆汽车平均各装多少吨化肥?(2)、如图,AB是 的直径,点C在 上,AD垂直于过点C的切线,垂足为D,CE垂直AB,垂足为E.求证 .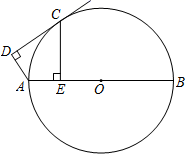 36. 如图
36. 如图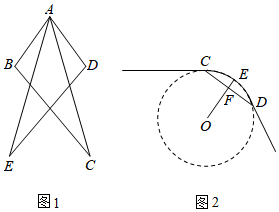 (1)、风筝起源于中国,至今已有2300多年的历史,如图1,在小明设计的“风筝”图案中,已知 , , .求证: ;(2)、如图2,一条公路的转弯处是一段圆弧,点 是弧 的圆心, 为弧 上一点, ,垂足为 .已知 , ,求这段弯路的半径.37. 如图1, 中, ,半径为r的 经过点A且与 相切,切点M在线段 上(包含点M与点B、C重合的情况).
(1)、风筝起源于中国,至今已有2300多年的历史,如图1,在小明设计的“风筝”图案中,已知 , , .求证: ;(2)、如图2,一条公路的转弯处是一段圆弧,点 是弧 的圆心, 为弧 上一点, ,垂足为 .已知 , ,求这段弯路的半径.37. 如图1, 中, ,半径为r的 经过点A且与 相切,切点M在线段 上(包含点M与点B、C重合的情况).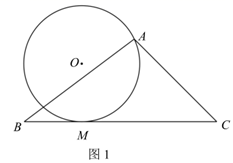
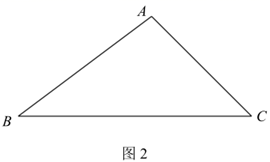 (1)、半径r的最小值等于:(2)、设 ,求半径r关于x的函数表达式;(3)、当 时,请在图2中作出点M及满足条件的 .
(1)、半径r的最小值等于:(2)、设 ,求半径r关于x的函数表达式;(3)、当 时,请在图2中作出点M及满足条件的 .(要求:尺规作图,不写作法,保留作图痕迹,并用2B铅笔或黑色水笔加黑加粗)
-
-