备考2022届中考数学全国精选题汇编专题11 三角形和四边形知识运用
试卷更新日期:2022-02-21 类型:一轮复习
一、单选题
-
1. 如图,在4×4的正方形网格中,记∠ABF= ,∠FCH= ,∠DGE= ,则( )
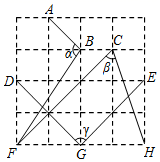 A、 < < B、 ≤ < C、 < < D、 < <2. 函数y= x﹣3的图象与x轴、y轴分别交于A、B两点,点C在x轴上.若△ABC为等腰三角形,则满足条件的点C共有( )A、4个 B、3个 C、2个 D、1个3. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,将△ABC绕点A沿顺时针方向旋转后得到△ADE,直线BD、CE相交于点O,连接AO.则下列结论中:①△ABD∽△ACE;②∠COD=135°;③AO⊥BD;④△AOC面积的最大值为8,其中正确的有( )
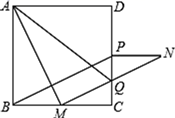
A、 < < B、 ≤ < C、 < < D、 < <2. 函数y= x﹣3的图象与x轴、y轴分别交于A、B两点,点C在x轴上.若△ABC为等腰三角形,则满足条件的点C共有( )A、4个 B、3个 C、2个 D、1个3. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,将△ABC绕点A沿顺时针方向旋转后得到△ADE,直线BD、CE相交于点O,连接AO.则下列结论中:①△ABD∽△ACE;②∠COD=135°;③AO⊥BD;④△AOC面积的最大值为8,其中正确的有( )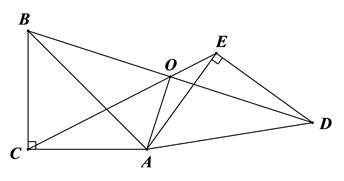 A、1个 B、2个 C、3个 D、4个4. 如图,在Rt△ABC中,∠ACB=90°,AC=3,D是边AB上一点,连结CD,将△ACD沿CD翻折得到△ECD,连结BE.若四边形BCDE是平行四边形,则BC的长为( )
A、1个 B、2个 C、3个 D、4个4. 如图,在Rt△ABC中,∠ACB=90°,AC=3,D是边AB上一点,连结CD,将△ACD沿CD翻折得到△ECD,连结BE.若四边形BCDE是平行四边形,则BC的长为( )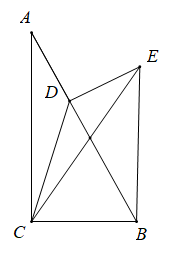 A、 B、3 C、2 D、35. 如图, 中, , ,垂足为D,P为直线BC上方的一个动点,过点Р作 ,垂足为E,若 ,则 的最小值为( )
A、 B、3 C、2 D、35. 如图, 中, , ,垂足为D,P为直线BC上方的一个动点,过点Р作 ,垂足为E,若 ,则 的最小值为( )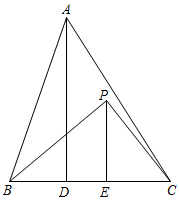 A、4 B、 C、3 D、6. 如图,在 中,作以 为内角,四个顶点都在 边上的菱形时,如下的作图步骤是打乱的.①分别以点A、G圆心,大于 长为半径在AG两侧作弧,两弧相交于点M、N;②作直线MN分别交AB、AC于点P、Q,连接PG、GQ;③分别以点D、E为圆心,大于 的长为半径作弧,两弧相交于 内一点F,连接AF并延长交边BC于点G;④以点A为圆心,适当的长为半径作弧,分别交AB、AC于点D、E.则正确的作图步骤是( )
A、4 B、 C、3 D、6. 如图,在 中,作以 为内角,四个顶点都在 边上的菱形时,如下的作图步骤是打乱的.①分别以点A、G圆心,大于 长为半径在AG两侧作弧,两弧相交于点M、N;②作直线MN分别交AB、AC于点P、Q,连接PG、GQ;③分别以点D、E为圆心,大于 的长为半径作弧,两弧相交于 内一点F,连接AF并延长交边BC于点G;④以点A为圆心,适当的长为半径作弧,分别交AB、AC于点D、E.则正确的作图步骤是( ) A、②④①③ B、④③②① C、②④③① D、④③①②7. 已知点 ,点 为坐标原点,连接 ,将线段 按顺时针方向旋转90°,得 到线段 ,则点 的坐标是( )A、(-1,-2) B、(1,2) C、(2,1) D、(-2,-1)8. 如图,C为线段AB上一点,在线段AB的同侧分别作等边△ACD、△BCE,连接AE、BD相交于F,连接CF.若S△DEF=8 ,则CF的长为( )
A、②④①③ B、④③②① C、②④③① D、④③①②7. 已知点 ,点 为坐标原点,连接 ,将线段 按顺时针方向旋转90°,得 到线段 ,则点 的坐标是( )A、(-1,-2) B、(1,2) C、(2,1) D、(-2,-1)8. 如图,C为线段AB上一点,在线段AB的同侧分别作等边△ACD、△BCE,连接AE、BD相交于F,连接CF.若S△DEF=8 ,则CF的长为( )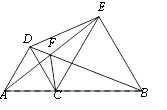 A、4 B、3 C、3 D、4
A、4 B、3 C、3 D、4二、填空题
-
9. 如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为.
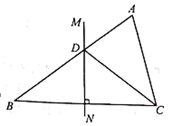 10. 如图,△ABC中,∠BCA=120°,BC=AC,AB=6,以边AB为斜边在△ABC形外作Rt△ADB,使得∠ADB=90°,则四边形ACBD最大面积是.
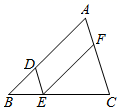
10. 如图,△ABC中,∠BCA=120°,BC=AC,AB=6,以边AB为斜边在△ABC形外作Rt△ADB,使得∠ADB=90°,则四边形ACBD最大面积是.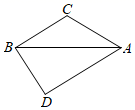 11. 如图,在平行四边形 中, 、 分别是 、 的中点, ,则 的长为.
11. 如图,在平行四边形 中, 、 分别是 、 的中点, ,则 的长为. 12. 如图,在 中, , , 为 边的中点,点E、F分别是线段AC、AD上的动点,且 ,则 的最小值是.
12. 如图,在 中, , , 为 边的中点,点E、F分别是线段AC、AD上的动点,且 ,则 的最小值是.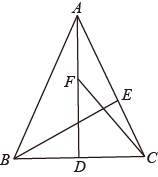 13. 如图,在矩形ABCD中,E是边BC上一点,连接AE,过点B作BF⊥AE于点G,交直线CD于点F.以BE和BF为邻边作平行四边形BEHF,M是BH的中点,连接GM,若AB=3,BC=2,则GM的最小值为.
13. 如图,在矩形ABCD中,E是边BC上一点,连接AE,过点B作BF⊥AE于点G,交直线CD于点F.以BE和BF为邻边作平行四边形BEHF,M是BH的中点,连接GM,若AB=3,BC=2,则GM的最小值为.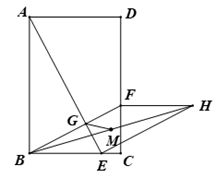 14. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,记 的面积为 ,四边形CDOE的面积为 ,则 .
14. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,记 的面积为 ,四边形CDOE的面积为 ,则 .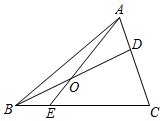 15. 如图,在 中, , , ,菱形 顶点 在边 上, 分别在边 上,则 的取值范围是.
15. 如图,在 中, , , ,菱形 顶点 在边 上, 分别在边 上,则 的取值范围是. 16. 如图,已知DC为∠ACB的平分线,DE∥BC.若AD=8,BD=10,BC=15,求EC的长=.
16. 如图,已知DC为∠ACB的平分线,DE∥BC.若AD=8,BD=10,BC=15,求EC的长=.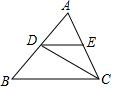 17. 我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积是130,小正方形面积是10,则 的值是.
17. 我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积是130,小正方形面积是10,则 的值是.

 18. 如图,菱形 的两条对角线 相交于点 是 的中点,若 ,则 的长为.
18. 如图,菱形 的两条对角线 相交于点 是 的中点,若 ,则 的长为.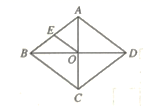 19. 如图,在 中, 是 边上的高, , , ,则 的长为.
19. 如图,在 中, 是 边上的高, , , ,则 的长为.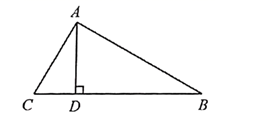 20. 如图,平面直角坐标系中,已知A(2,0),B(4,0),P为y轴正半轴上一个动点,将线段PA绕点P逆时针旋转90°,点A的对应点为Q,则线段BQ的最小值是.
20. 如图,平面直角坐标系中,已知A(2,0),B(4,0),P为y轴正半轴上一个动点,将线段PA绕点P逆时针旋转90°,点A的对应点为Q,则线段BQ的最小值是.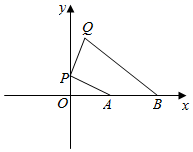 21. 如图,在平面直角坐标系中,A(3,0),B(0,4),M为AB边上的一动点,N(0,1),连接MN,将△ABO绕点O逆时针旋转一周,则MN的取值范围为.
21. 如图,在平面直角坐标系中,A(3,0),B(0,4),M为AB边上的一动点,N(0,1),连接MN,将△ABO绕点O逆时针旋转一周,则MN的取值范围为.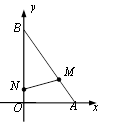 22. 把一张宽为2cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为4cm的等腰直角三角形,则纸片的长AD为 cm.
22. 把一张宽为2cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为4cm的等腰直角三角形,则纸片的长AD为 cm.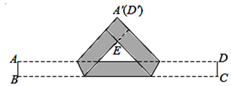 23. 在 中, , , , ,则 的长为.24. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平后再次折叠,使点A落在EF上的点A′处,得到折痕BM,BM与EF相交于点N.若直线BA′交直线CD于点O,BC=5,EN=1,则OD的长为.
23. 在 中, , , , ,则 的长为.24. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平后再次折叠,使点A落在EF上的点A′处,得到折痕BM,BM与EF相交于点N.若直线BA′交直线CD于点O,BC=5,EN=1,则OD的长为.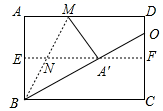 25. 如图,△ABC的顶点在正方形网格的格点上,则sinA的值为.
25. 如图,△ABC的顶点在正方形网格的格点上,则sinA的值为.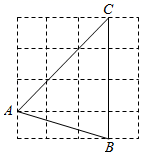 26. 如图, 中, 厘米, 厘米,点 为 的中点,如果点 在线段 上以 厘米/秒的速度由 点向 点运动,同时,点 在线段 上由 点向 点运动.若点 的运动速度为 厘米/秒,则当 与 全等时, 的值为.
26. 如图, 中, 厘米, 厘米,点 为 的中点,如果点 在线段 上以 厘米/秒的速度由 点向 点运动,同时,点 在线段 上由 点向 点运动.若点 的运动速度为 厘米/秒,则当 与 全等时, 的值为.
三、作图题
-
27. 按要求完成下列尺规作图(不写作法,保留作图痕迹).
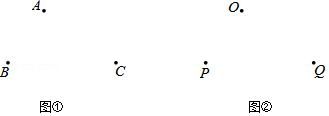 (1)、如图①,点A、B、C是平行四边形ABCD的三个顶点,求作平行四边形ABCD;(2)、如图②,点O、P、Q分别是平行四边形EFGH三边EH、EF、FG的中点,求作平行四边形EFGH.28. 如图,网格小正方形的边长都为 ,在 中,试利用格点分别画出:边AC上的中线BM、边AB上的高CH , 并判断 的形状.
(1)、如图①,点A、B、C是平行四边形ABCD的三个顶点,求作平行四边形ABCD;(2)、如图②,点O、P、Q分别是平行四边形EFGH三边EH、EF、FG的中点,求作平行四边形EFGH.28. 如图,网格小正方形的边长都为 ,在 中,试利用格点分别画出:边AC上的中线BM、边AB上的高CH , 并判断 的形状.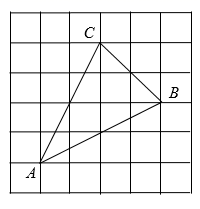
四、解答题
-
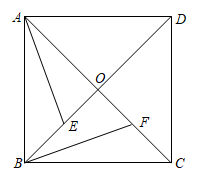
29. 如图,正方形 的对角线 、 相交于点 , 、 分别在 、 上, .写出 与 的关系,并说明理由.
五、综合题
-
30. 如图,将平行四边形ABCD的四个角向内折起,恰好拼成一个无缝隙、无重叠四边形EFGH.
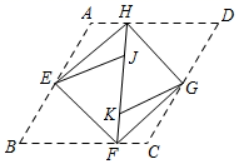 (1)、请直接写出∠HEF的度数;(2)、判断HF与AD的数量关系,并说明理由.31. 如图,△ABC为等边三角形,AB=6,将边AB绕点A顺时针旋转 (0°< <120°)得到线段AD,连接CD,CD与AB交于点G,∠BAD的平分线交CD于点E,F为CD上一点,且DF=2CF.
(1)、请直接写出∠HEF的度数;(2)、判断HF与AD的数量关系,并说明理由.31. 如图,△ABC为等边三角形,AB=6,将边AB绕点A顺时针旋转 (0°< <120°)得到线段AD,连接CD,CD与AB交于点G,∠BAD的平分线交CD于点E,F为CD上一点,且DF=2CF. (1)、当∠EAB=30°时,求∠AEC的度数;(2)、当线段BF的长取最小值时,求线段AG的长;(3)、请直接写出△ADE的周长的最大值.32. 如图,在四边形ABCD中,∠B=90°,AC平分∠DAB,DE⊥AC,垂足为E,且AE=AB.
(1)、当∠EAB=30°时,求∠AEC的度数;(2)、当线段BF的长取最小值时,求线段AG的长;(3)、请直接写出△ADE的周长的最大值.32. 如图,在四边形ABCD中,∠B=90°,AC平分∠DAB,DE⊥AC,垂足为E,且AE=AB.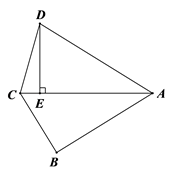 (1)、求证:BC=DE;(2)、若∠DAC=40°,求∠CDE的度数.33. 如图,在矩形ABCD中,P为CD边上一点 ,将 沿AP翻折得到 , 的延长线交边AB于点M,过点B作 交DC于点N.
(1)、求证:BC=DE;(2)、若∠DAC=40°,求∠CDE的度数.33. 如图,在矩形ABCD中,P为CD边上一点 ,将 沿AP翻折得到 , 的延长线交边AB于点M,过点B作 交DC于点N.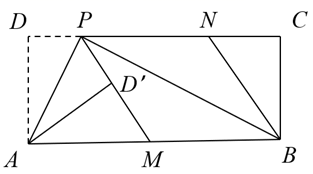 (1)、若 ,
(1)、若 ,①求证 ;
②判断四边形PMBN的形状,并说明理由;
(2)、若 ,求 的值.34. 如图,矩形ABCD对角线AC、BD相交于点O,分别过点D、点A作直线DE∥AC,直线AE∥BD,交于点E.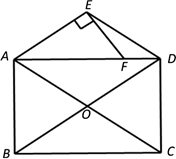 (1)、求证:四边形AODE是菱形;(2)、点E作EF⊥AE交AD于点F,若AB=2,BC=4,求EF.35. 在矩形 中, , ,点 是边 上一动点,连接 ,将 沿 翻折,点 的对应点为点 .
(1)、求证:四边形AODE是菱形;(2)、点E作EF⊥AE交AD于点F,若AB=2,BC=4,求EF.35. 在矩形 中, , ,点 是边 上一动点,连接 ,将 沿 翻折,点 的对应点为点 .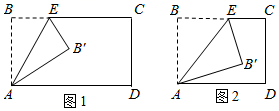 (1)、如图,设 , ,在点 从 点运动到 点的过程中.
(1)、如图,设 , ,在点 从 点运动到 点的过程中.① 最小值是 , 此时x=;
②点 的运动路径长为.
(2)、如图,设 ,当点 的对应点 落在矩形 的边上时,求 的值.36. 如图, 的对角线 、 相交于点 ,过点 作 ,分别交 、 于点 、 ,连接 、 .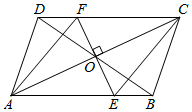 (1)、若 ,求 的长;(2)、判断四边形 的形状,并说明理由.37. 在矩形 中,点 是 边上一点,将 沿 折叠,使点 恰好落在 边上的点 处.
(1)、若 ,求 的长;(2)、判断四边形 的形状,并说明理由.37. 在矩形 中,点 是 边上一点,将 沿 折叠,使点 恰好落在 边上的点 处.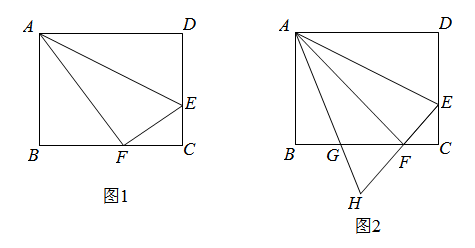 (1)、如图1,若 ,求 的值;(2)、如图2,在线段 上取一点 ,使 平分 ,延长 , 交于点 ,若 ,求 的值.38. 如图,在平行四边形 中, 平分 交 于点F.
(1)、如图1,若 ,求 的值;(2)、如图2,在线段 上取一点 ,使 平分 ,延长 , 交于点 ,若 ,求 的值.38. 如图,在平行四边形 中, 平分 交 于点F.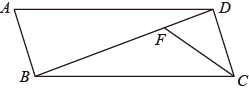 (1)、尺规作图:过点A作 平分 交 于点E;注意:不写作法,保留作图痕迹,并标明字母.(2)、求证: .
(1)、尺规作图:过点A作 平分 交 于点E;注意:不写作法,保留作图痕迹,并标明字母.(2)、求证: .
-