备考2022届中考数学全国精选题汇编专题10 平面几何基本常识快速过关(2)
试卷更新日期:2022-02-21 类型:一轮复习
一、填空题
-
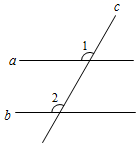
1. 如图,直线a,b被直线c所截,当∠1 ∠2时,a//b.(用“>”,“<”或“=”填空)
 2. 如图,AB∥CD,CB平分∠ECD,若∠B=26°,则∠1的度数是.
2. 如图,AB∥CD,CB平分∠ECD,若∠B=26°,则∠1的度数是.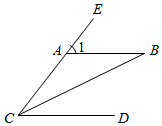 3. 若长度分别为3,4,a的三条线段能组成一个三角形,则整数a的值可以是.(写出一个即可)4. 如图,在⊙O内接四边形 中,若 ,则 .
3. 若长度分别为3,4,a的三条线段能组成一个三角形,则整数a的值可以是.(写出一个即可)4. 如图,在⊙O内接四边形 中,若 ,则 .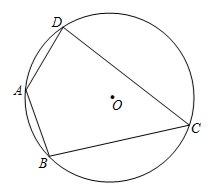 5. 将一副三角板如图摆放,则∥ , 理由是.
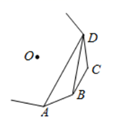
5. 将一副三角板如图摆放,则∥ , 理由是. 6. 如图,已知 , , ,则 .
6. 如图,已知 , , ,则 .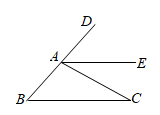 7. 如图,在 的正方形网格图中,已知点A、B、C、D、O均在格点上,其中A、B、D又在 上,点E是线段 与 的交点.则 的正切值为.
7. 如图,在 的正方形网格图中,已知点A、B、C、D、O均在格点上,其中A、B、D又在 上,点E是线段 与 的交点.则 的正切值为.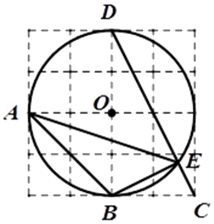 8. 若一条长为32cm的细线能围成一边长等于8cm的等腰三角形,则该等腰三角形的腰长为cm.9. 一个圆锥的侧面展开图是半径为16cm,圆心角为120°的扇形,那么这个圆锥的底面半径为.10. 如图所示的网格是正方形网格,则 (点A,B,C,D,E是网格线交点).
8. 若一条长为32cm的细线能围成一边长等于8cm的等腰三角形,则该等腰三角形的腰长为cm.9. 一个圆锥的侧面展开图是半径为16cm,圆心角为120°的扇形,那么这个圆锥的底面半径为.10. 如图所示的网格是正方形网格,则 (点A,B,C,D,E是网格线交点). 11. 如图,直线 将正九边形 分为两个区域,且分别与 相交于 点、 点.若 ,则 °.
11. 如图,直线 将正九边形 分为两个区域,且分别与 相交于 点、 点.若 ,则 °.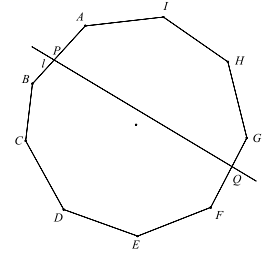 12. 如图,一副三角板按图示放置,已知∠AOC=65°,则∠AOB=°.
12. 如图,一副三角板按图示放置,已知∠AOC=65°,则∠AOB=°.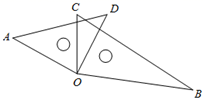 13. 如图,l1∥l2∥l3 , AC交l1、l2、l3分别于A、B、C,且AC=6,BC=4,DF交l1、l2、l3分别于D、E、F,则 =.
13. 如图,l1∥l2∥l3 , AC交l1、l2、l3分别于A、B、C,且AC=6,BC=4,DF交l1、l2、l3分别于D、E、F,则 =. 14. 如图, 是 的直径,弦 ,垂足为点H.若 , ,则 的半径长为.
14. 如图, 是 的直径,弦 ,垂足为点H.若 , ,则 的半径长为.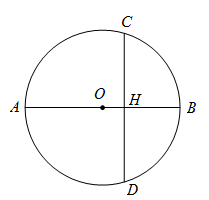 15. 在平面直角坐标系中,已知点 , ,以原点 为位似中心,把 按相似比 缩小,则点 的对应点 的坐标是.16. 如图, 、 分别是 边 、 上的点, , , , ,则 长为 .
15. 在平面直角坐标系中,已知点 , ,以原点 为位似中心,把 按相似比 缩小,则点 的对应点 的坐标是.16. 如图, 、 分别是 边 、 上的点, , , , ,则 长为 .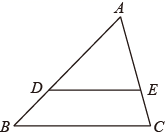 17. 在线段、正三角形、平行四边形、矩形、圆中既是轴对称图形又是中心对称图形的个数为.18. 命题“等腰三角形两底角相等”的逆命题是。19. 如果正多边形的一个外角为45°,那么它的边数是.20. 将一副三角板如图摆放,则 °.
17. 在线段、正三角形、平行四边形、矩形、圆中既是轴对称图形又是中心对称图形的个数为.18. 命题“等腰三角形两底角相等”的逆命题是。19. 如果正多边形的一个外角为45°,那么它的边数是.20. 将一副三角板如图摆放,则 °.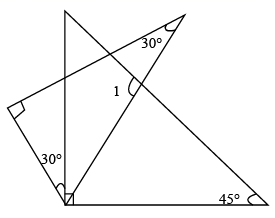 21. 已知四边形 的四个顶点都在 上,则得到结论 .上述推理由因到果的依据是.22. 如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则 的值为.
21. 已知四边形 的四个顶点都在 上,则得到结论 .上述推理由因到果的依据是.22. 如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则 的值为. 23. 图1中的直角三角形有一条直角边长为3,将四个图1中的直角三角形分别拼成如图2,图3所示的正方形,其中阴影部分的面积分别记为 ,则 的值为.
23. 图1中的直角三角形有一条直角边长为3,将四个图1中的直角三角形分别拼成如图2,图3所示的正方形,其中阴影部分的面积分别记为 ,则 的值为. 24. 如图所示的五边形花环是用五个全等的等腰三角形拼成的,则∠BAC的度数为.
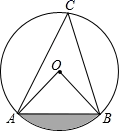
24. 如图所示的五边形花环是用五个全等的等腰三角形拼成的,则∠BAC的度数为. 25. 如图,点A、B、C在 上, ,连接 并延长,交 于点D,连接 、 .若 ,则 的大小为 .
25. 如图,点A、B、C在 上, ,连接 并延长,交 于点D,连接 、 .若 ,则 的大小为 . 26. 如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=.
26. 如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=. 27. 如果一个n边形的外角和是内角和的一半,那么 .28. 小红准备用纸板制作一个底面半径为 ,母线长为 的圆锥形生日礼帽,则这个圆锥形礼帽的侧面积为 .(接缝耗材忽略不计,结果保留 )
27. 如果一个n边形的外角和是内角和的一半,那么 .28. 小红准备用纸板制作一个底面半径为 ,母线长为 的圆锥形生日礼帽,则这个圆锥形礼帽的侧面积为 .(接缝耗材忽略不计,结果保留 )