备考2022届中考数学全国精选题汇编专题7 函数知识的实际应用(1)
试卷更新日期:2022-02-21 类型:一轮复习
一、单选题
-
1. 一位运动员在离篮筐水平距离4m处起跳投篮,球运行路线可看作抛物线,当球离开运动员的水平距离为1m时,它与篮筐同高,球运行中的最大高度为3.5m,最后准确落入篮筐,已知篮筐到地面的距离为3.05m,该运动员投篮出手点距离地面的高度为( )
 A、1.5m B、2m C、2.25m D、2.5m2. 如图,图中的函数图象描述了甲乙两人越野登山比赛.(x表示甲从起点出发所行的时间,表示甲的路程,表示乙的路程).下列4个说法:
A、1.5m B、2m C、2.25m D、2.5m2. 如图,图中的函数图象描述了甲乙两人越野登山比赛.(x表示甲从起点出发所行的时间,表示甲的路程,表示乙的路程).下列4个说法:①越野登山比赛的全程为1000米;
②甲比乙晚出发40分钟;
③甲在途中休息了10分钟;
④乙追上甲时,乙跑了750米.其中正确的说法有( )个
 A、1 B、2 C、3 D、43. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A、1 B、2 C、3 D、43. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )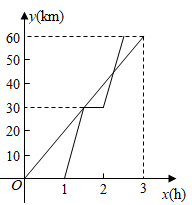 A、15km B、16km C、44km D、45km4. 某物体在力 的作用下,沿力的方向移动的距离为 ,力对物体所做的功 与 的对应关系如图所示,则下列结论正确的是( )
A、15km B、16km C、44km D、45km4. 某物体在力 的作用下,沿力的方向移动的距离为 ,力对物体所做的功 与 的对应关系如图所示,则下列结论正确的是( ) A、 B、 C、 D、5. 某气球内充满了一定质量 的气体,当温度不变时,气球内气体的气压 (单位: )是气体体积 (单位: )的反比例函数: ,能够反映两个变量 和 函数关系的图象是( )A、
A、 B、 C、 D、5. 某气球内充满了一定质量 的气体,当温度不变时,气球内气体的气压 (单位: )是气体体积 (单位: )的反比例函数: ,能够反映两个变量 和 函数关系的图象是( )A、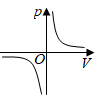 B、
B、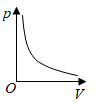 C、
C、 D、
D、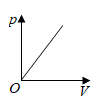 6. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )
6. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )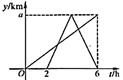 A、 B、 C、 D、7. 如图,在边长为4的菱形ABCD中,∠A=60°,点P从点A出发,沿路线A→B→C→D运动.设P点经过的路程为x,以点A,D,P为顶点的三角形的面积为y,则下列图象能反映y与x的函数关系的是( )
A、 B、 C、 D、7. 如图,在边长为4的菱形ABCD中,∠A=60°,点P从点A出发,沿路线A→B→C→D运动.设P点经过的路程为x,以点A,D,P为顶点的三角形的面积为y,则下列图象能反映y与x的函数关系的是( ) A、
A、 B、
B、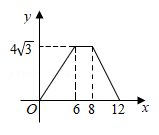 C、
C、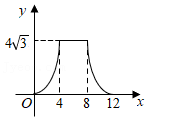 D、
D、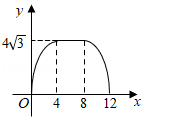 8. 如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是( )
8. 如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是( )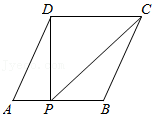 A、
A、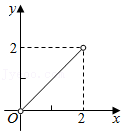 B、
B、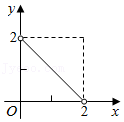 C、
C、 D、
D、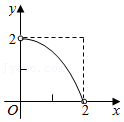 9. 已知A、B两点的坐标分别为(3,﹣4)、(0,﹣2),线段AB上有一动点M(m,n),过点M作x轴的平行线交抛物线y=a(x﹣1)2+2于P(x1 , y1)、Q(x2 , y2)两点.若x1<m≤x2 , 则a的取值范围为( )A、﹣4≤a<﹣ B、﹣4≤a≤﹣ C、﹣ ≤a<0 D、﹣ <a<010. 一对变量满足如图的函数关系.设计以下问题情境:
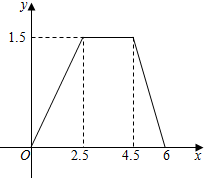
9. 已知A、B两点的坐标分别为(3,﹣4)、(0,﹣2),线段AB上有一动点M(m,n),过点M作x轴的平行线交抛物线y=a(x﹣1)2+2于P(x1 , y1)、Q(x2 , y2)两点.若x1<m≤x2 , 则a的取值范围为( )A、﹣4≤a<﹣ B、﹣4≤a≤﹣ C、﹣ ≤a<0 D、﹣ <a<010. 一对变量满足如图的函数关系.设计以下问题情境:①小明从家骑车以600米/分的速度匀速骑了2.5分钟,在原地停留了2分钟,然后以1000米/分的速度匀速骑回家.设所用时间为x分钟;②有一个容积为1.5升的开口空瓶,小张以0.6升/秒的速度匀速向这个空瓶注水,注满后停止,再以1升/秒的速度匀速倒空瓶中的水.设所用时间为x秒,瓶内水的体积为y升;③在矩形ABCD中,AB=2,BC=1.5,△ABP的面积为y.其中,符合图中函数关系的情境个数为( )
 A、3 B、2 C、1 D、011. 为规范市场秩序、保障民生工程,监管部门对某一商品的价格持续监控.该商品的价格 (元/件)随时间t(天)的变化如图所示,设 (元/件)表示从第1天到第t天该商品的平均价格,则 随t变化的图象大致是( )
A、3 B、2 C、1 D、011. 为规范市场秩序、保障民生工程,监管部门对某一商品的价格持续监控.该商品的价格 (元/件)随时间t(天)的变化如图所示,设 (元/件)表示从第1天到第t天该商品的平均价格,则 随t变化的图象大致是( )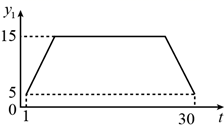 A、
A、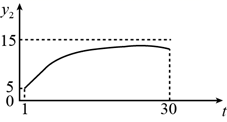 B、
B、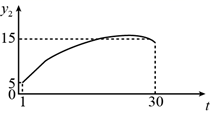 C、
C、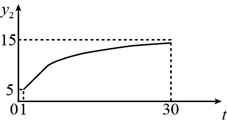 D、
D、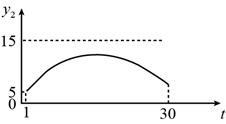 12. 函数 中,自变量 的取值范围是( )A、 B、 且 C、 D、 且13. 如图,菱形 的顶点分别在反比例函数 和 的图象上,若 ,则 的值为( )
12. 函数 中,自变量 的取值范围是( )A、 B、 且 C、 D、 且13. 如图,菱形 的顶点分别在反比例函数 和 的图象上,若 ,则 的值为( )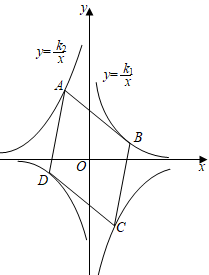 A、 B、 C、 D、14. 小风在1000米中长跑训练时,已跑路程x(米)与所用时间t(秒)之间的函数图象如图所示,下列说法错误的是( )
A、 B、 C、 D、14. 小风在1000米中长跑训练时,已跑路程x(米)与所用时间t(秒)之间的函数图象如图所示,下列说法错误的是( )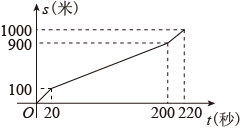 A、小风的成绩是220秒 B、小风最后冲刺阶段的速度是5米/秒 C、小风第一阶段与最后冲刺阶段速度相等 D、小风的平均速度是4米/秒15. 如图1,矩形 中,点 为 的中点,点 沿 从点 运动到点 ,设 , 两点间的距离为 , ,图2是点 运动时 随 变化的关系图象,则 的长为( )
A、小风的成绩是220秒 B、小风最后冲刺阶段的速度是5米/秒 C、小风第一阶段与最后冲刺阶段速度相等 D、小风的平均速度是4米/秒15. 如图1,矩形 中,点 为 的中点,点 沿 从点 运动到点 ,设 , 两点间的距离为 , ,图2是点 运动时 随 变化的关系图象,则 的长为( )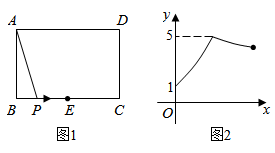 A、4 B、5 C、6 D、7
A、4 B、5 C、6 D、7二、填空题
-
16. 某种产品今年的年产量是20t,计划今后两年增加产量.如果每年的产量都比上一年增加x倍,两年后这种产品的产量y与x之间的函数表达式是 .17. 一个用电器的电阻是可调节的,其调节范围为:110~220Ω.已知电压为220ᴠ,这个用电器的功率P的范围是: w.(P表示功率,R表示电阻,U表示电压,三者关系式为:P·R=U²)18. 下表中记录了一次试验中时间和温度的数据.
时间/分钟
0
5
10
15
20
25
温度/℃
10
25
40
55
70
85
若温度的变化是均匀的,则14分钟时的温度是℃.
19. 育红学校七年级学生步行到郊外旅行.七(1)班出发1h后,七(2)班才出发,同时七(2)班派一名联络员骑自行车在两班队伍之间进行联络,联络员和七(1)班的距离s(km)与七(2)班行进时间t(h)的函数关系图象如图所示.若已知联络员用了 第一次返回到自己班级,则七(2)班需要 h才能追上七(1)班.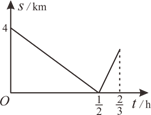 20. 以初速度v(单位:m/s)从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=vt﹣4.9t2.现将某弹性小球从地面竖直向上抛出,初速度为v1 , 经过时间t1落回地面,运动过程中小球的最大高度为h1(如图1);小球落地后,竖直向上弹起,初速度为v2 , 经过时间t2落回地面,运动过程中小球的最大高度为h2(如图2).若h1=2h2 , 则t1:t2=.
20. 以初速度v(单位:m/s)从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=vt﹣4.9t2.现将某弹性小球从地面竖直向上抛出,初速度为v1 , 经过时间t1落回地面,运动过程中小球的最大高度为h1(如图1);小球落地后,竖直向上弹起,初速度为v2 , 经过时间t2落回地面,运动过程中小球的最大高度为h2(如图2).若h1=2h2 , 则t1:t2=. 21. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.
21. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.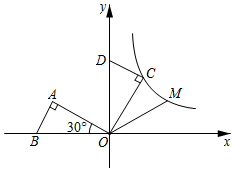 22. 我们规定:若 ,则 .例如 ,则 .已知 ,且 ,则 的最大值是.23. 已知函数y= ,若y=2,则x=.24. 如图,A,B两点的坐标分别为A(4,3),B(0,﹣3),在x轴上找一点P,使线段PA+PB的值最小,则点P的坐标是 .
22. 我们规定:若 ,则 .例如 ,则 .已知 ,且 ,则 的最大值是.23. 已知函数y= ,若y=2,则x=.24. 如图,A,B两点的坐标分别为A(4,3),B(0,﹣3),在x轴上找一点P,使线段PA+PB的值最小,则点P的坐标是 .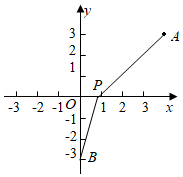 25. 如图,直线 与反比例函数 的图象交于A,B两点,与x轴交于点C,且 ,连接OA.已知 的面积为12,则k的值为.
25. 如图,直线 与反比例函数 的图象交于A,B两点,与x轴交于点C,且 ,连接OA.已知 的面积为12,则k的值为.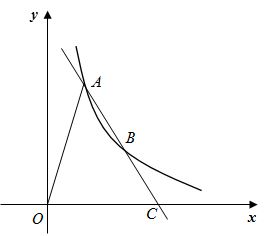 26. 如图,一次函数 与反比例数 的图象交于A,B两点,点M在以 为圆心,半径为1的 上,N是 的中点,已知 长的最大值为 ,则k的值是.
26. 如图,一次函数 与反比例数 的图象交于A,B两点,点M在以 为圆心,半径为1的 上,N是 的中点,已知 长的最大值为 ,则k的值是.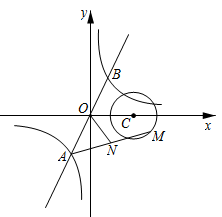 27. 从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度 (单位: )与它距离喷头的水平距离 (单位: )之间满足函数关系式 ,喷出水珠的最大高度是 .
27. 从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度 (单位: )与它距离喷头的水平距离 (单位: )之间满足函数关系式 ,喷出水珠的最大高度是 .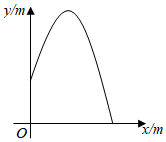 28. 如图,在同一平面直角坐标系中,直线l1:y x 与直线l2:y=kx+3相交于点A,则方程组 的解为 .
28. 如图,在同一平面直角坐标系中,直线l1:y x 与直线l2:y=kx+3相交于点A,则方程组 的解为 .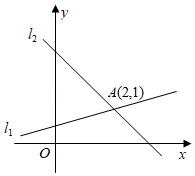 29. 如图(1),△ABC和△A′B′C′是两个边长不相等的等边三角形,点B′、C′、B、C都在直线l上,△ABC固定不动,将△A′B′C′在直线l上自左向右平移.开始时,点C′与点B重合,当点B′移动到与点C重合时停止.设△A′B′C′移动的距离为x,两个三角形重叠部分的面积为y,y与x之间的函数关系如图(2)所示,则△ABC的边长是.
29. 如图(1),△ABC和△A′B′C′是两个边长不相等的等边三角形,点B′、C′、B、C都在直线l上,△ABC固定不动,将△A′B′C′在直线l上自左向右平移.开始时,点C′与点B重合,当点B′移动到与点C重合时停止.设△A′B′C′移动的距离为x,两个三角形重叠部分的面积为y,y与x之间的函数关系如图(2)所示,则△ABC的边长是.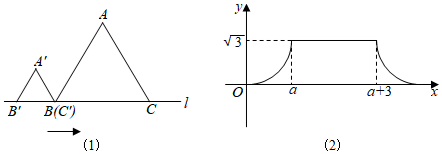 30. 春耕期间,市农资公司连续8天调进一批化肥,并在开始调进化肥的第七天开始销售.若进货期间每天调进化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个公司的化肥存量s(单位:吨)与时间t(单位:天)之间的函数关系如图所示,则该公司这次化肥销售活动(从开始进货到销售完毕)所用的时间是天.
30. 春耕期间,市农资公司连续8天调进一批化肥,并在开始调进化肥的第七天开始销售.若进货期间每天调进化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个公司的化肥存量s(单位:吨)与时间t(单位:天)之间的函数关系如图所示,则该公司这次化肥销售活动(从开始进货到销售完毕)所用的时间是天.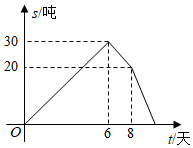 31. 如图所示:是一个运算程序示意图,若第一次输入1,则输出的结果是;
31. 如图所示:是一个运算程序示意图,若第一次输入1,则输出的结果是;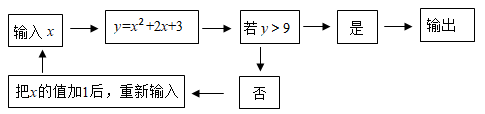 32. 如图1,菱形 的对角线 与 相交于点O,P、Q两点同时从O点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P的运动路线为 ,点Q的运动路线为 .设运动的时间为x秒,P、Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,当点P在 段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为厘米.
32. 如图1,菱形 的对角线 与 相交于点O,P、Q两点同时从O点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P的运动路线为 ,点Q的运动路线为 .设运动的时间为x秒,P、Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,当点P在 段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为厘米.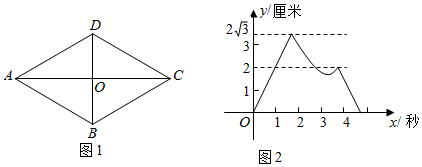 33. 若 ,且 ,则 的取值范围为.
33. 若 ,且 ,则 的取值范围为.